4.7. Изменения коэффициентов целевой функции

Предположим, что ограничения неизменны, а изменяются только коэффициенты це­левой функции. Тогда с геометрической точки зрения меняется только угол наклона прямой целевой функции. Что при этом происходит, мы уже наблюдали в разделе 4.3. На рис. 4.5 все данные модели Oak Products остались прежними, лишь удельный доход для стульев Mate возрос с $40 до $80 в расчете на один стул. В результате данного изменения изменился угол наклона прямой целевой функции, поэтому оптимальным стало новое угловое решение.

Экспериментируя с коэффициентами целевой функции модели Oak Products в про­грамме GLP, можно заметить, что некоторые изменения коэффициентов не приводят к изменению оптимального решения, несмотря на то, что прямая целевой функции име­ет другой угол наклона. Например, заменим целевую функцию 56С+ 40М новой функци­ей 56С + 48М. Как показано на рис. 4.4, решением для исходной целевой функции явля­лась пара значений С = 130, М = 60. В новой целевой функции переменной М соответст­вует более высокая удельная прибыль. Поэтому можно ожидать, что новое оптимальное решение будет предусматривать производство большего количества М. Поскольку их прибыльность возросла. Однако, как свидетельствуют представленные на рис. 4.10 ре­зультаты анализа новой модели программой GLP, этого не произошло. Оптимальные значения С и М не изменились, вновь было получено то же самое решение.

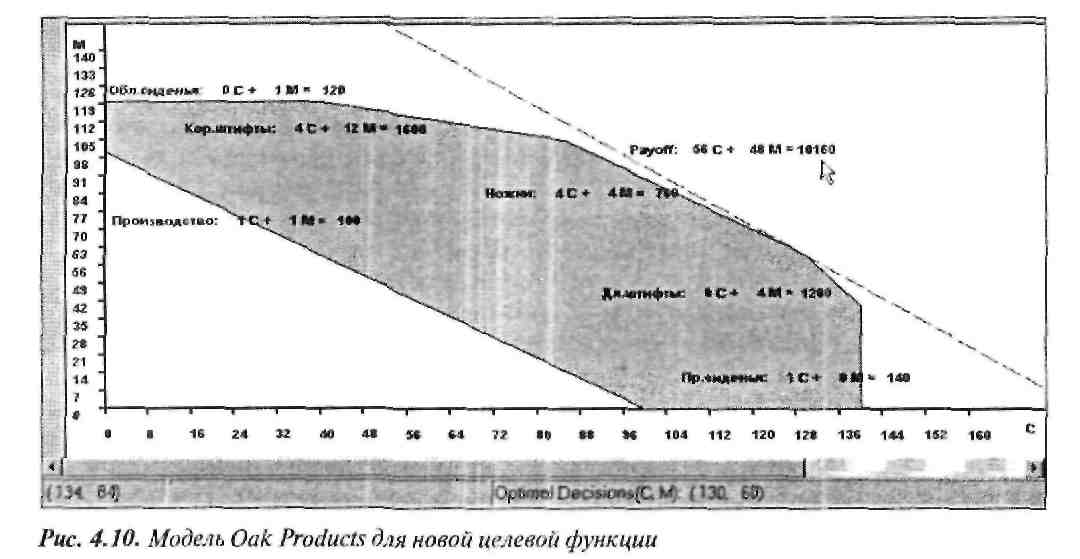
Совет. Если щелкнуть правой кнопкой мыши на линии целевой функции поблизости точки ее пересечения с одной из осей, а затем перетащить линию мышью, GLP будет поворачивать линию целевой функции вокруг точки пересечения с другой осью. Это позволяет непосредст­венно увидеть на графике связь между углом наклона линии целевой функции, угловыми точ­ками и перемещениями оптимального решения из одной угловой точки в другую при измене­нии угла наклона линии целевой функции.

Очевидно, что отрицательный наклон линий, связанных с каждой из трех рассмот­ренных целевых функций (рис. 4.4, 4.5 и 4.10), уменьшается по мере увеличения при­быльности М по отношению к С (т.е. при возрастании значения отношения коэффици­ента при М к коэффициенту при С). Однако, хотя целевые функции 56С+40М и 56С + 48М имеют разные углы наклона, эти углы недостаточно различны, чтобы полу­чить новое решение. Для обеих целевых функций оптимальное решение одно и то же: С = 130, М = 60. С другой стороны, поскольку коэффициент целевой функции изменил­ся, оптимальное значение целевой функции изменится, что и показано на трех указан­ных рисунках. Подведем итог.

| Изменение коэффициентов целевой функции приводит к изменению утла наклона прямой целевой функции. Это может отразиться (а может и не отразиться) на опти­мальном решении.

Сравнивая три вышеупомянутых рисунка, можно сделать вывод, что, если значение отношения коэффициента при М к коэффициенту при С равно 1, прямая целевой функ­ции будет иметь тот же наклон, что и линия ограничения для ножек. Более того, как только значение данного отношения превысит 1, новое оптимальное решение (рис. 4.5) станет предпочтительней, чем решение, показанное на рис. 4.4. Если же значение этого отношения равно !, прямая целевой функции параллельна линии ограничения для но­жек, и программам GLP или Поиск решения будет безразлично, какое из угловых реше­ний (на рис. 4.4 или на рис. 4.5) выбрать, поскольку оба решения дают одинаковое зна­чение целевой функции.

Напоминаем, что если в модели с двумя переменными прямая целевой функции парал­лельна прямой какого-либо ограничения (в нашем случае это ограничение для ножек), то су­ществует два оптимальных угловых решения: текущее решение, находящееся на пересечении ограничения для ножек и ограничения для длинных штифтов, и второе решение, задаваемое пересечением ограничения для ножек и ограничения для коротких штифтов. Более того в та­ком случае все точки прямой ограничения для ножек, находящиеся между этими угловыми точками, также являются оптимальными. В ситуации, когда имеется несколько наборов оп­тимальных значений переменных решения, дающих одинаковое значение целевой функции, используется термин множественные (альтернативные) оптимальные решения.

Если задача ЛП имеет более одного оптимального решения, т.е. существуют множест­венные оптимальные решения, то этих оптимальных решений бесконечно много.

Рассмотрим теперь результаты применения средства Поиск решения для этих трех различных целевых функций, чтобы разобраться, как интерпретировать информацию, содержащуюся в отчете по устойчивости, генерируемом этим средством. На рис 4.11 представлена таблица модели Oak Products, в которой показано оптимальное решение за­дачи ЛП из главы 3, только вместо отчета о результатах был выбран отчет по устойчиво­сти. Отчет по устойчивости располагается на отдельном рабочем листе, на котором убра­ны линии сетки (см. рис. 4.11). Вторая строка верхней части отчета, озаглавленной Из­меняемые ячейки, содержит значение 40 в столбце Целевой коэффициент (для стульев Mate), а Допустимое увеличение дня данного коэффициента равно 16. Это означает, что если остальные данные модели останутся неизменными, то, увеличив коэффициент це­левой функции для стульев Mate (т.е. удельный доход в расчете на единицу продукции) не более чем на 16, мы получим то же самое оптимальное решение задачи ЛП, что и в ис­ходном случае; если же прирост составит более 16, текущее решение, полученное с по­мощью Поиск решения, уже не будет оптимальным. Почему так происходит?

Замечание. При составлении отчета по устойчивости Поиск решения для каждой из ячеек левых частей ограничений просматривает таблицу модели справа налево, пока не найдет заго­ловок строки (если таковой существует) в строке данного ограничения. Затем программа про­сматривает таблиц}' вверх от рассматриваемой ячейки, пока не обнаружит заголовок столбца (если он существует) в столбце данного ограничения. Эти два заголовка соединяются и образу­ют заголовок, соответствующий данному ограничению в отчете по устойчивости. Аналогич­ный процесс в отчете по устойчивости выполняется и с целью создания заголовков для ячеек переменных решения. Правильный выбор и размещение заголовков в табличном представлении модели ЛП позволяют создать информативные заголовки в отчете по устойчивости.

Если прирост коэффициента целевой функции при переменной М:

...меньше 16, то значение отношения коэффициента при М к коэффициенту при С бу­дет меньше 1; как мы уже видели ранее в программе GLP, такого изменения целевой функции недостаточно, чтобы решение сместилось из текущей угловой точки;

...больше 16, значение отношения коэффициента при М к коэффициенту при С будет больше 1; как следует из анализа, проведенного в GLP, такое изменение целевой функ­ции приведет к смещению решения из текущей угловой точки в другую угловую точку:

...равно 16, значение отношения коэффициента при М к коэффициенту при С будет равно 1; как следует из анализа, проведенного в GLP, это приведет к тому, что оба угло­вых решения будут давать одно и то же значение целевой функции, т.е. существуют мно­жественные оптимальные решения.

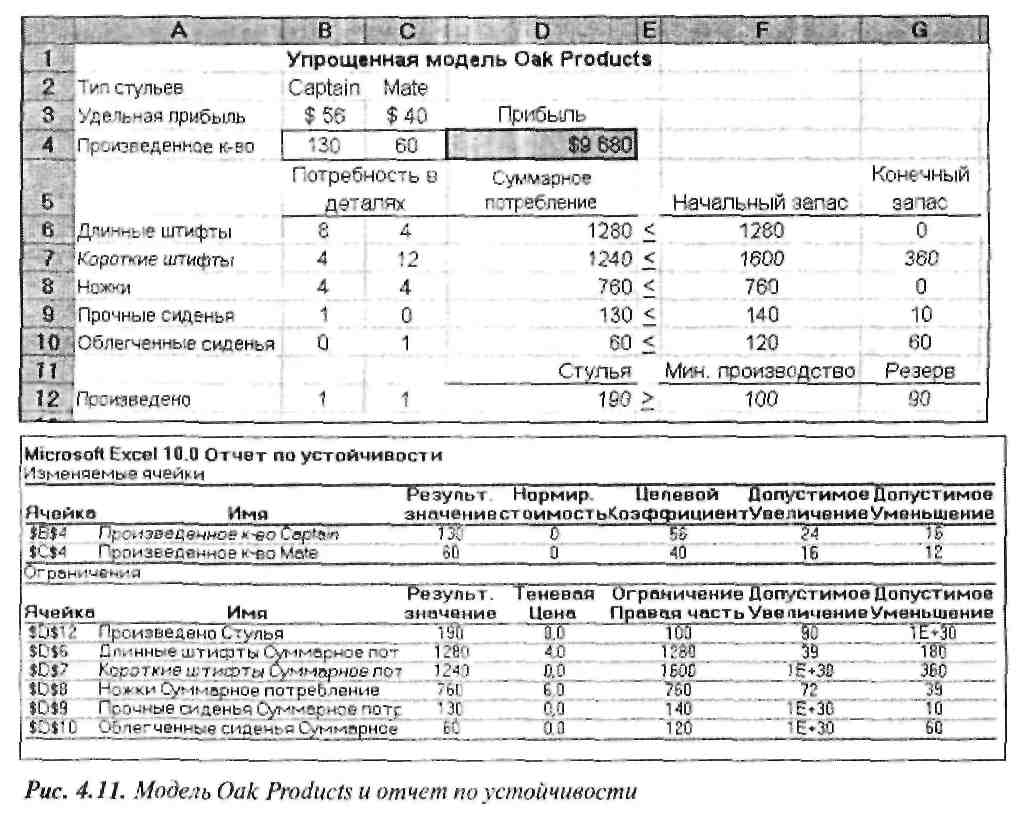
Аналогично, если остальные данные модели остаются неизменными, Допустимое уменьшение целевого коэффициента для стульев Captain, равного 56, составляет 16. Та­ким образом, чтобы значение отношения коэффициента при переменной М к коэффи­циенту при переменной С стало равным 1, нужно уменьшить значение данного коэффи­циента на 16, а это означает, что снижение коэффициента на меньшую величину не при­ведет к изменению текущего решения, предложенного средством Поиск решения.

Итак, значения Допустимое увеличение и Допустимое уменьшение в таблице Изме­няемые ячейки отчета по устойчивости показывают, на сколько можно изменить Целевой коэффициент при заданной переменной решения в целевой функции, оставив неизмен­ными остальные данные модели, чтобы при повторной оптимизации модели получить то же самое решение. Иными словами, диапазоны целевого коэффициента задают пределы изменений данного коэффициента (остальные данные остаются постоянными), которые не вызовут изменений оптимального решения. Программа GLP позволяет увидеть, куда пере­местится оптимальное решение задачи ЛП при изменении целевого коэффициента, выхо­дящего за пределы указанного диапазона. В отчете по устойчивости средства Поиск реше­ния не содержится никакой информации о том, где будет находиться новое угловое реше­ние. Но отчет по устойчивости предоставляет информацию, пусть и ограниченную, для моделей ЛП произвольной размерности, в то время как визуальные возможности програм­мы GLP ограничены моделями с двумя переменными решения. Подведем итог.²

Решение задачи ЛП может оказаться вырожденным, в таком случае перечисленные далее пункты нужно рассматривать как некое упрощение. Более глубоко проблема вырождения в моделях ЛП рассматривается в разделе 4.13.

1. Значения в столбцах Допустимое увеличение и Допустимое уменьшение раздела Изменяемые ячейки отчета по устойчивости показывают, на сколько можно уве­личить или уменьшить коэффициент при переменной в целевой функции, чтобы оптимальное решение (т.е. значения переменных решения) осталось неизменным, при условии, что остальные данные считаются фиксированными. При этом опти-мальное значение целевой функции может измениться.

2. Если величина изменения целевого коэффициента меньше допустимой, текущее оптимальное решение остается единственным.

3. Если коэффициент при переменной в целевой функции увеличить или уменьшить в точности на допустимую величину, появится альтернативное оптимальное решение.

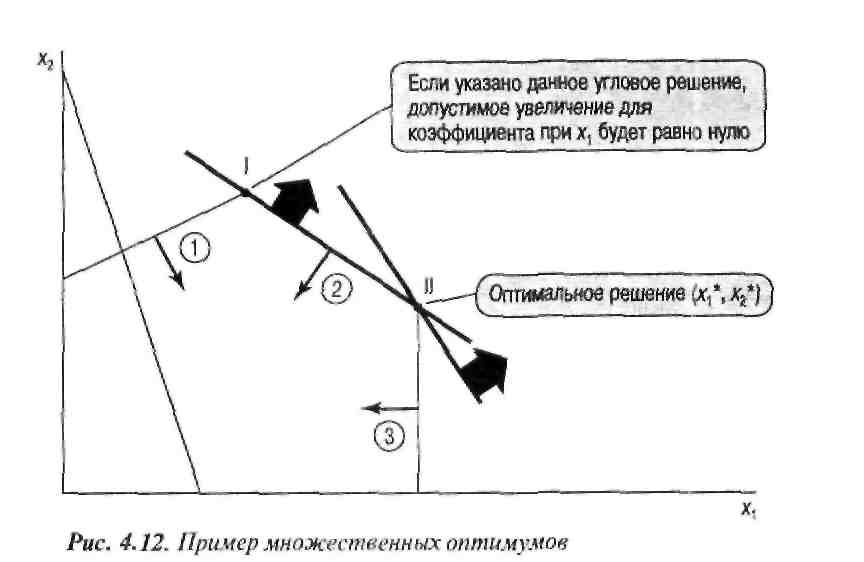
На основании отчета по устойчивости можно сделать еще один интересный вывод о решении : если для некоторой переменной из таблицы Изменяемые ячейки в столбце Допустимое увеличение или Допустимое уменьшение содержится нулевое значение, значит, для данной модели существует по крайней мере одна альтернативная угловая точка оптимального решения. Более того, если альтернативное оптимальное решение существу­ет, обязательно появится такое нулевое значение. Это правило проиллюстрировано на рис. 4.12, где изображена гипотетическая линейная модель максимизации с двумя пере­менными и тремя ограничениями-неравенствами. Прямая целевой функции параллельна прямой второго ограничения (помеченного цифрой 2). Видно, что угловые точки 1 и 11 являются альтернативными оптимумами данной модели. Поскольку Поиск решения ис­пользует для оптимизации моделей ЛП метод, который просматривает угловые решения по очереди, программа укажет в качестве оптимального решения только одно из них, и отчет по устойчивости будет составлен только для этого углового решения. Предполо­жим, что с помощью средства Поиск решения найдено угловое решение I. Из представ­ленной на рис. 4.12 геометрической интерпретации модели следует, что любое увеличе­ние коэффициента при х1 изменит угол наклона прямой целевой функции, например, она приблизится к линии, нарисованной пунктиром, и единственным оптимальным ре­шением станет угловая точка II. Отчет по устойчивости укажет на это, проставив нулевое значение для х1 в столбце Допустимое увеличение.

Увеличивая в нашей модели коэффициент при переменной М (при фиксированном значении коэффициента при переменной С), в конце концов получим новое решение (рис. 4.5), в котором оптимальное значение М больше исходного решения. Этот результат вполне соответствует интуитивным соображениям, поскольку увеличение прибыльности М не должно приводить к снижению их выпуска! Данная ситуация иллюстрирует общее положение.

| В модели максимизации увеличение коэффициента при какой-либо переменной реше­ния (т.е. увеличение прибыльности деятельности, связанной с этой переменной) при условии постоянства остальных данных не может привести к снижению оптимального значения этой переменной (т.е. не снижает уровня данной деятельности).

' Более точно — о невырожденном решении.

При наличии в модели ЛП альтернативных оптимумов незначительные отличия в точности выполнения арифметических вычислений часто приводят к тому, что на одном компьютере Поиск решения находит одно оптимальное решение, а на другом — альтернативное угловое решение.

Ситуация для модели минимизации прямо противоположна. Поскольку в этом случае минимизируются общие затраты, то увеличение затрат на некую деятельность при неиз­менности остальных параметров не может привести к повышению оптимального уровня

данной деятельности. Еше одно общее положение выглядит следующим образом.

...

В модели минимизации увеличение коэффициента при какой-либо переменной реше­ния (т.е. увеличение затрат на деятельность, связанную с этой переменной) при посто­янстве остальных данных не может привести к увеличению оптимального значения \ этой переменной (т.е. не повышает уровень данной деятельности).