4.4. Графическое решение задачи минимизации

Мы рассмотрели графическое представление модели максимизации. Однако, как уже отмечалось в главе 3, многие реальные модели призваны решать задачи минимизации. Примером такой модели может служить модель компании Eastern Steel, рассмотренная в главе 3. Применение графического метода к моделям минимизации во многом анало­гично поиску максимума; единственное отличие заключается в том, что оптимизирующим направлением для прямой целевой функции является "спуск", а не "подъем''. В модели мак­симизации прямые целевой функции зачастую представляют собой изолинии прибыли. В моделях минимизации прямые целевой функции обычно являются изолиниями затрат. В модели минимизации необходимо найти угловую точку допустимой области, лежащую на самой нижней прямой целевой функции, пересекающей допустимую область. В каче­стве примера используем программу GLP для поиска решения следующей простой зада­чи минимизации с двумя переменными решения х1 и х2.

Минимизировать

при ограничениях

На рис. 4.7 представлена GLP-версия данного примера. Эту модель можно оптимизи­ровать, сдвинув прямую целевой функции на юго-запад (или щелкнув на кнопке Auto Min (Автоминимум), на которой изображена стрелка, направленная вниз).

Заметим, что оптимальное решение лежит на оси х2 на пересечении прямой третьего ог­раничения и прямой ограничения неотрицательности. Ось х, задается уравнением х1 = 0. Таким образом, оптимальное решение определяется системой двух уравнений х2=0

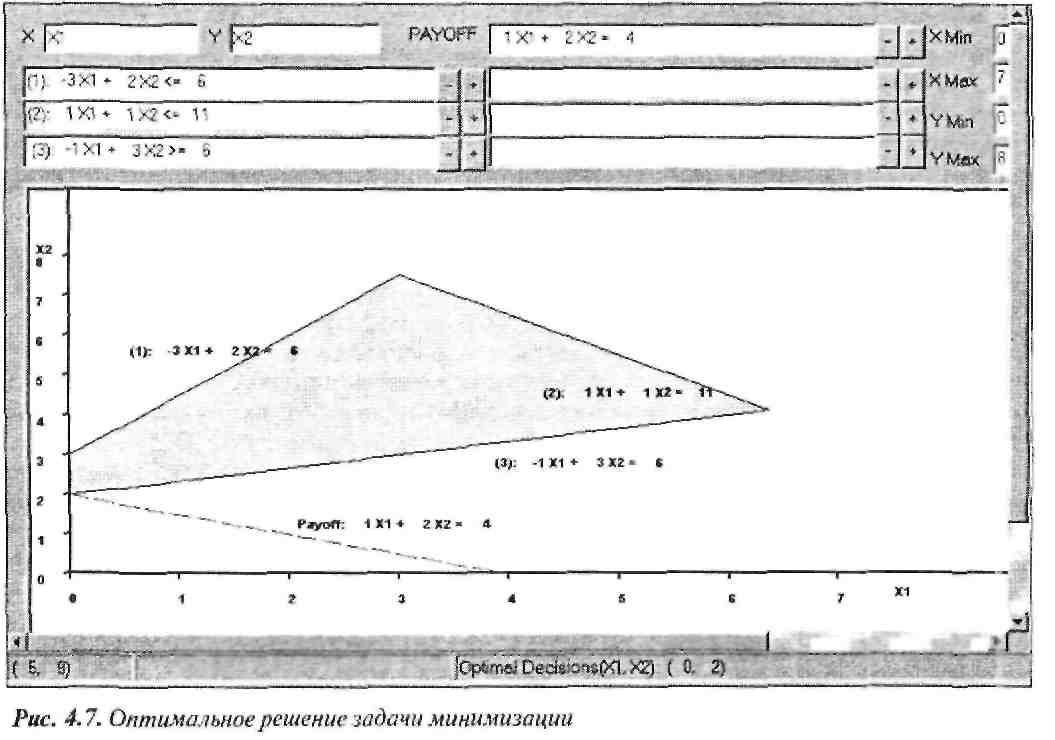
как показано на рис. 4.7

откуда следует х = 0 и х1 = 2 ,

стрирует, что если двигать прямую целевой функции в оптимизирующем направлении, гра­фический анализ модели минимизации идентичен анализу модели максимизации.

Следует сделать одно предостережение. Студенты зачастую попадают в ловушку, счи­тая, что решение задачи максимизации всегда находится в наиболее удаленном от начала координат углу, а оптимальное решение задачи минимизации — в начале координат, ес­ли данная точка входит в допустимую область, в противном случае (когда начало коорди­нат не является допустимым решением) — в углу, ближайшем к началу координат. Такие суждения могут оказаться неверными. Они основаны на впечатлении, что подъем целевой функции всегда направлен строго на северо-восток от начала координат, а спуска — строго на юго-запад к началу координат. На самом деле не существует всеобщей связи между подъемом или спуском целевой функции и началом координат.

4.5. Неограниченные и недопустимые модели

Итак, мы рассмотрели геометрическое представление оптимизационных моделей ЛП с двумя переменными решения. Приведенные геометрические примеры позволили сде­лать важное заключение: если задача имеет оптимальное решение, всегда хотя бы одно решение будет находиться в угловой точке области допустимых решений. Теперь рас­смотрим, в каких случаях задача ЛП не имеет оптимального решения. Вновь воспользу­емся геометрическим представлением.

Неограниченные модели

Вернемся к графическому изображению модели Oak Products на рис. 4.3, однако те­перь изменим ее, предположив, что все ограничения, кроме (4.4) и (4.7), по невнима­тельности были пропущены. Графическое представление новой модели в программе GLP показано на рис. 4.8. Как видим, теперь допустимая область неограниченно простирается в восточном направлении, поэтому можно сколь угодно далеко двигать линию целевой функции в этом направлении. Щелчок на кнопке Auto Max приведет к появлению сооб­щения о неограниченности допустимой области, показанного на рис. 4.8.

Поскольку для данной конкретной модели оптимизирующим направлением является восточное, можно найти допустимое решение со сколь угодно большими значениями целе­вой функции. Иными словами, можно получить прибыль, стремящуюся к бесконечности. У такой модели нет решения, поскольку целевая функция неограничена. Таким образом, для любого набора допустимых значений переменных решения можно найти другие допусти­мые значения, которые улучшат значение целевой функции. Модели такого типа называ­ются неограниченными моделями. Неограниченная модель— это аномалия. Такая модель может получиться, если, как в представленном на рис. 4.8 случае, одно или несколько огра­ничений были пропущены или были допущены ошибки при вводе неравенств, задающих ограничения. В реальной жизни никому еще не удалось найти способ получения бесконеч­ной прибыли, поэтому можно не сомневаться, что корректно сформулированная и пра­вильно введенная модель не будет неограниченной. Заметим, что модель с неограниченной допустимой областью не обязательно является неограниченной моделью. Например, если на рис. 4.8 для другой целевой функции увеличение ее значений происходит при движении в северо-западном направлении, такая задача будет иметь решение.

Недопустимые модели

Как уже отмечалось в главе 3, существует другой тип аномалии, которой необходимо избегать в линейном программировании. Это недопустимость {несогласованность) огра­ничений. Этим термином обозначаются модели, множество допустимых значений кото­рых пусто, т.е. ни одна комбинация значений переменных решения не удовлетворяет всем ограничениям одновременно. Приведем пример недопустимой модели линейного программирования.

Максимизировать при ограничениях

Графическое представление области решений для данной модели ЛП показано на рис. 4.9. Нетрудно убедиться, что не существует пары значений Е и F, соответствующей всем ограничениям.

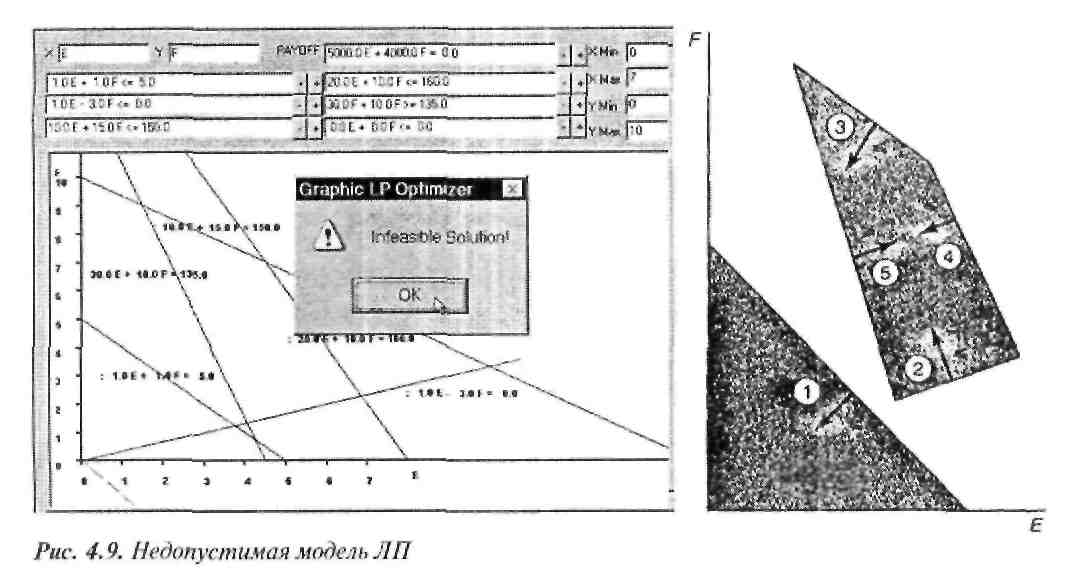
Как следует из рис. 4.9, отсутствие допустимых решений зависит только от ограничений и не зависит от целевой функции. Очевидно, что недопустимая задача Л П не имеет решений, но аномалии такого рода не возникают в корректно разработанных моделях. Иными слова­ми, недопустимость в правильно поставленной задаче всегда означает, что модель непра­вильно описана: возможно, ошибки могут заключаться в том, что ограничений слишком много или неправильны некоторые неравенства ограничений. Подведем итог.

Каждая задача линейного программирования относится к одной из трех взаимоисклю-чающих категорий.

1. Задача имеет оптимальное решение.

2. Оптимального решения нет, поскольку модель является неограниченной.

3. Оптимального решения нет, поскольку модель не имеет допустимых решений.

На практике корректно сформулированная задача ЛП всегда имеет решение. Неогра­ниченные и недопустимые модели являются результатом ошибок при формировании мо­дели или вводе ограничений в Excel либо GLP.