4.3. Крайние точки и оптимальные решения

Таким образом, решение задачи ЛП Oak Products находится в угловой точке допусти­мой области, а именно — в вершине угла, образованного при пересечении линий ограни­чений для длинных штифтов и ножек. В линейном программировании углы допустимой области называются крайними точками. В дальнейшем мы будем использовать оба тер­мина, угловые точки и крайние точки, вкладывая в них один и тот же смысл.

Чтобы понять, насколько важны крайние точки, рассмотрим различные линейные целевые функции на одном и том же множестве ограничений и решим полученные зада-чи ЛП. Предположим, что компания Oak Products изменит цену на стулья типа Mate, и удельный доход в расчете на один стул будет составлять не $40, а $80. Посмотрим .: по­мощью программы GLP, как это изменение целевой функции повлияет на решение зада­чи ЛП. Во-первых, поскольку изменению подверглась только целевая функция, допус-тимая область останется неизменной. Изменится только целевая функция, т.е. линия, соответствующая целевой функции, на графике будет иметь другой наклон. В окне GLP в поле ввода Payoff введем коэффициент 80 для переменной М и щелкнем на кнопке Auto Max, чтобы повторно оптимизировать модель. В результате получим оптимальное решение, представленное на рис. 4.5.

Как показано на рисунке, новую оптимальную точку определяют другие лимитирую-шие ограничения. Теперь лимитирующими являются ограничения для коротких штиф­тов и для ножек, в то время как в предыдущем случае лимитирующими были ограниче­ния для длинных штифтов и ножек. Таким образом, изменение угла наклона целевой

функции привело к тому, что оптимальное решение сместилось из предыдущей угловой точки в новую угловую точку. Как можно было предвидеть, новая структура цен, в кото­рой возросла относительная прибыльность стульев Mate, привела к новому оптимально­му производственному плану, в котором количество стульев Captain сократилось со 130 до 85, а количество стульев Mate возросло с 60 до 105.

Можете самостоятельно провести эксперименты с программой GLP, чтобы убедить­ся: независимо от того, как будет изменяться целевая функция (оставаясь линейной), оп­тимальным решением будет угловая точка. Можно изменить и множество ограничений, оптимальное решение все равно будет угловым, пока уравнения модели остаются линей­ными. Это очень важное наблюдение, дополнительные подтверждения которого рас­сматриваются ниже.

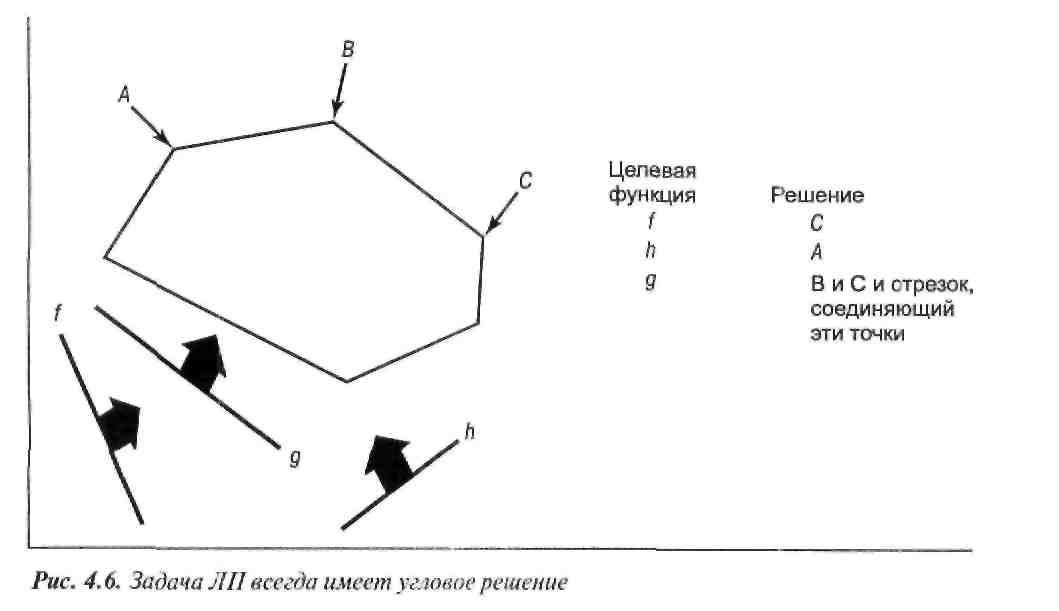
На рис. 4.6 изображено произвольное шестистороннее множество ограничений и прямые трех различных целевых функций, обозначенных f, g и И. Для каждой целевой функции стрелка указывает направление, в котором оптимизируется соответствующая целевая функция. В каждом случае оптимальное решение окажется в некой в угловой точке. Целевая функция g на рис. 4.6 иллюстрирует интересный случай, когда оптималь­ная прямая целевой функции совпадает с одной из линий ограничений, составляющих границу допустимой области. Это может получиться только тогда, когда прямая целевой функции имеет тот же угол наклона, что и линия ограничения. В таком случае будет бесконечно много оптимальных решений, а именно — угловые точки В, С и все заключенные между ними точки границы допустимой области. Такие решения называются множественными опти­мумами. Однако даже в том случае, когда единственного оптимального значения нет, по-прежнему верно утверждение, что существует оптимальное угловое решение (фактически их два). Данная геометрическая иллюстрация подтверждает важный факт, справедливый для моделей ЛП с произвольным числом переменных решения.

Если модель ЛП имеет оптимальное решение, всегда существует по крайней мере одно угловое решение.