4.10. Анализ чувствительности в действии

Мы уже рассматривали модель компании Eastern Steel в разделе ЗЛО. Напомним по­становку задачи. Для выплавки легированной стали смешивается руда, поступающая с 4 месторождений. Каждая руда содержит три основных элемента, обозначенных для простоты А, В и С. их минимальное содержание в рудной смеси должно быть не ниже оп­ределенных пороговых значений. Компания платит разную цену за тонну руды с различ­ных месторождений. Минимизирующая затраты рудная смесь получается с помощью решения приведенной ниже задачи ЛП, где 7; — процентное содержание руды с место­рождения i в тонне смеси. Решение данной задачи, найденное средством Поиск реше­ния, а также отчет по устойчивости для оптимального решения показаны на рис. 4.26.

Минимизировать при ограничениях

Нормированная стоимость

К настоящему моменту мы объяснили смысл всех элементов отчета по устойчивости за исключением данных в столбце Нормированная стоимость. Эти данные можно ин­терпретировать следующими способами.⁹

1. Нормированная стоимость определенной переменной решения определяется как ве­личина, на которую нужно изменить коэффициент при данной переменной в целе­вой функции, чтобы оптимальное значение этой переменной стало положитель­ным.¹⁰ Таким образом, если переменная решения в точке оптимальности положи­тельна, нормированная стоимость для нее равна нулю (см. переменные решения задачи Oak Products на рис. 4.5, 4.15 и 4.17). Если же оптимальное значение некой переменной решения равно 0, то нормированная стоимость в строке, соответствую­щей данной переменной, равна значению в столбцах Допустимое увеличение или Допустимое уменьшение (одно из этих значений будет бесконечным, а второе равно нормированной стоимости). Например, переменная решения Т₄ в модели на рис. 4.26 в точке оптимальности имеет нулевое значение. Нормированной стоимо­стью переменной Т₄ является величина, на которую необходимо уменьшить соответ­ствующие ей удельные затраты (коэффициент при Т₄ в целевой функции), чтобы по­лучить оптимальное решение, содержащее положительное значение Т₄. Именно это значение находится напротив переменной Т₄ в столбце Допустимое уменьшение. В рассматриваемом случае при любом увеличении коэффициента при Т₄ (что делает Т₄ более дорогой) оптимальное значение Т₄ будет оставаться равным 0.

2. Альтернативный способ интерпретации нормированной стоимости переменной решения, текущее оптимальное значение которой равно 0, — использовать коэф­фициент (удельной величины) уменьшения значения целевой функции при введе­нии данной переменной в изначально оптимальное решение. Следовательно, нужно отказаться от предложенного средством Поиск решения нулевого значения и заставить данную переменную принимать положительные значения. Если в оп­тимальном решении Т₄ = 0, то оптимальная стоимость тонны смеси возрастет, ес­ли искать оптимальное решение для модели с дополнительным ограничением, скажем, Т₄ = 0,1. Этот коэффициент возрастания оптимальной стоимости при ус­ловии, что Т₄ должна принимать положительные значения, и будет нормирован­ной стоимостью Т₄.

Напомним, что теневая цена ограничения — это коэффициент изменения оптималь­ного значения целевой функции при увеличении значений правой части данного ограни­чения. Поскольку в рассматриваемой модели Т₄ — 0, ограничение неотрицательности для Т₄ является лимитирующим. Если мы заставляем Т₄ принимать положительные значения, это то же самое, что увеличивать правую часть ограничения неотрицательности. Отсюда следует еще одна эквивалентная интерпретация: для модели, содержащей условия неот­рицательности, нормированная стоимость является теневой ценой ограничения неотри­цательности для рассматриваемой переменной решения.

Это еще один пример, когда для корректной интерпретации результатов отчета необходимо удостове­риться, что данное оптимальное решение является невырожденным.

Это стандартное определение нормированной стоимости для невырожденного решения. К сожалению, даже при невырожденном решении в отчете по устойчивости в столбце Нормированная стоимость иногда появля­ется другая информация, которая может ввести в заблуждение. Пример рассматривается в разделе 4.12.

Дополнительные примеры различных интерпретаций нормированной стоимости можно найти в приведенном ниже диалоге, который должен показать, как информация отчета по устойчивости применяется в реальных ситуациях. Представьте себя на месте менеджера компании Eastern Steel, отвечающего за планирование производства. Вы за­даете вопросы, а разработчик модели вам отвечает.

МЕНЕДЖЕР. Прежде всего, что собой представляет решение нашей задачи?

РАЗРАБОТЧИК. Под решением я подразумеваю оптимальные значения переменных решения. Оп­тимальные значения записаны в ячейках ВЗ.ЕЗ рабочего листа модели и состав­ляют (округленно) 77 = 0,26, Т2 = 0,70, ТЗ = 0,04, Т4 = 0,00. При этом мини­мальная стоимость тонны смеси составляет $511, 11 (ячейка F4).

МЕНЕДЖЕР. Мне бы хотелось, чтобы стоимость тонны смеси не превышала $500. Нет ли способа добиться этого? Я вижу в таблице столбец под названием Излишек.

РАЗРАБОТЧИК. Если бы можно было найти более дешевую рудную смесь, удовлетворяющую огра­ничениям, Поиск решения нашел бы это решение. Столбец обозначен Излишек, но, вообще говоря, подразумевается "резерв или превышение" — для каждой си­туации выбирается более подходящее название. В данном случае в этом столбце показаны величины превышения ограничений.

МЕНЕДЖЕР. Может быть, мне удастся изменить эти ограничения. Превышение для ограничения по элементу А равно 0 (ячейка 16), а требование к минимальному содержанию этого элемента — 5 фунтов. Это означает, что в тонне смеси содержится ровно 5 фунтов элемента А. Поскольку превышение в ячейке 18 также равно нулю, тонна оптималь­ной смеси содержит ровно 30 фунтов элемента С. Однако в ячейке 17, соответствую-щей элементу В, я вижу превышение 31,67, таким образом, данное ограничение не яв­ляется лимитирующим, и мы добавляем в смесь лишнее количество В.

РАЗРАБОТЧИК. Да, это означает, что в оптимальной смеси требование к минимальному содер­жанию элемента В (100 фунтов) превышено на 31,67, и действительное содержа­ние его составляет 131,67 фунтов, что показано в ячейке F7.

МЕНЕДЖЕР. Возможно, удастся составить более дешевую смесь, используя меньше В За­чем нам более 131 фунта элемента В, если необходимо только 100 фунтов?

РАЗРАБОТЧИК. Это интересный вопрос. Оказалось, что тонна самой дешевой комбинации руд, удовлетворяющей требованиям по элементам А и С, содержит более 100 фунтов элемента В. Любая комбинация руд, содержащая меньше В, либо не будет содер­жать необходимого количества А и/или С, либо же будет стоить дороже, чем $511,11 за тонну. Иными словами, попытка сократить превышение по содержа­нию элемента В при условии соблюдения требований по элементам А и С приведет к повышению стоимости.

МЕНЕДЖЕР. Понятно. А как можно снизить общую стоимость тонны смеси до S500 или меньше?

РАЗРАБОТЧИК. Необходимо ослабить ограничения. В данном случае нужно ослабить требования к содержанию элементов А и С.

МЕНЕДЖЕР. Почему не к элементу В7

РАЗРАБОТЧИК. Потому что, пытаясь удовлетворить требования по элементам А и С с минималь-ными затратами, мы включили в смесь более 100 фунтов В, что превышает мини­мальное пороговое значение. Иными словами, требование к содержанию В не являет-ся лимитирующим. Если ослабить данное требование, задав меньшее пороговое зна­чение, например 98, оптимальная смесь будет иметь все тот же состав и стоимость. Таким образом, ослабление требования к содержанию элемента В ни­чего не даст. Чтобы изменить стоимость смеси, необходимо ослабить одно из ли­митирующих требований.

МЕНЕДЖЕР. Хорошо. Значит, я должен снизить требование к содержанию элемента А или С. Но какое именно и на сколько?

РАЗРАБОТЧИК. Для ответа на данный вопрос можно воспользоваться информацией, содержащей­ся в столбце Теневая цена отчета по устойчивости. Значение теневой цены по­казывает коэффициент изменения оптимального значения целевой функции при увеличении правой части ограничения. Поскольку мы хотим ослабить ограничение вида >=, нам нужно уменьшить значение правой части. Посмотрим на значение теневой цены ограничения по элементу А. Оно равно +44,44. Знак + означает, что при увеличении правой части данного ограничения оптимальное значение стоимо­сти повышается (т.е. ухудшается). Следовательно, при уменьшении значения правой части оптимальное значение целевой функции уменьшается. Это под­тверждает основанное на здравом смысле предположение, что при ослаблении требования к содержанию элемента А минимальная стоимость тонны смеси снизится. Теневая цена показывает, что она снижается на $44,44 при снижении требования к содержанию А в тонне смеси на 1 фунт.

МЕНЕДЖЕР. Итак, ослабить требование для элемента А значит снизить его с 5 фунтов до некоего меньшего значения. И теневая цена +44,44 показывает, что при каж­дом уменьшении данного требования на 1 фунт общая стоимость тонны смеси снижается на S44,44. Таким образом, если потребовать, чтобы смесь содержала только 4 фунта А на тонну вместо 5, стоимость тонны смеси снизится пример­но до S466.67, а это значительно меньше $500! Если же сократить требование лишь до 4,5 фунтов, удастся сэкономить более S22 ((1/2)х44,44), и суммарная стоимость все равно окажется меньше $500. Правильно?

РАЗРАБОТЧИК. В принципе, да. Вы взяли правильный коэффициент изменения, однако данное зна­чение коэффициента действует только в определенном интервале в окрестности исходного значения 5. А соответствующий интервал может не позволить проана­лизировать уменьшение правой части требования на целую единицу или даже на половину единицы. МЕНЕДЖЕР. Понятно. В столбце Допустимое уменьшение для ограничения элемента А стоит значение 0,25. Это означает, что можно анализировать только уменьше­ние правой части ограничения с 5 до 4,75. В этом случае экономия составит 0,25x$44,44 = $11,11, т.е. тонна смеси будет стоить ровно $500. Но что будет, если снизить требование несколько больше, скажем, до 4,5? Позволит ли это дополнительно снизить стоимость?

РАЗРАБОТЧИК. Вероятно, однако я не могу точно определить, на сколько, так как коэффициент изменения может стать другим при уменьшении требования более, чем на 0,25, иными словами, теневая цена может измениться.

МЕНЕДЖЕР. Теперь, чтобы убедиться, что я правильно все понял, попробую проанализировать потенциальную экономию при снижении требования к содержанию элемента С. Исходное значение правой части равно 30. Как видно из отчета по устойчивости, допустимое уменьшение составляет 7, следовательно, можно снизить данное требо­вание до 23. Соответствующая теневая цена +4,44. Это коэффициент экономии при снижении значения правой части. Таким образом, снизив данное требование до 23, можно сэкономить 7x4,44 = $31,08, что позволит сделать стоимость тонны смеси заметно ниже S500. Если снизить требование только на 2,5 фунта, можно приме­нить тот же коэффициент, следовательно, экономия составит 2,5x4,44 = $11,10, что позволит получить стоимость практически равную $500. Правильно?

РАЗРАБОТЧИК. Абсолютно.

МЕНЕДЖЕР. Итак, мы выяснили, что можно снизить стоимость тонны смеси до $500 путем снижения требования к содержанию элемента А до 4,75 фунтов в тонне или требования к элементу С до 27,5 фунтов в тонне. Теперь хотелось бы узнать, что будет, если снизить оба требования (к содержанию элементов А и С), воз­можно, на меньшее значение, но одновременно?

РАЗРАБОТЧИК. К сожалению, отчет по устойчивости не содержит информации, которая позволи­ла бы дать точный ответ на этот вопрос. При интерпретации теневой цены одного из ограничений необходимо сохранять неизменными остальные ограничения модели. Единственный способ ответить на вопрос, что будет при одновременном изменении нескольких правых частей, — это многократно решить задачу для различных значе­ний соответствующих правых частей с помощью средства типа SolverTable.

МЕНЕДЖЕР. Хорошо, давайте посмотрим, что у нас получилось. Известно, что можно сни­зить стоимость 1 тонны смеси до S500, если снизить требование к содержанию элемента А до 4,75 фунтов в тонне рудной смеси или требование к содержанию элемента С до 27,5 фунтов в тонне. Что делать дальше?

РАЗРАБОТЧИК. Отчет по устойчивости не может здесь помочь. Теперь следует решить, какое изменение более пагубно отразится на свойствах полученной смеси, а это уже чисто технологический вопрос.

МЕНЕДЖЕР. Понятно. Кстати, я думал, что столбец Допустимое увеличение позволяет увеличивать значение правой части. Не могли бы вы показать, что происходит при увеличении правой части?

РАЗРАБОТЧИК. Рассмотрим требование к содержанию элемента А. Предположим, что вы хоти­те повысить данное требование.

МЕНЕДЖЕР. Поскольку мы имеем дело с ограничением вида >=, повышение подразумевает увеличение правой части, т.е. требуемого содержания элемента А.

РАЗРАБОТЧИК. Правильно. Усиление ограничения никогда не приводит к улучшению оптимального зна­чения целевой функции, а может только ухудшить его. В данном случае теневая цена +44,44 показывает, что увеличение правой части данного ограничения приведет к уве­личению оптимальной стоимости тонны смеси. Допустимое увеличение 2,375 означа­ет, что при увеличении исходного показателя 5 на любое количество вплоть до 2,375 прирост стоимости составит 44,44, умноженное на данное количество.

МЕНЕДЖЕР. Иными словами, одна и та же теневая цена действует как при увеличении, так и при уменьшении правой части ограничения. Таким образом, данная теневая цена — это коэффициент изменения значения целевой функции при измене­нии правой части в пределах всего допустимого диапазона.

РАЗРАБОТЧИК. Да, и ослабление ограничения не только не приводит к ухудшению оптимального зна­чения целевой функции, но и может его улучшить. А усиление ограничения, не приво­дя к улучшению оптимального значения целевой функции, может его ухудшить.

МЕНЕДЖЕР. Мы уже говорили, что теневая цена элемента В равна нулю, это означает, что любые отклонения В от значения 100 в пределах указанного диапазона никак не повлияют на оптимальное значение целевой функции. Раз ограничение по В никак не влияет на решение, нельзя ли от него отказаться?

РАЗРАБОТЧИК. Я думаю, что нет. Если когда-нибудь вы захотите изменить некоторые данные и повторно найти решение задачи, ограничение по элементу В может стать лимити­рующим. Например, значение допустимого прироста в данном случае составляет 31,67, а это значит, что если правая часть ограничения превысит 131,67, данное ог­раничение станет лимитирующим. Таким образом, удалять его из модели нельзя.

МЕНЕДЖЕР. Нельзя ли объяснить более понятно?

РАЗРАБОТЧИК. Хорошо. Предположим, что стоимость руды из месторождения 2 может возрасти.

МЕНЕДЖЕР. Должен признаться, я думал о подобной возможности. Но как можно учесть такую неопределенность?

РАЗРАБОТЧИК. Это связано с предыдущим вопросом. Стоимость руды из месторождения 2 — это коэффициент при Т, в целевой функции; в настоящий момент он имеет значение 400. Если эта стоимость возрастает, следует ожидать, что оптимальная ми­нимальная стоимость также будет возрастать. Если стоимость руды из место­рождения 2 возрастет значительно, может получиться, что в оптимальной сме­си этой руды станет меньше или даже не окажется вовсе. Это означает, что бу­дет использоваться больше других руд. Следовательно, относительная важность ограничений может измениться. Ограничения, которые ранее бичи лимитирую­щими, могут перестать быть таковыми, и наоборот. Много всего может про­изойти, когда вы начнете варьировать параметры модели.

МЕНЕДЖЕР. Прекрасно. Однако я так и не понял, какое отношение это имеет к стоимости руды из месторождения 2?

РАЗРАБОТЧИК. Рассмотрим стоимость руды из месторождения 2. На самом деле мы хотим оп­ределить, в каком диапазоне она может изменяться, чтобы это не отразилось на составе оптимальной смеси. Обратимся к таблице Изменяемые ячейки отчета по устойчивости, в которой есть столбцы Допустимое увеличение и Допус­тимое уменьшение. Значения в этих столбцах, соответствующих переменной Т₂, задают диапазон, в котором можно варьировать стоимость Т- так, чтобы это не привело к изменению состава оптимальной смеси.

МЕНЕДЖЕР. Иными словами, в настоящий момент стоимость Т₂ в нашей модели составляет S400, и отчет по устойчивости свидетельствует, что для значений стоимости Т2 в пределах от $100 до $466,85 оптимальные решения останутся прежними. Та­ким образом, если цена возрастет с S400 до $450, нам не о чем беспокоиться.

РАЗРАБОТЧИК. Не совсем так. Мы знаем, что оптимальный состав смеси останется прежним. Это означает, что прежними останутся оптимальные значения всех переменных. Однако общая стоимость возрастет на величину, равную произведению $50 и зна­чения Т2 в данном решении.

МЕНЕДЖЕР. Значит, оптимальное значение целевой функции изменится с $511,11 до 511,11 + 50x0,704 = $546,31, т.е. в данном диапазоне все останется неизменным, кро­ме общей стоимости. Интересно, а что произойдет, если стоимость Т2 увели­чится назначение, которое превысит допустимое?

РАЗРАБОТЧИК. Как известно, в модели минимизации увеличение стоимости компонента не мо­жет привести к увеличению его использования. Поэтому при возрастании стои­мости Т₂ оптимальное значение Т₂ увеличиться не может.

МЕНЕДЖЕР. Таким образом, если удельная стоимость руды из шахты 2 вырастет более чем на допустимое количество, мы получим оптимальное решение, в котором зна­чение Т, будет меньше или равно исходному.

РАЗРАБОТЧИК. Да, и не только это. Оптимальные значения некоторых других переменных также могут измениться, но нельзя сказать, каких именно и на сколько. Это означает, что превышение, которое было положительным, может стать равным нулю, и, следовательно, нелимитирующее ограничение может стать лимитирующим, и наоборот.

МЕНЕДЖЕР. Вы говорите об изменениях стоимости, превышающих допустимое значение. А что будет, если изменение в точности равно предельно допустимому?

РАЗРАБОТЧИК. Тогда появятся альтернативные оптимальные решения: текущее решение и новые решения с меньшим значением Т_г

МЕНЕДЖЕР. По-моему, это очень важная информация. Я даже удивлен тем, как много можно узнать о модели.

РАЗРАБОТЧИК. Это происходит благодаря простоте вычисления данных по устойчивости реше-ния для линейных моделей. Разрешите в качестве проверки задать один вопрос. Как вы уже заметили, оптимальное значение Т₄ равно нулю, предположим, что стоимость Т4 периодически может пересматриваться. На сколько должна сни­зиться цена T4_t чтобы вы захотели приобрести эту руду? МЕНЕДЖЕР. Давайте посмотрим. Текущее значение стоимости Т4 составляет S500 за тонну. Я думаю, что вопрос должен звучать так: на сколько необходимо снизить данную стоимость, чтобы получить оптимальное решение, в которое войдет переменная Т₄? Чтобы ответить на данный вопрос, обратимся к отчету по устойчивости, из которого видно, что если стоимость Т4 снизится менее, чем на $91,11, оптималь-ное значение данной переменной останется неизменным, т.е. нулевым. Из этого можно сделать вывод, что если снизить стоимость до значения меньше 408.89, у модели будет новое оптимальное решение, в котором значение Т₄ положитель­но. Однако что будет, если стоимость снизится ровно на $91.11? Вы сказали, что в этом случае значение Т, станет положительным. Так ли это?

РАЗРАБОТЧИК. Не совсем. В этом случае будет два оптимальных решения: текущее и новое, со­держащее положительное значение Т₄ и новые значения других переменных реше­ния. Но какими станут значения других переменных, мне неизвестно. МЕНЕДЖЕР. Не означает ли это, что при уменьшении стоимости Т4 на $91.ll общая стои­мость внезапно снизится и станет меньше $511,11?

РАЗРАБОТЧИК. Нет, поскольку оптимальное значение целевой функции будет равно $511,11 для каждого решения. МЕНЕДЖЕР. Можно ли узнать, каково значение Т₄ для альтернативной смеси?

РАЗРАБОТЧИК. Можно, но не из отчета по устойчивости. Все, что известно, — данная перемен­ная будет иметь некое положительное значение. Чтобы узнать ее точное значе­ние нужно повторно решить задачу для значения стоимости Т₄, уменьшенного на величину, едва превышающую $91,11. МЕНЕДЖЕР. И последний вопрос. Что означает в отчете по устойчивости столбец с назва­нием Нормированная стоимость?

РАЗРАБОТЧИК. Смысл имеют только ненулевые элементы нормированной стоимости. Для пере­менной решения, оптимальное значение которой равно нулю, существуют две эк­вивалентные интерпретации ее нормированной стоимости. В модели минимиза­ции, такой как наша, нормированная стоимость, во-первых, показывает, на сколько следует уменьшить удельную стоимость данной переменной решения, чтобы оптимальное значение этой переменной стало ненулевым. Во-вторых, это теневая цена ограничения неотрицательности для данной переменной решения. Вспомним, что если переменная решения равна нулю, то ограничение неотрица­тельности для данной переменной является лимитирующим, тогда, согласно оп­ределению теневой цены, нормированная стоимость представляет собой коэффи­циент ухудшения оптимального значения целевой функции в случае, если мы от­вергнем решение, предложенное средством Поиск решения, и заставим данную переменную принимать положительные значения, увеличив правую часть ограни­чения неотрицательности.

Первую интерпретацию нормированной стоимости иногда называют интерпре-тацией вознаграждения — на сколько должна улучшиться данная удельная стои­мость, чтобы Поиск решения увеличил соответствующую переменную решения до положительного значения с целью понизить общую стоимость. Вторую интер­претацию нормированной стоимости иногда называют интерпретацией штра­фа — на сколько испортится решение, если заставить Поиск решения увеличить данную переменную решения до положительного значения.

МЕНЕДЖЕР. Первая интерпретация относится к изменениям коэффициентов целевой функции, а мы только что рассмотрели аналогичный вопрос для переменной Т₄. В отчете по устойчивости я вижу одно и то же значение 91,11 в столбце Допустимое уменьше­ние и Нормированная стоимость. Зачем нужен столбец Нормированная стои­мость, если то же самое значение содержится в столбце Допустимое уменьшение? РАЗРАБОТЧИК. Действительно, первая интерпретация нормированной стоимости связывает ее с из­менениями коэффициентов целевой функции, поэтому одинаковые числа всегда содер­жатся в столбце нормированной стоимости и в первом или втором столбце допусти-мьсс изменений. Однако размещение данных о нормированной стоимости в том же столбце отчета по устойчивости, в котором находятся теневые цены, напоминает о второй интерпретации, которая рассматривает нормированную стоимость в каче­стве теневой цены. Вы можете выбрать ту интерпретацию, которая вам удобней. МЕНЕДЖЕР. Спасибо, наша беседа была весьма плодотворной.

4.11. Характеристика отчета по устойчивости

После оптимизации модели линейного программирования таблица модели и отчет по устойчивости средства Поиск решения содержат следующую информацию.

1. Оптимальные значения переменных решения, значения резерва и излишка (раз­ности между значениями левых и правых частей ограничений), а также значение целевой функции. Ограничения с нулевым резервом или излишком называются лимитирующими, они препятствуют дальнейшему улучшению целевой функции. Ограничения с положительным значением резерва или излишка называются нели-митирующими.

2. Теневая цена в отчете по устойчивости отражает коэффициент изменения опти­мального значения целевой функции при увеличении правой части ограничения. Допустимые увеличение и уменьшение задают допустимый диапазон изменений правой части, в котором теневая цена сохраняет свое значение.

3. Допустимые увеличение и уменьшение для коэффициентов целевой функции пока­зывают, какие изменения можно вносить в коэффициенты целевой функции, чтобы это не привело к изменению оптимального решения. Если значение изменения ко­эффициента целевой функции равно допустимому, это приведет к появлению аль­тернативного оптимального решения с новыми значениями переменных (при усло­вии невырожденности). Если изменение коэффициента превышает допустимое, оп­тимальное решение изменится (также при условии невырожденности).

4. Строго говоря, нормированная стоимость имеет смысл только для тех переменных решения, оптимальное значение которых равно 0. В таком случае данный элемент можно интерпретировать как теневую цену ограничения неотрицательности для данной переменной (если такое ограничение существует); он содержит ту же ин­формацию, что и допустимое увеличение или уменьшение для данной перемен­ной. Если значения как нормированной стоимости, так и переменной решения ненулевые, это значит, что существует ограничение для данной переменной, кото­рое является лимитирующим, и нормированная стоимость— теневая цена дан­ного лимитирующего ограничения, а не ограничения неотрицательности."

Различные интерпретации нормированной стоимости также рассматриваются в разделе 4.12.

лами не может добиться более 9,33%. "Это потому, что они не разбираются в оптимиза­ции, маргинальном анализе и роли теневых цен!" — ответил Уэйн. Начальник не стал ос­тужать энтузиазм нового управляющего и спросил, сможет ли Уэйн получить 12% при­были с дополнительных $5 000 000. Быстро проверив значение допустимого увеличения для бюджетного ограничения, Уэйн попросил босса прислать его филиалу все S5 000 000 и даже больше.

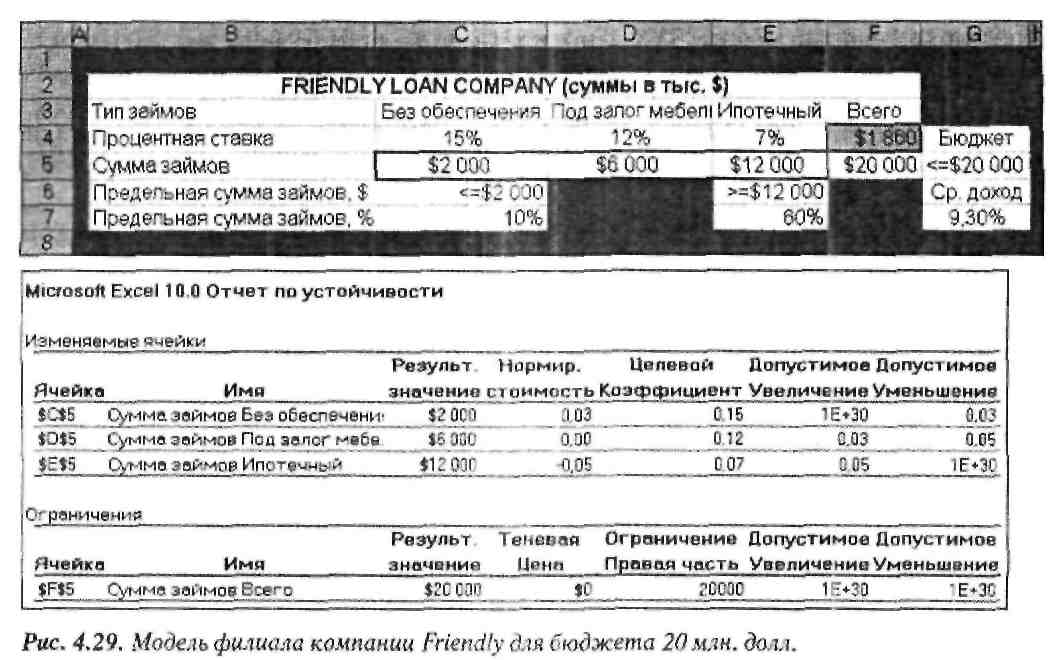
Однако, повесив трубку, Уэйн ощутил некие сомнения: "В модели помимо ограниче­ний неотрицательности было три ограничения. Что же случилось в отчете по устойчиво­сти с лимитирующими ограничениями для двух типов ссуд? Вместо одного там должно быть три ограничения вместе с соответствующими теневыми ценами". Поскольку его беспокойство росло, он решил проверить информацию отчета по устойчивости, введя новое значение бюджета 20 000 в ячейку G5. Запустив Поиск решения для нового значе­ния правой части ограничения, он получил результаты, показанные на рис. 4.29. Уэйн был шокирован, когда увидел, что средняя прибыль в ячейке G7 для новой модели оста­лась неизменной и составила 9,3%. Поскольку удельная прибыль для дополнительных $5 млн. составляет 12%, он ожидал, что средняя прибыль его портфеля также возрастет.

Больше не доверяя ни средству Поиск решения, ни Excel, Уэйн схватил свой кальку­лятор и, разделив разность двух значений суммарного процентного дохода, полученных с помощью Поиск решения, на прирост бюджета ((1860— 1395)/5ОО0) увидел, что удельная прибыль для дополнительных $5 млн. в действительности составляет 9,3%, а не 12%. Он скептически посмотрел на теневую цену бюджетного ограничения и допусти­мый диапазон в новом отчете по устойчивости на рис. 4.29 и пришел к выводу, что про­грамма дважды обманула его. В смущении Уэйн подошел к телефону, чтобы сообщить начальнику о своей ошибке.

Что же произошло? Может быть, данные были неверно масштабированы, что привело к неправильным отчетам средства Поиск решения? Или же Поиск решения действитель­но дает неверные результаты для некоторых моделей? Если это не так, как объяснить значение 0,120 теневой цены бюджетного ограничения на рис. 4.28 и 4.29? И что случи­лось с информацией о теневой цене для двух других ограничений, которая почему-то от­сутствует в обоих отчетах по устойчивости?

Хотя подобное подозрение заслуживает внимания, в данном случае диапазон значе­ний параметров модели недостаточно велик, чтобы привести к ошибкам в работе средст­ва Поиск решения, что могут подтвердить результаты повторной оптимизации (нужно установить опцию Автоматическое масштабирование в диалоговом окне Параметры поиска решения и повторно выполнить оптимизацию). Чтобы разобраться, что про­изошло на самом деле, переформируем модель, используя рекомендованные в главе 3 правила представления. В результате получим оптимальное решение и отчет по устойчи­вости (рис. 4.30).

Как показано на рис. 4.27 и 4.30, обе формулировки задачи ЛП приводят к одним и тем же оптимальным решениям по ссудам и одинаковому значению суммарного про­центного дохода. Различия возникли в отчетах по устойчивости и их интерпретации. Рас­смотрим результаты работы модели ЛП. построенной согласно изложенным в главе 3 правилам. Во-первых, на рис. 4.30 в отчете по устойчивости присутствуют все три огра­ничения, а также связанные с ними теневые цены и допустимые диапазоны изменений правых частей. Во-вторых, теневая цена бюджетного ограничения на рис. 4.30 имеет пра­вильное значение 9,3%. В-третьих, те из вас, кто ознакомился уже с вопросами вырожде­ния моделей ЛП, изложенными в разделе 4.13, могут заметить, что решения обеих задач являются невырожденными (в чем легко убедиться, подсчитав на рис. 4.30 общее количе­ство ненулевых переменных решения (равно 3) и сравнив его с числом ограничений (также равно 3)). В-четвертых, в отличие от отчета по устойчивости первой модели Уэй-на, в столбце Нормированная стоимость на рис. 4.30 правильно указаны нулевые значе­ния для всех трех переменных решения, поскольку ни одна из них не равна нулю, т.е. ни одно из ограничений неотрицательности не является лимитирующим.

Из этого следует, что отчет по устойчивости для исходной модели Уэйна на рис. 4.28 (с пропущенными теневыми ценами и диапазонами, неправильными данными о нормированной стоимости и неверной теневой ценой бюджетного ограничения) со­вершенно неудовлетворителен, а для стандартной формулировки задачи ЛП на рис 4.30 составлен вполне нормальный отчет. С другой стороны, табличное представление Уэйна на рис. 4.27 значительно легче понимать и интерпретировать, чем рекомендуемую фор­мулировку задачи на рис. 4.30. Похоже, у нас нет выбора: удобное и компактное лред-ставление приводит к неверным результатам в отчете по устойчивости, а корректную ин­формацию о чувствительности решения можно получить только с помощью громоздкой модели. Однако это не так: обе модели совершенно корректны, и ошибок в отчетах по ус­тойчивости нет. Таким образом, можно воспользоваться преимуществами более удоб­ного представления и в то же время не получить ошибок в отчете по устойчивости. Но

для этого требуется более глубокое понимание работы средства Поиск решения, чем есть у Уэйна. Итак, чтобы разрешить данный "парадокс", рассмотрим более детально, как ра­ботает средство Поиск решения.

Простые ограничения

Сколько времени и машинной памяти потребуется средству Поиск решения для оп­тимизации модели, определяется, главным образом, размерами матрицы коэффициен­тов. составляющих левые части ограничений (например, содержащихся в ячейках C7:F9 на рис. 4.30). Размерность матрицы коэффициентов ограничений вычисляется как про­изведение числа переменных решения (столбцов) и числа ограничений (строк). Умень­шив любое изданных чисел, можно уменьшить размер матрицы и, следовательно, сокра­тить время оптимизации. Поиск решения включает в себя процедуру, которая позволяет обрабатывать любые простые ограничения, где участвует только одна переменная реше­ния (кроме ограничений неотрицательности), не рассматривая их как ограничения. Это позволяет сделать матрицу коэффициентов меньше, сократить время оптимизации и по­требность в оперативной памяти компьютера, или, что то же самое, позволяет на том же компьютере оптимизировать модели ЛП большей размерности. Платой за использование этой возможности обработки простых ограничений является потеря некоторой инфор­мации в отчете по устойчивости. Единственной информацией для всех простых ограни­чений в этом отчете будут их теневые цены, которые не сопровождаются данными о диа­пазонах их применимости.

Поскольку, как правило, только одно простое ограничение может быть лимитирую­щим для определенной переменной решения в точке оптимальности, а информация о диапазоне отсутствует, для компактности отчета по устойчивости соответствующая не­нулевая теневая цена простого ограничения (если таковая имеется) указывается после своей переменной решения. Столбец Нормированная стоимость отчета по устойчивости всегда содержит по одной ячейке для каждой переменной решения, поэтому Поиск ре­шения помещает ненулевую теневую цену простого ограничения в столбец Нормирован­ная стоимость после соответствующей переменной решения. Например, теневые цены двух ограничений для типов ссуд указаны на рис. 4.30 в стандартном виде и составляют 3% для ограничения на ссуды без обеспечения и —5% для ограничения ипотечных ссуд. Те же самые значения представлены на рис. 4.28 в отчете для модели Уэйна в столбце Нормированная стоимость сразу после соответствующих переменных решения. По­скольку для каждой из двух переменных решения в модели ЛП задано по два ограниче­ния, сразу непонятно, какие из них являются лимитирующими, и каким из них соответ­ствуют ненулевые значения в столбце Нормированная стоимость отчета по устойчиво­сти для модели Уэйна.

Для ссуд без обеспечения задано простое ограничение неотрицательности и простое ограничение вида <$1500. Однако эти ограничения не могут быть лимитирующими од­новременно. В данном случае лимитирующим является второе ограничение; таким обра­зом, число 0,03 в столбце Нормированная стоимость отчета для модели Уэйна должно быть теневой ценой ограничения "Сумма ссуд без обеспечения < $1500". Поскольку ог­раничение "Сумма ссуд без обеспечения >0" не является лимитирующим, его теневая цена должна быть нулевой.

Для переменной решения, определяющей сумму ипотечных ссуд, также задано два ограничения: "Сумма ипотечных ссуд > 0" и "Сумма ипотечных ссуд > 9000", причем они не могут быть лимитирующими одновременно. Поскольку значение данной переменной

решения составляет $9000, теневая цена в столбце Нормированная стоимость отчета для модели Уэйна соответствует лимитирующему простому ограничению "Сумма ипотечных ссуд > 9000". Поскольку второе ограничение ("Сумма ипотечных ссуд >0") лимитирую­щим не является, его теневая цена равна нулю.

Таким образом, информация о теневой цене не теряется при использовании простых ограничений в моделях ЛП, мы выяснили, где ее искать и как определить, какому огра­ничению соответствует конкретное ненулевое значение теневой цены. Поскольку зада­ние простых ограничений на переменные решения приводит к более удобному представ­лению таблицы и позволяет быстрее находить решение задачи (что немаловажно для мо­делей больших размеров), их достаточно активно используют при формировании табличных моделей ЛП. Однако следует помнить, что использование простых ограниче­ний приводит к тому, что в отчете по устойчивости нарушается стандартная интерпрета­ция нормированной стоимости, данная в разделе 4.10.

Напомним, что в одной из интерпретаций нормированная стоимость переменной ре­шения рассматривается как теневая цена ограничения неотрицательности для данной переменной. В моделях ЛП, содержащих простые ограничения, числа в столбце Норми­рованная стоимость соответствуют теневым ценам тех ограничений, которые являются лимитирующими для указанных переменных решения. В приведенной ниже таблице представлена более сложная картина того, какими могут быть значения нормированной стоимости в моделях ЛП, содержащих простые ограничения.

Есть ли возможность получить из отчета по устойчивости информацию о допустимых диапазонах правых частей простых ограничений? К сожалению, нет. Если возможно, Поиск решения всегда представляет отчет по устойчивости в такой форме, как на рис. 4.30. Если информация о диапазонах правых частей простых ограничений важна, необходимо перестроить табличное представление модели ЛП так, чтобы средство Поиск решения не смогло обнаружить наличие в модели простых ограничений и повторно оп­тимизировать полученную модель. Поиск решения не вызывает свою процедуру обра­ботки простых ограничений, если они заданы в таблице неявно. Для этого можно ис­пользовать некоторую промежуточную формулу, как, например, на рис. 4.30 формулы в ячейках G7:G9, каждая из которых связывает переменную решения с ее правой частью неравенства посредством значений трех ячеек, содержащих коэффициенты левых частей ограничений. Если же Excel обнаружит в диалоговом окне Поиск решения адрес любой из изменяемых ячеек в поле Ограничения (за исключением ограничений неотрицатель­ности), будет вызвана специальная процедура обработки простых ограничений. Натри-мер, в модели Уэйна на рис. 4.27 адреса изменяемых ячеек С5 и Е5 для первых двух огра­ничений перечислены в поле Ограничения диалогового окна Поиск решения, что при­водит к вызову процедуры обработки простых ограничений.

Интерпретация теневой цены

Как уже отмечалось, значение теневой цены бюджетного ограничения в модели Уэйна, равное 0,120, оказалось неверным; более того, именно его интерпретация теневой цены стала причиной всех неприятностей Уэйна. Заметим, что модель на рис. 4.27 содержит формулы в правой части ограничений, задающих предельные значения для ссуд без обеспе­чения и ипотечных ссуд, что является нарушением одной из рекомендаций по созданию табличного представления (см. главу 3). Напомним определение теневой цены: это измене­ние оптимального значения целевой функции при изменении правой части заданного огра­ничения на единицу, когда все другие параметры, включая правые части других ограниче­ний, остаются постоянными. Следовательно, теневую цену 0,120, содержащуюся в отчете по устойчивости на рис. 4.28, следует интерпретировать так: если зафиксировать правые части ограничений, задающих предельные значения для ссуд без обеспечения и ипотечных ссуд, на исходном уровне $1500 и $9000 соответственно, то улучшение значения целевой функции составит 0,12 для каждого дополнительного бюджетного доллара.

Если оставить суммы ссуд без обеспечения и ипотечных ссуд на исходном уровне, до­полнительный бюджетный доллар в модели Уэйна может пойти только на ссуду под залог мебели, процентная ставка для которой составляет 12%. Таким образом, программа По­иск решения совершенно правильно указала теневую цену для модели Уэйна. Очевидно, что фиксация правых частей для ссуд без обеспечения и ипотечных ссуд на исходном долларовом уровне не согласуется с результатами повторного решения, в котором изме­няются все правые части, чтобы отразить новые предельные значения, обусловленные появлением дополнительного бюджетного доллара. Уэйн ошибочно предположил, что ограничения на объемы ссуд будут соблюдаться в отчете по устойчивости для его модели, но этого не произошло из-за наличия формул в правых частях двух ограничений.

В формулировке задачи ЛП на рис. 4.30 ошибочной интерпретации удалось избежать, поместив все формулы в левые части ограничений и оставив в правых частях одни кон­станты. Когда все формулы связи с бюджетом находятся в левых частях ограничений, Поиск решения вносит необходимые изменения во все левые части при оценке удель­ного вклада дополнительного бюджетного доллара. В результате этого согласования ле­вых частей формируется отчет по устойчивости (см. рис. 4.30), в котором указано верное значение теневой цены 0,093. Модель на рис. 4.30 отражает все ограничения компании Friendly, которые Уэйн пытался представить в своей модели.

Из данного примера можно сделать следующий вывод: использование простых огра­ничений, а также формул в правых частях ограничений в формулировке задач ЛП позво­ляет сделать их табличные представления более компактными и понятными. Поэтому мы будем широко использовать такие представления моделей ЛП в последующих трех гла­вах. Однако следует помнить, что в таком случае потребуются дополнительные усилия для извлечения необходимой для принятия решений информации из отчета по устойчи­вости, сгенерированного средством Поиск решения.