4.9. Анализ чувствительности с помощью надстройки SolverTable

К недостаткам отчета по устойчивости, генерируемым средством Поиск решения, от­носится то, что, во-первых, он предоставляет информацию по устойчивости решения лишь в непосредственной близости от полученного оптимального решения, причем в от­вет на изменения только одного параметра. Во-вторых, предоставляемая информация касается только воздействия на оптимальное значение целевой функции, и. в-третьих, в нем нет данных по устойчивости решения при изменении технологических коэффици­ентов модели (т.е. коэффициентов в левых частях ограничений). Чтобы выяснить, каким будет решение при значительных изменениях параметров, при одновременном измене­нии нескольких параметров либо при изменении технологических коэффициентов, не­обходимо вручную вносить новые данные, повторно находить решение задачи и вручную фиксировать полученные результаты. В главе 2 при анализе чувствительности мы ис­пользовали таблицы подстановки Excel, чтобы зафиксировать сразу несколько сценариев "Что-если". К сожалению, таблицы подстановки нельзя использовать для фиксирования результатов оптимизации модели ЛП, поскольку в процессе создания таблиц подстанов­ки Excel просто пересчитывает рабочий лист, но не может самостоятельно вызвать сред­ство Поиск решения.

На прилагаемом к данной книге компакт-диске имеется надстройка SolverTable.xla. Это средство содержит макрос, создающий таблицы, подобные таблицам подстановки, для вновь оптимизированной модели ЛП после каждого изменения ее параметров. Кроме того, SolverTable знает про отчет по устойчивости и может также фиксировать содержащуюся в нем информацию. Наконец, возможности SolverTable не ограничивается моделями с дву­мя переменными (в отличие от GLP), она может работать с оптимизационными моделями любой размерности, допустимой для встроенной в Excel надстройки Поиск решения или программы Premium Edition Solver for Education. В данной главе мы проиллюстрируем ис­пользование надстройки SolverTable на примере упрощенной модели Oak Products.

Для начала откройте с прилагаемого к книге компакт-диска рабочую книгу OakProd.xls. Затем с помощью команды Файл ->Открыть откройте файл надстройки SolverTable.xla. Excel откроет диалоговое окно с предупреждением, показанное на рис. 4.18, в этом окне щелкните на кнопке Не отключать макросы. После этого в меню Сервис появится новая команда SolverTable. Однако, как и при создании таблиц подстановки, сначала необходимо сформировать таблицу результатов.

Изменение правых частей ограничений

Чтобы проиллюстрировать работу с SolverTable, проведем анализ чувствительности решения к изменениям правой части ограничения по длинным штифтам. Подобный анализ мы проводили в главе 3 с помощью таблицы подстановки с одним входом На­помним, что таблица подстановки с одним входом позволяет менять только один пара­метр, при этом можно фиксировать любое количество выходов модели. Сначала размес­тим диапазон значений правой части ограничения в одном столбце (или строке) — на рис. 4.19 значения правой части от 399 до 1350 внесены в ячейки 17:117. Затем, как к при создании таблицы подстановки с одним входом, в верхнюю часть таблицы в ячейки .16:Р6 введем ссылки на ячейки, содержащие выходы модели (формулы в этих ячейках показа­ны на рис. 419 в виде выносок). Формулы в ячейках J6:M6 ссылаются на значение левой части ограничения подлинным штифтам, на два значения переменных решения и значе­ния прибыли (целевой функции) соответственно. Формулы в ячейках N6:P6 указывают на ячейки отчета по устойчивости средства Поиск решения, содержащие теневую цену, допустимое увеличение и допустимое уменьшение для данного ограничения (ячейки, на которые указывают ссылки, можно увидеть на рис. 4.11). Заголовки в ячейках I5:PS яв­ляются необязательными и служат для удобства документирования.

Замечание. При использовании SolverTable требуется, чтобы модель ЛП была предвари­тельно оптимизирована с помощью Поиск решения. Если в создаваемой таблице предпо­лагается фиксировать какие-либо элементы отчета по устойчивости, необходимо, чтобы этот отчет был сгенерирован средством Поиск решения.

Затем созданную таблицу следует выделить и выбрать команду SolverTable из меню Сервис. Как и при создании таблиц подстановки, SolverTable предлагает диалоговое ок­но с двумя полями ввода, в которых указывается, где на рабочем листе расположены ячейки, куда подставляются введенные значения. Поскольку в данном случае изменяется только один параметр — правая часть ограничения длинных штифтов, и в созданной таб­лице его значения помещены в столбец, адрес ячейки F6 вводится в поле Input Соlumn Cell⁷, а другое поле в диалоговом окне SolverTable остается пустым. После этого SolverTable будет запускать Поиск решения для каждого из указанных значений правой части ограничения. В данном случае будет выполнено 11 оптимизаций, и для каждой из них зафиксируются перечисленные в таблице результаты модели (рис. 4.20).

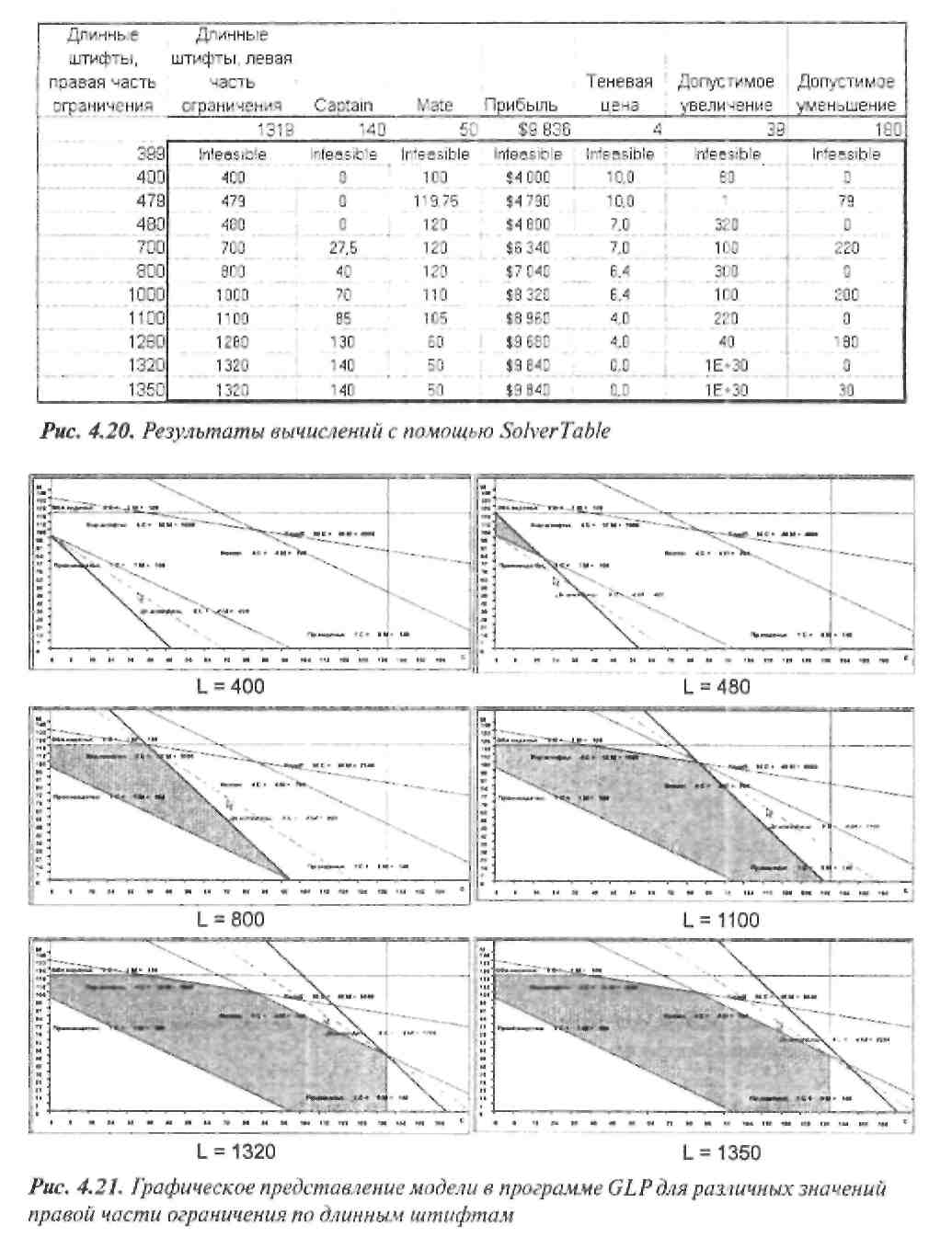
На рис. 4.21 изображены различные представления модели Oak Products в программе GLP для различных значений исходного запаса длинных штифтов L, содержащихся в таблице на рис. 4.20. Здесь видно, что увеличение значений L с 400 до 1350 приводит к расширению допустимой области до тех пор, пока ограничение по длинным штифтам не становится избыточным. Более того, сравнение числовых результатов на рис. 4.20 и графических представлений модели на рис. 4.21 показывает, что теневая цена резко ме­няется всякий раз, когда меняется комбинация ограничений, определяющих оптималь­ное угловое решение. Также нетрудно заметить, что, поскольку значения теневой цены уменьшаются (скачкообразно) по мере увеличения L, коэффициент возрастания опти­мального значения целевой функции снижается; это явление достаточно типично для моделей максимизации при ослаблении одного ограничения вида <.

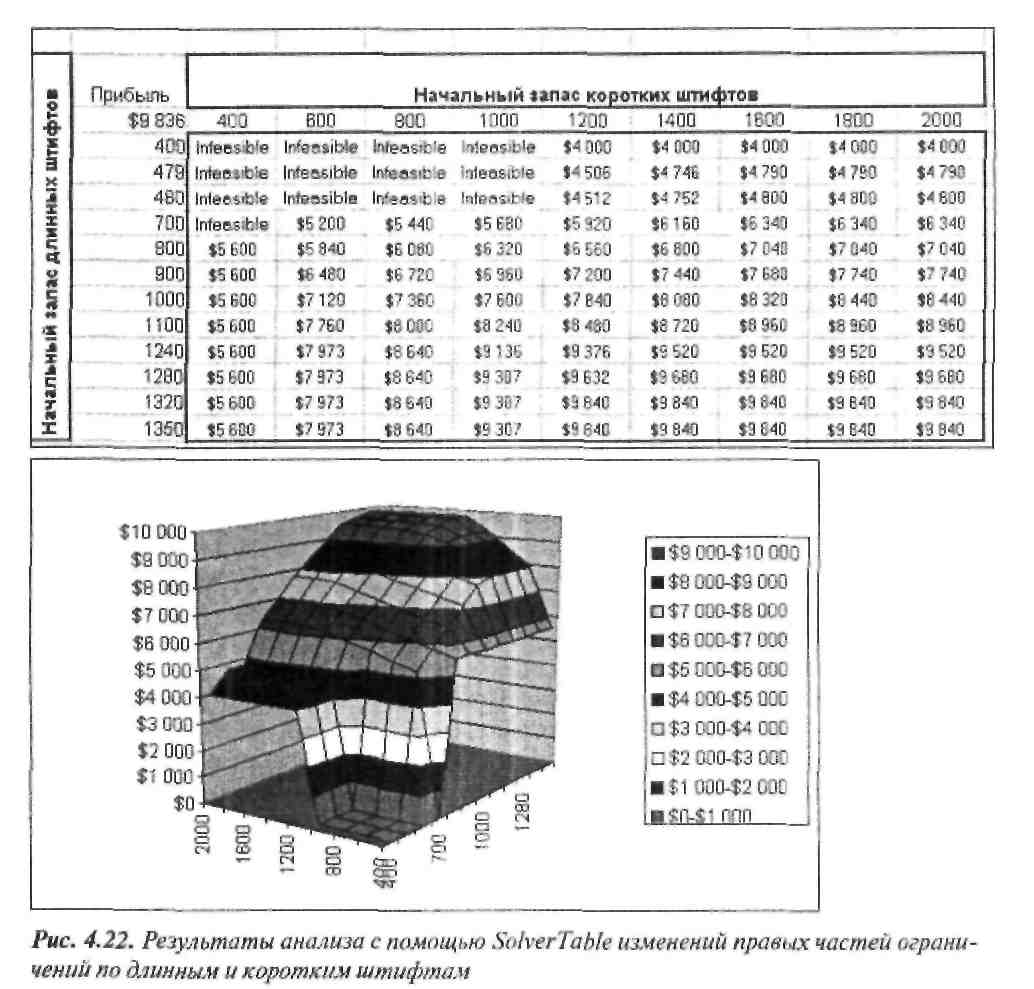
В отчете по устойчивости одновременно изменяется только один параметр, остальные данные при этом остаются фиксированными. SolverTable, как и таблица подстановки с двумя входами, позволяет варьировать одновременно два параметра, однако при этом можно фиксировать значения только одной итоговой ячейки. В качестве иллюстрации рассмотрим различные диапазоны значений правых частей ограничений для длинных и коротких штифтов. Как и ранее, сначала создается таблица, в данном случае в ней ука­заны значения обоих параметров. После этого SolverTable запускает Поиск решения для каждой пары значений правых частей ограничений по длинным и коротким штифтам; в данном случае придется выполнить 108 оптимизаций, для каждой из которых в таблицу заносится значение единственного результирующего показателя — значения целевой функции (ссылка на соответствующую ячейку содержится в левом верхнем углу табли­цы), как показано на рис. 4.22. Неудивительно, что оптимальное значение целевой функ­ции возрастает при увеличении одного или обоих значений правых частей. Далее с по­мощью мастера диаграмм можно легко построить график зависимости оптимального значения целевой функции от значений правых частей ограничения. Такой график на рис. 4.22 показывает снижение прироста оптимального значения целевой функции, по мере ослабления ограничений.

При созданиии таблиц подстановки в диалоговом окне Таблица аналогичное поле называется Подстав­лять значения по строкам. — Прим. ред.

Изменение коэффициентов целевой функции

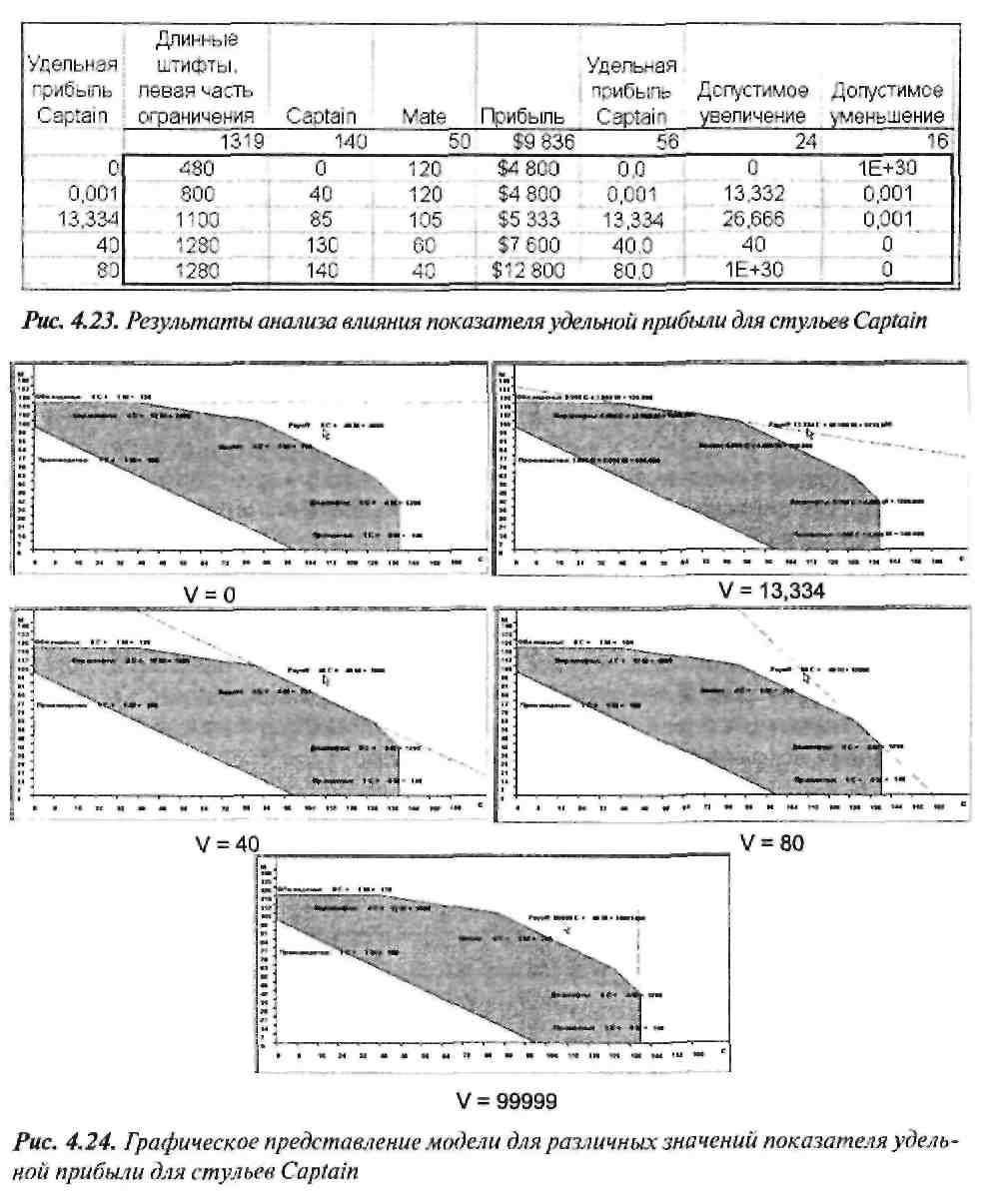
Исследование влияния коэффициентов целевой функции с помощью SolverTable ана­логично исследованию влияния правой части ограничений. Сначала создается таблица, в столбец (или строку) которой заносятся значения исследуемого коэффициента целевой функции. На рис. 4.23 представлены результаты анализа влияния коэффициента целевой функции, отражающего удельную прибыль для стульев Captain. При этих значениях ко­эффициента решение задачи меняется, о чем говорят значения в столбце Допустимое увеличение. На рис. 4.24 показаны представления модели Oak Products в программе GLP при различных значениях коэффициента V целевой функции для стульев Captain, задан­ных в таблице на рис. 4.23. При возрастании значений V от 0 до 99999 прямая целевой функции поворачивается, становясь из горизонтальной практически вертикальной. Бо­лее того, сравнение данных на рис. 4.23 и 4.24 показывает, что оптимальное решение ме­няется скачкообразно в точках критических значений V. Наконец, появление нулей в столбце Допустимое увеличение или Допустимое уменьшение для критических зна­чений V показывает наличие множественных оптимальных решений.

Изменение технологических коэффициентов

С помощью SolverTable можно достаточно просто исследовать альтернативные произ­водственные технологии. Напомним, что функции ограничений и их коэффициенты оп­ределяют вычисление левых частей, а следовательно— спрос на ресурсы, отражая тем самым определенную технологию. Предположим, компания Oak Products рассматривает возможность небольшого повышения или снижения прочности стульев Mate путем уве­личения или уменьшения количества используемых для производства одного стула длинных штифтов. Помимо инженерной оценки данных изменений, руководство ком­пании хочет провести экономический анализ последствий уменьшения количества ис-

пользуемых для сборки одного стула Mate длинных штифтов с 4-х до 2-х и увеличения свыше 4-х. Этот анализ не столь уж очевиден: данное изменение не только непосредст­венно отразится на цене стула, но и повлияет на потребность в длинных штифтах, запас которых ограничен. Это может сказаться на производственных возможностях, что в свою очередь может привести к иным планам выпуска стульев обоих видов. Таким образом, необходима повторная оптимизация модели с помощью SolverTable.

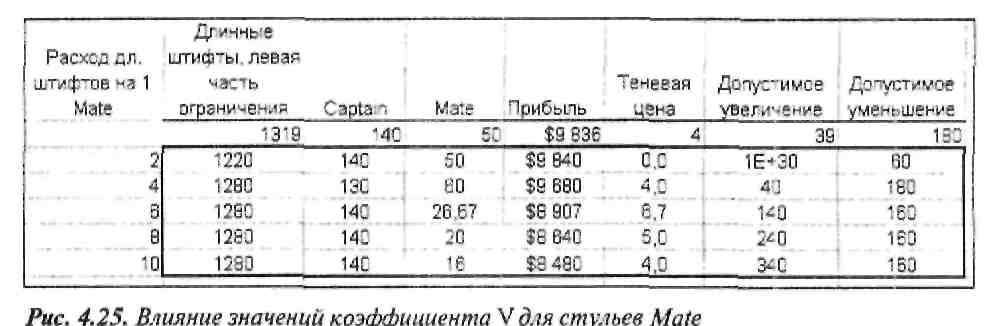
Процедура применения SolverTable в данном случае аналогична описанному выше анализу влияния правой части ограничения: надо сформировать таблицу, задав различ­ные значения технологического коэффициента в окрестности базового значения 4, а за­тем запустить SolverTable, чтобы зафиксировать представляющие интерес итоговые пока­затели модели. В результате получится таблица, содержащая показатели модели при из­менении расхода длинных штифтов на изготовление одного стула Mate в диапазоне 2-10 (рис. 4.25).^s Как и ожидалось, увеличение расхода длинных штифтов на изготовление од­ного стула Mate с 4 до 6 приводит к уменьшению оптимального выпуска этих стульев, ко­торое компенсируется увеличением выпуска стульев Captain, при этом происходит сни­жение суммарной прибыли примерно на $570. Удивительно, но уменьшение расхода длинных штифтов на изготовление одного стула Mate с 4 до 2 также приводит к сниже­нию значения оптимального выпуска этих стульев и увеличению выпуска стульев Captain, однако при этом общая прибыль возрастает. Другие представленные на рис. 4.25 результаты, в частности, теневая цена длинных штифтов, претерпевают аналогичные из­менения. Принимая во внимание, что все связи модели линейны, такие противоречащие интуиции результаты решения задачи ЛП часто являются неожиданностью, поскольку они отражают скрытые и порой непредсказуемые взаимодействия между ограничениями даже простейшей модели линейного программирования.

На этом мы завершаем обсуждение данных, содержащихся в отчете по устойчивости. Овладев изложенным материалом, вы сможете использовать модели линейного програм­мирования на практике — формировать модели, оптимизировать их с помощью средства Поиск решения, правильно интерпретировать отчет по устойчивости, а также использо­вать надстройку SolverTable для более углубленного анализа параметров. Но мы еще не рассмотрели пример анализа чувствительности для модели минимизации и не объяснили значение данных Нормированная стоимость в отчете по устойчивости. Эти вопросы рассматриваются в следующем разделе.

При выполнении расчетов предполагалось, что исследуемый коэффициент целевой функции (удельная при­быль в расчете на один стул Mate) остался неизменным, т.е. влияние изменения расхода длинных штифтов на переменные издержки не учитывалось,