70. Порядок расчета абсорбера

1.При расчете абсорберов обычно заданы: расход газа, его начальная и конечная концентрация(иногда вместо концентрации задается степень извлечения φ), степень разделения, состав смеси на выходе из абсорбера, начальная концентрация абсорбента.

2.Выбор поглотителя, абсорбента

3.Расчеты материального баланса по газовой фазе

4.Выбор режима проведения процесса

5.Расчет условий равновесия

6. Произвести расчет рабочего и минимального расхода абсорбента

7.Установить состав отработанного поглотителя

8.Выбор конструкции абсорбера, контактных устройств

9.Определение рабочей скорости газа через абсорбер

10.Определение D аппарата и поперечного сечения аппарата

11.Расчет высоты рабочей зоны и высоты аппарата

12.Расчет гидравлического сопротивления аппарата

13.Определение высоты сепарационной части аппарата, диаметра штуцеров(абсорбера).

71. закономерности фазового равновесия. Если система состоит из двух компонентов (К = 2) и между ними не происходит химического взаимодействня, то при наличии жидкой и паровой фаз число фаз Ф = 2. Согласно правилу фаз, число степеней свободы такой системы составляет:

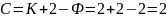
Следовательно, из трех независимых параметров, полностью определяющих состояние системы – температуры t давления р и концентрации одной из фаз с – можно произвольно выбрать любые два; при этом определится значение третьего параметра, которое уже не может быть произвольным. В связи с этим для физико-химической характеристики бинарных систем жидкость – пар удобно пользоваться так называемыми фазовыми диаграммами. Если обозначить через х состав жидкой фазы, а через у состав паровой фазы, то принимая t = соnst, можно построить график зависимости давления пара от состава жидкости (диаграмма р – х). Аналогично, полагая постоянным давление паров изображают на плоскости зависимость температур кипения жидкости и конден­ации паров от составов жидкой и паровой фаз (диаграмма t – х – у). Наконец, при t = соnst и р=const находят зависимость между равновесными составами фаз, которая изображается диаграммой равновесия (у — х). Вид этих зависимостей определяется взаимной растворимостью компонентов жидкой смеси и другими их свойствами, рассматриваемыми ниже. Идеальные смеси: идеальные растворы следуют законам Рауля и Дальтона. Согласно закону Рауля, парциальное давление каждого компонента, например низкокипящего компонента А в паре пропорционально моль­ной доле этого компонента в жидкости При этом коэффициент пропорциоальности равен давлению насыщенного пара данного компонента при данной температуре. При смешивании компонентов идеального раствора тепловой эффект отсутствует и объем смеси практически не изменяется. Для бинарной смеси, состоящей из компонентов А и В, но закону Рауля:

Одновременно, согласно закону Дальтона – давление пара над раствором Р равно сумме парциальных давлений его компонентов.

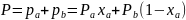
Из уравнений, выражающих законы Рауля и Дальтона, видно, что при постоянной температуре парциальные давления компонентов, а также общее давление паров над смесью находятся в линейной зависимости от мольной доли х_л низкокипящего компонента. Реальные смеси: реальные жидкие смеси с полной взаимной растворимостью компонентов не следуют закону Рауля. Отклонение от этого закона в каждой из фаз может быть положительным или отрицательным, причем последнее наблюдается реже. При положительном отклонении от закона Рауля разность давлений Р – Р_ид> 0, при отрицательном отклонении Р – Р_ид<0, где Р – общее давление над реальным раствором, а Р_ид – над идеальным раствором. Отклонения от закона Рауля связаны с изменением активности молекул в растворе, обусловленным химическим взаимодействие и между ними, диссоциацией и др. Степень отклонения свойств реального раствора от свойств идеального раствора определяется величиной коэффициента активности γ, равного отношению активности компонента раствора к его концентрации. В отличие от идеального раствора, для которого γ_А=γ_В=1 парциальные давления компонентов А и В неидеальной бинарной смеси составляют:

,

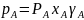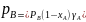
Т ипичные диаграммы р – х, t – х – у и у – х для систем с максимумом температуры кипения показаны на рисунке а, с минимумом температуры кипения – на рисунке б. Как видно из рисунка максимуму общею давления пара соответстиует минимум температуры кипении смеси и наоборот. Точка М, в которой кривые составов фаз пересекают диагональ на диаграмме у – х, называется азеотропной точкой. Она указывает состав смеси, которая при данном давлении не может быть разделена перегонкой на составляющие ее компоненты. Состав азеотропных смесей зависит от температуры (давления). Эта зависимость характеризуется вторым законом Вревского: при повышении температуры азеотропной смеси, обладающей максимумом давления пара, в смеси увеличивается относительное содержание того компонента, парциальная мольная теплота испарения которого больше а для смеси с минимумом пара – содержание компонента, парциальная мольная теплота испарения которого меньше. Этот закон указывает принципиальную возможность разделения азеотропных смесей путем изменения давления при перегонке. С изменением давления азеотропная точка перемещается на равновесной кривой. При совладении этой точки с правым верхним углом квадранта диаграммы у – х в большинстве случаев удается разделить азеотропную смесь перегонкой.

73. Простая перегонка. Фрикционная перегонка. Перегонку проводят путем постепенного испарения жидкости, находящейся в перегонном кубе Образующиеся пары отводятвя и конденсируются. Процесс осуществляют периодическим или непрерывным способом. Если простая перегонка проводится периодически, то в ходе отгонки НК содержание его в кубовой жидкости уменьшится. Вместе с тем изменяется во времени и состав дистиллята, который обедняется НК но мере протекания процесса. В связи с этим отбирают несколько фракций дистиллята, имеющих различный состав. Простая перегонка, проводимая с получением конечного продукта разного состава, называется фракционной, или дробной, перегонкой. В периодически действующей установке дли фракционной перегонки (рисунок 1) исходную смесь загружают в перегонный куб 1, снабженный змеевик ом для обогрева, и доводят до кипения.

Пары отводят в конденсатор-холодильник 2. Фракции дистиллята поступают через смотровой фонарь 3 в отдельные сборники 4 – 6. По окончании операции остаток сливают из куба, после чего в него вновь загружают разделяемую смесь. Для составления материального баланса простой перегонки примем, что в кубе в некоторый момент времени τ содержится L кг перегоняемой смеси, имеющей текущую концентрацию х (по низкокипящему компоненту НК). Количество НК В жидкости в этот момент равно L_x. Пусть за бесконечно малый промежуток времени dτ испарится dL кг смеси и концентрация жидкости в кубе уменьшится на величину dx.При этом образуются dL кг пара, равновесного с жидкостью и имеющего концентрацию у*, количество НК в паре будет равно dLу*. Соответственно остаток жидкости в кубе составит (L-dL), кг,а ее концентрация будет (x-dx). Тогда материальный баланс по НК выразится уравнением: . Раскрывая скобки и пренебрегая произведением dLdx как бесконечно малой величиной второго порядка, после разделения переменных получим Это дифференциальное уравнение должно быть проинтегрировано в пределах изменения количества жидкости в кубе от начального L=F до конечного L=W (где F – количество исходной смеси или питания, и W – количество остатка) и соответствующего падения ее концентрации от x_F до x_W. Средней состав (x_Dср) получаемого дистиллята рассчитывают из уравнения материального баланса по низкокипящему компоненту: 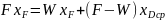Расчет простой перегонки обычно имеет целью определить количество жидкости, которое необходимо перегнать для того чтобы получить в кубе остаток заданного состава и дистиллят требуемого среднего состава. Простую перегонку проводят при атмосферном давлении или под вакуумом, присоединяя сборники дистиллята к источнику вакуума. Применение вакуума дает возможность разделить термически малостойкие смеси и, вследствие понижения температуры кипения раствора, использовать для обогрева куба пар более низких параметров.

79. Рабочие линии ректификационной колонны и их построение.

Зависимость является уравнением рабочей линии укрепляющей части колонны.

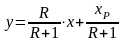
Х – текущая концентрация в жидкой фазе распределяемого компонента; R=Ф/P – флегмовое число, представляющее собой отношение количества флегмы к количеству дистиллята; X_P-содержание низкокипящего компонента в дистилляте. В этом уравнении – тангенс угла наклона рабочей линии к оси абсцисс, а 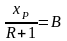– отрезок, отсекаемый рабочей линией на оси ординат диаграммы x-y рис.

Исчерпывающая часть колонны.

Зависимость представляет собой уравнение рабочей линии исчерпывающей части колонны. В этом уравнении (R+f)/(R+1)=tg α =A – тангенс угла наклона рабочей линии к оси ординат, а (1-f)/(R+1)=B – отрезок, отсекаемый рабочей линией на оси абсцисс.

Умножив числитель и знаменатель выражений для А и B (для укрепляющей части колонны) на количество дистиллята Р, можно заменить, что они представляют собой отношение количеств жидкой и паровой фаз, или удельный расход жидкости, орошающей данную часть колонны.

Рисунок – Построение рабочих линий ректификационной колонны на y – х – диаграмме

80,81. Флегмовое число. Определение его минимального и оптимального значения.

Отношение количества кмолей флегмы Ф, приходящихся на 1 кмоль отбираемого дистиллята Р, называют флегмовым числом R (т.е. R=Ф/Р). Понятие о флегмовом числе введено для удобства анализа и расчета процесса ректификации.

Практически флегмовое число не бывает задано, и при расчетах ректификационных колонн надо правильно это число подобрать. Между флегмовым числом и числом ступеней изменения концентраций существует определенная зависимость.

Минимальное значение флегмового числа графически определяется так: из точки а (на диагонали диаграммы), имеющей абсциссу , проводят прямую через точку пересечение линии с кривой равновесия, до пересечения с ординатой в точке . Подставляя полученное (по масштабу) значение отрезка 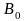в уравнение

, получают минимальное значение флегмового числа

Минимальное значение флегмового числа можно найти и аналитически. Из диаграммы следует, что откуда

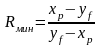
Если бы линии рабочих концентраций пересекались в точке на диагонали диаграммы, т.е. если бы направление линий рабочих концентраций совпадало с диагональю диаграммы, то отрезок на оси ординат В=0 и по уравнению флегмовое число должно бы быть бесконечно большим. При этом число ступеней изменение концентраций было бы минимальным. Практически такой случай может иметь место при работе ректификационной колонны без отбора дистиллята, т.е. количество пара, протекающего снизу вверх по колонне = флегмовому числу.

На практике линии рабочих концентраций должны пересекаться на диаграмме в точке 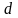, лежащей по линии ниже кривой равновесия и выше диагонали, и действительное флегмовое число должно быть больше минимального. В зависимости от условий ректификации и свойств разделяемой смеси ректификационные колонны работают при флегмовом числе 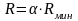(рабочее(действительное) число флегмы) где 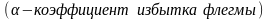_. При расчетах ректификационных колонн рабочее число флегмы часто определяется по формуле _. 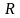Характер зависимости между флегмовым числом и числом ступеней изменения концентрации колонны показан на рисунке

Действительное флегмовое число определяют, строя такую зависимость для заданных условий перегонки. Из графика видно, что, начиная с некоторой величины , дальнейшее уменьшение флегмового числа проводит к резкому увеличению числа ступеней изменения концентрации. Поэтому на кривой выбирают точку М, лежащую в непосредственной близости от участка, соответствующего указанному выше возрастанию числа ступеней изменения концентрации.

Во всех случаях при выборе флегмового числа необходимо учесть, что с увеличением флегмового числа число изменения концентрации, а следовательно, и высота колонны уменьшается, но при этом пропорционально возрастает расход тепла на ректификацию, и, наоборот, с уменьшением флегмового числа расход тепла соответственно уменьшается, но при этом колонна должна иметь большее число ступеней изменения концентрации или большую высоту.

85.Сушка. Общая характеристика процесса и т.д..Сушка представляет собой процесс удаления влаги из твердых влажных материалов путем её испарения и отвода образующихся паров. Сушка является наиболее распространённым способом удаления влаги из твёрдых и пастообразных материалов, а также в ряде случаев и из суспензий.

Этот процесс широко используется в химической технологии. Удаление влаги позволяет удешевить транспортировку материалов, придать им определенные свойства (например, уменьшить слеживаемость удобрений), уменьшить коррозию аппаратуры и трубопроводов при хранении или последующей их обработке

В химической промышленности в основном применяется искусственная сушка материалов в специальных сушильных установках, так как естественная сушка – процесс довольно длительный.

По способу передачи тепла различают: конвективную, контактную, терморадиационную, высокочастотную и сублимационную сушку.

При конвективном способе сушки тепло для процесса передаётся от газообразного теплоносителя (нагретого воздуха, дымовых газов или их смеси) при непосредственном соприкосновении его с поверхностью высушиваемого материала.

При контактной сушке тепло передаётся материалу от нагретой плоской или цилиндрической поверхности.

При терморадиационном способе сушки передача тепла осуществляется за счёт радиационного излучения, основную часть спектра которого (около 80%) занимают инфракрасные лучи. Через

При высокочастотном способе сушки высушиваемый материал подаётся в поле токов высокой частоты, где под воздействием этого поля полярные молекулы (особенно Н₂О), стремясь ориентироваться вдоль направления поля, вынуждены совершать колебательные движения, в результате чего происходит разогрев материала.

При сублимационном способе сушки влагу удаляют из твёрдых материалов путём возгонки (сублимации), т.е. влагу переводят из твёрдой фазы в паровую, минуя жидкое состояние. Количество тепла, передаваемого от газообразного сушильного агента жидкости путём конвекции при температуре газа t_Г, превышающей температуру материала t_М, составит :

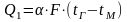
Количество испаряющейся жидкости (М) определяется уравнением:

,

где: К – коэффициент массопередачи;

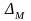- движущая сила процесса массопередачи.

79.Виды связи влаги с материалом.Методы ее удаленияМеханизм процесса сушки в значительной степени определяется формой связи влаги с материалом: чем прочнее эта связь, тем труднее протекает процесс сушки. При сушке связь влаги с материалом нарушается. Предложена следующая классификация форм связи влаги с материалом: химическая, физико-химическая,физико-механическая.Химически связанная влага наиболее прочно соединена с материалом в определенных (стехиометрических) соотношениях и может быть удалена только при нагревании материала до высоких температур или в результате проведения химической реакции. Эта влага не может быть удалена из материала при сушке. В процессе сушки удаляется, как правило, только влага, связанная с материалом физико-химически и механически. Наиболее легко может быть удалена механически связанная влага, которая, в свою очередь, подразделяется на влагу макрокапилляров и микрокапилляров (капилляров со средним радиусом приблизительно больше и меньше 10° см). Макрокапилляры заполняются влагой при непосредственном соприкосновении ее с материалом, в то время как в микрокапилляры влага поступает как при непосредственном соприкосновении, так и в результате поглощения ее из окружающей среды. Влага макрокапилляров свободно удаляется не только сушкой, но и механическими способами. Физико-химическая связь объединяет два вида влаги, отличающихся прочностью связи с материалом: адсорбционно и осмотически связанную влагу. Первая прочно удерживается на поверхности и в порах материала. Осмотически связанная влага, называемая также влагой набухания, находится внутри клеток материала и удерживается осмотическими силами. Адсорбционная влага требует для своего удаления значительно большей затраты энергии, чем влага набухания. Присутствие этих видов влаги особенно характерно для коллоидных и полимерных материалов.Сушка топочными газами. В настоящее время все более широкое распространение приобретает сушка топочными газами, используемыми для сушки не только неорганических, но и органических материалов. Это объясняется в первую очередь тем, что температура топочных газов значительно выше температуры воздуха, нагреваемого перед сушкой. В результате влагопоглощающая способность газов во много раз больше влагопоглощающей способности воздуха и соответственно больше потенциал сушки.В качестве сушильного агента применяются газы, полученные либо сжиганием в топках твердого, жидкого или газообразного топлива либо отработанные газы котельных, промышленных печей или других установок. Используемые для сушки газы должны быть продуктами полного сгорания топлива и не содержать золы и сажи, загрязняющих высушиваемый материал в условиях конвективной сушки. С этой целью газы подвергаются сухой или мокрой очистке перед поступлением в сушилку. Обычно температура топочных газов превышает предельно допустимую для высушиваемого материала и поэтому их разбавляют воздухом для получения сушильного агента с требуемой температурой.Конструкции сушилок очень разнообразны и отличаются по ряду признаков: по способу подвода тепла (конвёктивные, контактные и др.), по виду используемого теплоносителя (воздушные, газовые, паровые), по величине давления в сушильной камере (атмосферные и вакуумные), по способу организации процесса (периодические и непрерывные), а также по взаимному направлению движения материала и сушильного агента в конвективных сушилках (прямоток, противоток, перекрестный ток). Это крайне затрудняет обобщающую классификацию сушилок.

95.Кинетика сушки.

Для расчёта сушилок необходимо знать скорость сушки, которая определяется кол-вом влаги W, испаряемой с единицы поверхности F высушиваемого материала за единицу времени. Т.е. U=W/F_τ кг/м²∙сек, где τ – время сушки, сек.

Зная скорость сушки, определяют продолжительность периодического процесса сушки или поверхность высушиваемого материала при сушке непрерывным способом и устанавливают габаритные размеры сушильных аппаратов.

Движущаяся сила процесса определяется разностью давлений р_м-р_п, т.е. разностью давления паров влаги у поверхности материала р_м и парциального давления паров в воздухе (или чистого пара) р_п.

Различают два периода сушки: период постоянной скорости и период падающей скорости процесса.

В течении первого периода влага испаряется со всей поверхности влажного материала так же, как она испаряется с зеркала испарения некоторого объёма жидкости. В этом периоде скорость сушки постоянна и определяется лишь скоростью внешней диффузии, т.е. диффузии паров влаги с поверхности материала в окружающую среду.

Во втором периоде скорость сушки определяется внутренней диффузией – перемещением влаги изнутри материала к его поверхности. С начала второго периода поверхность подсохнувшего материала начинает покрываться коркой и поверхность испарения влаги постепенно уменьшается, что приводит к увеличению сопротивления внутренней диффузии и к непрерывному уменьшению скорости сушки.

В зависимости от толщины и структуры некоторых материалов испарение влаги с их поверхности в конце второго периода прекращается вовсе и происходит в глубине материала. Поэтому, в соответствии с характером удаления влаги, второй период сушки часто складывается из двух стадий: стадии равномерно падающей скорости и стадии неравномерно падающей скорости.

Двум основным периодам предшествует некоторый период прогрева материала до температуры сушки.

Кинетика сушки определяется обычно путём взвешивания образцов материала в начале сушки и через определённые промежутки времени. По весу образцов рассчитывают абсолютную влажность материала в разли чные моменты и строят кривую зависимости абсолютной влажности ω_а от времени τ, которая называется кривой сушки (АВК₁К₂С). По этой кривой можно определить скорость сушки.

Скорость сушки, характеризующаяся изменением абсолютной влажности в единицу времени, может быть найдена для каждого данного момента, как тангенс угла наклона кривой сушки (например, tgα2 для точки К₂ на рис.21-13)Найденные значения скорости сушки наносят на график, как функцию абсолютной влажности, и получают кривую скорости сушки (рис. 21-14). Графическое изображение процесса в виде кривых сушки и кривых скорости сушки дает возможность установить различные периоды его протекания.Рассматривая кривые на рис. 21-13 и 21-14, можно различить перечисленные выше периоды сушки материала.

Период прогрева материала (отрезок АВ на рис. 21-14) является, как правило, кратковременным и характеризуется неустановившимся состоянием процесса. За этот период температура материала повышается до температуры мокрого термометра t_M, но его влажность x_нач, снижается незначительно. Скорость сушки возрастает и к концу периода прогрева достигает максимальной величины.

В период постоянной скорости (прямолинейный отрезок ВК₁) скорость процесса является наибольшей, температура материала t_M = const.Начальная точка Kt периода падающей скорости (отрезок К₁К₂С) называется первой критической точкой, а влажность материала х_кp, в этой точке — первой критической влажностью.

Период падающей скорости состоит, в свою очередь, из двух стадий: равномерно падающей скорости (прямолинейный отрезок K₁K₂ на рис.21-14) и неравномерно падающей скорости (кривая К₂ С).

Точка К₂ называется второй критической точкой, а соответствующая ей влажность материала — второй критической влажностью w''_кр .К концу второго периода температура материала повышается и достигает температуры воздуха t_B или среды, окружающей материал. Одновременно влажность материала снижается до равновесной по всей его толщине. С момента достижения равновесной влажности скорость сушки становится равной нулю. При дальнейшем пребывании материала в сушилке его влажность остается постоянной (отрезок CD на рис. 21-13)

Длительность сушки материала достаточно точно можно установить только опытным путем. Общую продолжительность процесса определяют расчетом как сумму длительности сушки в период постоянной скорости и длительности ее в период па­дающей скорости, принимая, что падение скорости сушки во втором периоде происходит прямолинейно.

Длительность сушки в отдельные периоды определяют по следующим •формулам:

в период постоянной скорости

в период падающей скорости

W,

Соответственно общая продолжительность сушки может быть приближенно определена по уравнению

где w₁ w₂ и w_p—начальная, конечная и равновесная влажность материала» кг влаги на 1 кг сухого вещества; w'_кp — первая критическая влажность материала (в конце первого периода сушки).Величина С называется коэффициентом сушки и выражается количеством кг испаренной влаги в сек, приходящимся на 1 кг сухого вещества.

Обозначая количество испаренной влаги W кг, количество сухого вещеcтва в высушиваемом материале G_сух, кг и время сушки τ,сек, получим, следующее выражение для коэффициента сушки:

где β — коэффициент массоотдачи в газовой фазе, кг/м²•сек•кг/кгf— удельная поверхность сухого вещества, м²/кг абсолютно сухого вещества

∆_ср— средняя движущая сила, равная средней разности влагосодержания воздуха в насыщенном и рабочем состояниях ∆_ср. = (x*- x)_ср

97,98,99,100,101. Классификация сушилок

По способу подвода тепла:

1. Конвективные

2. Контактные

3. Радиационные

4. Высокочастотные

По виду теплоносителя:

1. Воздушные

2. Паровые

По давлению:

1. Атмосферные

2. Вакуумные

По организации процесса во времени:

1. Периодические

2. Непрерывные

По взаимному направлению движения сушильного агента и материала:

1. Прямоточные

2. Противоточные

3. Перекрестные

4. Смешанные

По конструктивным признакам:

1. Камерные

2. Ленточные

3. Барабанные

4. Распылительные

5. Вальцовые

6. Радиационные

7. Высокочастотные

8. Сушилки кипящего слоя