Б) Пространственные отношения в природе

для определения положения какого-либо события в пространстве требуется произвести три измерения и указать три числа, называемые пространственными координатами, например, высоту над поверхностью Земли, широту и долготу (физическое пространство трехмерно).

Рассмотрим сначала пространственные отношения в одном измерении, например, вдоль оси X. С этой целью введем эталонный объект — масштаб (линейку), в качестве которого можно использовать любой материальный объект (твердое тело), размеры которого можно считать неизменными. Положение материального объекта вдоль оси X может быть указано в соответствии с правилом «ближе–дальше», после чего ему сопоставляется геометрическая точка х_А. За начало отсчета на такой оси можно выбрать произвольную точку х₀ = 0. Пространственные координаты одного и того же события относительны: они зависят от выбора начала отсчета пространственных координат и поэтому сами по себе не могут служить объективными характеристиками пространственных отношений. Расстояние между двумя точками на этой оси, отвечающими положениям двух различных материальных объектов достаточно малого размера, уже не зависит от выбора начала отсчета. Иными словами, в данный момент времени расстояние вдоль оси Х инвариантно (неизменно) по отношению к выбору начала отсчета пространственных координат, поэтому его можно выбирать в качестве объективной характеристики пространственных отношений вдоль оси Х. В этом отражается важнейшее свойство пространства — егооднородность. Это означает физическое равноправие всех точек в пространстве.

В трехмерном пространстве помимо того, что для каждого объекта необходимо задавать не одну, а три координаты, для описания пространственных отношений двух материальных объектов необходимо указывать направление от одного материального объекта к другому. Для этих целей служит вектор , длина которого равна расстоянию между объектами, а его направление в заданной системе координат характеризуется направляющими углами с осями координат.

Разности пространственных координат двух объектов зависят от выбора направлений осей координат. А расстояние между объектами и углы между двумя прямыми не изменяются при повороте координатных осей. В этом находит отражение еще одно важнейшее свойство пространства — его изотропность (физическое равноправие всех направлений в пространстве).

пространство однородно и изотропно. время однородно. Следовательно, ни в пространстве, ни во времени нет особых (выделенных, заметных глазу) точек и направлений. Для описания любых изменений в природе (в том числе и механического движения) необходимо построить искусственную систему, относительно которой определяется положение и время протекания процесса – систему отсчета (СО). Система отсчета состоит из: тела отсчета, связанной с ним системы координат и указания о начале отсчета времени (часов).

3.1.5.

Классические преобразования галилея.

Классические преобразования Галилея – формулы преобразований координат и времени при переходе из одной ИСО в другую ИСО:

Рис.1

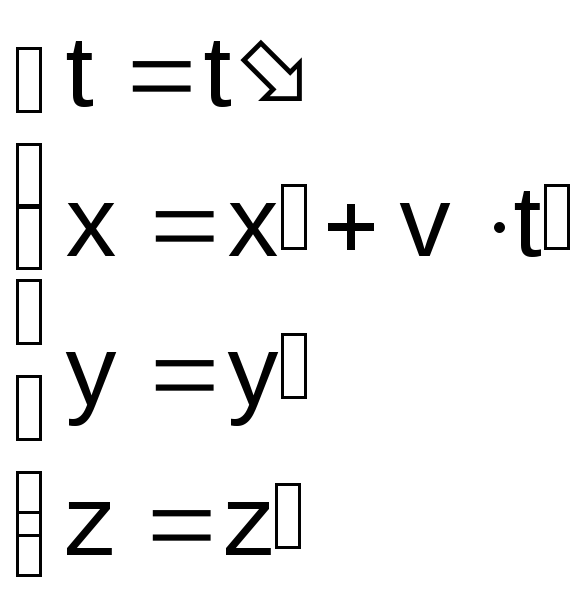
Закон сложения скоростей Галилея – формула преобразования скорости при переходе из одной ИСО в другую ИСО:

.

3.1.6.

Законы сохранения в классической механике.

законы сохранения выполняются в замкнутых системах взаимодействующих тел.

Система называется замкнутой, если на систему не действуют внешние силы.

Импульс – векторная физическая величина, количественно характеризующая запас поступательного движения:

.

Закон сохранения импульса системы материальных точек (м.т.): в замкнутых системах м.т. полный импульс сохраняется

,

или

,

где – скорость i-й материальной точки до взаимодействия;– ее скорость после взаимодействия.

3.1.7.

Момент импульса – физическая векторная величина, количественно характеризующая запас вращательного движения.

,

– импульс материальной точки, – радиус-вектор материальной точки.

Закон сохранения момента импульса: в замкнутой системе суммарный момент импульса сохраняется:

.

3.1.8.

Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией.

Энергия – скалярная физическая величина, являющаяся наиболее общей характеристикой состояния системы.

Состояние системы определяется ее движением и конфигурацией, т. е. взаимным расположением ее частей. Движение системы характеризуется кинетической энергией K, а конфигурация (нахождение тела в потенциальном поле сил) – потенциальной энергией U.

Полная энергия определяется как сумма:

E = K + U + E_внутр,

где E_внутр – внутренняя энергия тела.

Кинетическая и потенциальная энергии в сумме составляют механическую энергию.

Формула Эйнштейна (взаимосвязь энергии и массы):

Е = m^.c².

В системе отсчета, связанной с центром масс системы м.т., m = m₀ – масса покоя, а Е = Е₀ = m₀^.c² – энергия покоя.

Внутренняя энергия определяется в системе отсчета, связанной с самим телом, то есть внутренняя энергия является одновременно и энергией покоя.

Кинетическая энергия – это энергия механического движения тела или системы тел. Релятивистская кинетическая энергия определяется по формуле

.

При малых скоростях v<<c или  << 1

.

Потенциальная энергия – скалярная физическая величина, характеризующая взаимодействие тел с другими телами или с полями.

Примеры:

• потенциальная энергия упругого взаимодействия

;

• потенциальная энергия гравитационного взаимодействия точечных масс

;

Закон сохранения энергии: полная энергия замкнутой системы материальных точек сохраняется

.

При отсутствии диссипации (рассеяния) энергии сохраняются и полная и механическая энергии. В диссипативных системах полная энергия сохраняется, а механическая энергия не сохраняется.

3.1.9.

в наше время установлены связи между свойствами пространства–времени и законами сохранения.

1. Закон сохранения импульса является следствием однородности пространства.

2. Закон сохранения момента импульса является следствием изотропности пространства.

3. Закон сохранения энергии является следствием однородности времени.

3.2.1.

Материя. Вещество и поле.

Механическая картина мира знала только один вид материи — вещество, состоящее из частиц, имеющих массу. Первоначально считалось, что тела взаимодействуют на расстоянии, без каких бы то ни было промежуточных материальных посредников. Затем была выдвинута новая точка зрения: взаимодействие передается с помощью особого материального посредника. В результате в естествознании начало утверждаться понимание того, что пространство между телами никогда не является пустым: оно заполнено материей в форме силового поля. Поле является переносчиком взаимодействия тел. Каждое тело «узнает» о существовании других тел только через окружающие его поля.

В XIX веке к числу свойств частиц стали прибавлять электрический заряд. И хотя масса, как считалось, была у всех частиц, а заряд — только у некоторых, обладание электрическим зарядом было признано таким же фундаментальным, важнейшим их свойством, как и масса. Между электрически заряженными телами, между намагниченными телами, между телами, по которым текут токи, действуют силы, называемые электромагнитными. В начале 19 века английский химик и физик Майкл Фарадей (1791-1867) ввел в науку понятие электромагнитного поля – материальной среды, являющейся переносчиком электромагнитного взаимодействия. Модель электромагнитного поля была введена для объяснения механизма дальнодействия. Фарадею удалось показать опытным путем, что между магнетизмом и электричеством существует прямая динамическая связь. Тем самым он впервые объединил электричество и магнетизм, признал их одной и той же «силой» природы.

Математическую разработку идей Фарадея предпринял выдающийся английский ученый Джеймс Кларк Максвелл (1831-1879). Его основной работой, заключавшей в себе математическую теорию электромагнитного поля, явился «Трактат об электричестве и магнетизме», изданный в 1873 году. Введение Фарадеем понятия электромагнитного поля и математическое определение его законов, данное в уравнениях Максвелла, явились самыми крупными событиями в физике со времен Галилея и Ньютона.

Эта теория существенно изменила представления о картине электрических и магнитных явлений, объединив их в единое целое.

Решающую роль в победе максвелловской теории сыграл немецкий физик Генрих Рудольф Герц (1857-1894). Именно ему по поручению Гельмгольца²¹ (Герц был его любимым учеником) довелось проверить экспериментально теоретические выводы Максвелла. В 1886 году Герц продемонстрировал «беспроволочное распространение» электромагнитных волн. Он смог также доказать принципиальную тождественность полученных им электромагнитных переменных полей и световых волн.

С тех пор механические представления о мире были существенно поколеблены. Ведь любые попытки распространить механические принципы на электрические и магнитные явления оказались несостоятельными. Поэтому естествознание вынуждено было, в конце концов, отказаться от признания особой, универсальной роли механики. Механическая картина мира начала сходить с исторической сцены, уступая место новому пониманию физической реальности.

3.2.2.

Электрические заряды и их свойства.

Источником электромагнитного поля является электрический заряд.

Электрический заряд – это свойство некоторых элементарных частиц вступать в электромагнитное взаимодействие.

Свойства электрического заряда:

1. Электрический заряд может быть положительным и отрицательным (принято считать, что протон заряжен положительно, а электрон – отрицательно).

2. Электрический заряд квантован. Квант электрического заряда – элементарный электрический заряд (е = 1,610^–19 Кл). В свободном состоянии все заряды кратны целому числу элементарных электрических зарядов:

3. Закон сохранения заряда: суммарный электрический заряд замкнутой системы сохраняется во всех процессах, происходящих с участием заряженных частиц:

q₁ + q₂ +...+ q_N = q₁^* + q₂^*+...+ q_N^*.

4. релятивистская инвариантность: величина полного заряда системы не зависит от движения носителей заряда (заряд движущейся и покоящейся частиц одинаков). Иными словами – во всех ИСО величина заряда любой частицы или тела одинакова.

3.2.3. 3.2.4.

Описание электромагнитного поля.

Заряды взаимодействуют друг с другом (рис.1). Величина силы, с которой заряды одного знака отталкиваются друг от друга, а заряды разного знака притягиваются друг к другу, определяется с помощью эмпирически установленного закона Кулона:

.

Здесь , – электрическая постоянная.

Рис.1

А каков механизм взаимодействия заряженных тел? Можно выдвинуть такую гипотезу: тела, обладающие электрическим зарядом, порождают электромагнитное поле. В свою очередь, электромагнитное поле воздействует на другие заряженные тела, находящиеся в этом поле. Возник новый материальный объект – электромагнитное поле. Его необходимо описать. Как? Для выбора модели электромагнитного поля нужно сконструировать такие величины, задание которых однозначно определяло бы свойства поля.

Исследуется электромагнитное поле с помощью «пробного» заряда. Каким он должен быть?

1. Он должен быть настолько мал, чтобы его собственное поле не искажало исследуемое поле;

2. Размеры тела, несущего пробный заряд, должны быть настолько малы, чтобы измеренные с его помощью характеристики поля можно было сопоставить с какой-то определенной точкой поля.

А какие величины характеризуют поле и сколько их? Для того чтобы выбрать величины, характеризующие электромагнитное поле необходимо основываться на опытных данных.

Опыт показывает, что в любом электромагнитном поле на неподвижный заряд действует сила, величина которой зависит только от величины заряда (величина силы пропорциональна величине заряда ) и его положения в поле. Можно каждой точке поля поставить в соответствие некоторый вектор, который является коэффициентом пропорциональности между силой, действующей на неподвижный заряд в поле, и зарядом. Тогда силу, с которой поледействует на неподвижный зарядможно определить по формуле:

.

Сила, действующая со стороны электромагнитного поля на неподвижный заряд, называется электрической силой . Векторная величина, характеризующая то состояние поля, которое обуславливает действие, называется электрической напряженностью электромагнитного поля.

Дальнейшие эксперименты с зарядами показывают, что вектор не характеризует электромагнитное поле полностью. Если зарядначать двигать, то появляется некоторая дополнительная сила, величина и направление которой никак не связаны с величиной и направлением вектора. Следовательно, для однозначного описания состояния электромагнитного поля, необходимо задать еще другие параметры. Какие это параметры? И сколько их? Добавочную силу, возникающую при движении заряда в электромагнитном поле, называют магнитной силой. Опыт показывает, что магнитная сила зависит от заряда и от величины и направления вектора скорости. Если двигать пробный заряд через какую-либо фиксированную точку поля с одной и той же по величине скоростью, но в разных направлениях, то магнитная сила каждый раз будет разной. Однако всегда. Дальнейший анализ экспериментальных фактов позволил установить, что для каждой точки электромагнитного поля существует единственное направлениеMN (рис.2), обладающее следующими свойствами:

1. Если двигать заряд по этому направлению с любой скоростью, то .

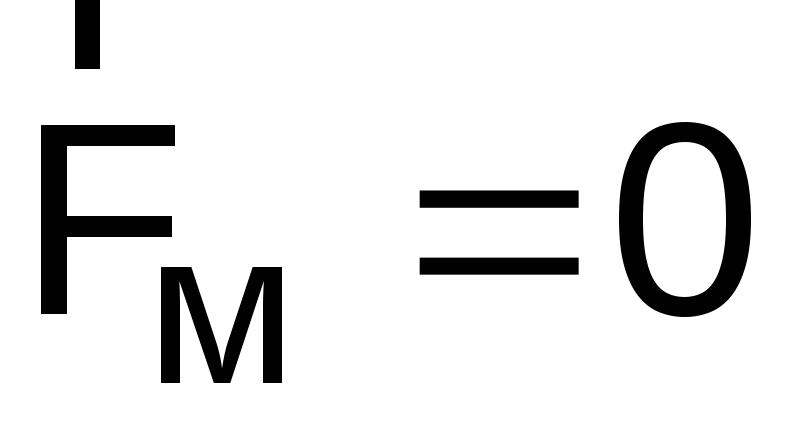2. Если скорость заряда составляет некоторый угол с этим направлением, то величина магнитной силы пропорциональна синусу этого угла .

3. При всевозможных движениях зарядавсегда перпендикулярна этому выделенному направлению, то есть всележат в одной плоскости перпендикулярнойMN.

Рис.2

Если вдоль направления MN направить некоторый вектор , имеющий смысл коэффициента пропорциональности между магнитной силой и произведением, то задание,иоднозначно характеризует то состояние поля, которое обусловливает появление. Векторназвали вектором электромагнитной индукции. Так каки, то

.

В электромагнитном поле на движущийся со скоростью заряд q действует электромагнитная сила Лоренца (рис.3):

.

Рис.3

Векторы и, то есть шестерка чисел, являются равноправными компонентами единого электромагнитного поля (компоненты тензора электромагнитного поля). В частном случае может оказаться, что всеили все; тогда электромагнитное поле сводится либо к электрическому, либо к магнитному полям.

Эксперимент подтвердил правильность построенной двухвекторной модели электромагнитного поля. В этой модели каждой точке электромагнитного поля задается пара векторов и. Построенная нами модель – модель непрерывного поля, так как функциии, описывающие поле, являются непрерывными функциями координат.

Теория электромагнитных явлений, использующая модель непрерывного поля, называется классической.

В действительности поле, как и вещество, дискретно. Но это начинает сказываться лишь на расстояниях, сравнимых с размерами элементарных частиц. Дискретность электромагнитного поля учитывается в квантовой теории.

3.2.5.

Принцип суперпозиции.

Поля принято изображать с помощью силовых линий.

Силовая линия – это линия, касательная к которой в каждой точке совпадает с вектором напряженности поля.

Для точечных неподвижных зарядов картина силовых линий электростатического поля показана на рис. 6.

Рис. 6

Вектор напряженности электростатического поля, создаваемого точечным зарядомопределяется по формуле (рис.7 а и б)

.

Рис. 7

магнитное поле существует и проявляется только в системе отсчета, относительно которой электрический заряд движется.

Движущийся электрический заряд создает и электрическое и магнитное поля (единое электромагнитное поле). Силовая характеристика магнитного поля – индукция – связана с напряженностью электрического полясоотношением

.

Поэтому индукция магнитного поля медленно движущегося точечного заряда равна

.

Силовая линия магнитного поля строится так, чтобы в каждой точке силовой линии векторбыл направлен по касательной к этой линии. Силовые линии магнитного поля замкнуты (рис.8). Это говорит о том, что магнитное поле – вихревое поле.

Рис. 8

А если поле создает не один, а несколько точечных зарядов? Влияют ли заряды друг на друга или каждый из зарядов системы вносит свой вклад в результирующее поле независимо от остальных? Будет ли электромагнитное поле, создаваемое i-м зарядом в отсутствии остальных зарядов таким же, как и поле создаваемое i-м зарядом в присутствии остальных зарядов?

Принцип суперпозиции: электромагнитное поле произвольной системы зарядов есть результат сложения полей, которые создавались бы каждым из элементарных зарядов этой системы в отсутствии остальных:

и .

3.2.6.

Законы электромагнитного поля

Законы электромагнитного поля сформулированы в виде системы уравнений Максвелла.

Первое уравнение Максвелла для электростатического поля:

.

Из первого уравнения Максвелла следует, что электростатическое поле – потенциальное (сходящееся или расходящееся) и его источником являются неподвижные электрические заряды.

Второе уравнение Максвелла для магнитостатического поля:

.

Из второго уравнения Максвелла следует, что магнитостатическое поле – вихревое не потенциальное и не имеет точечных источников.

Третье уравнение Максвелла для электростатического поля:

.

Из третьего уравнения Максвелла следует, что электростатическое поле не вихревое.

В электродинамике (для переменного электромагнитного поля) третье уравнение Максвелла:

,

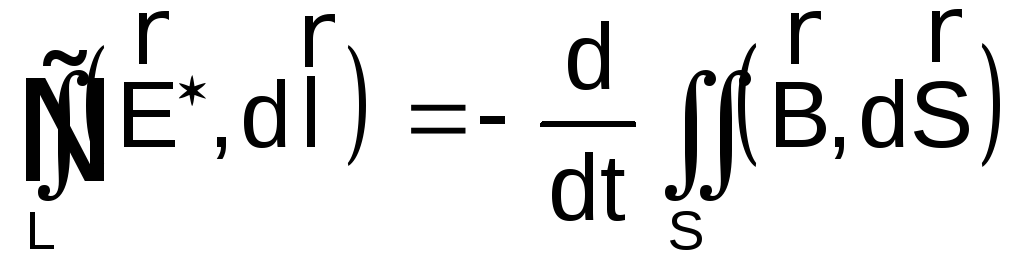т. е. электрическое поле не потенциальное (не кулоновское), а вихревое и создается переменным потоком вектора индукции магнитного поля.

Четвертое уравнение Максвелла для магнитостатического поля

,

Из четвертого уравнения Максвелла в магнитостатике следует, что магнитное поле – вихревое и создается постоянными электрическими токами или движущимися зарядами. Направление закрученности силовых линий магнитного поля определяется по правилу правого винта (рис.9).

Р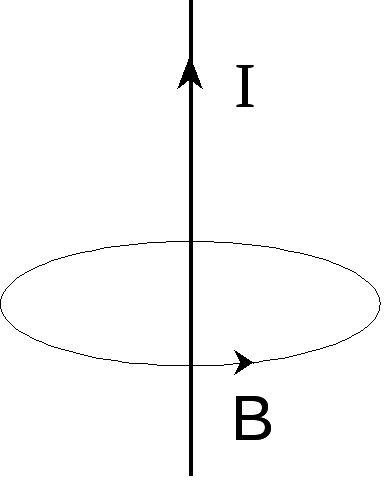ис.9

В электродинамике четвертое уравнение Максвелла:

.

Первое слагаемое в этом уравнении есть ток проводимости I, связанный с движением зарядов и создающий магнитное поле.

Второе слагаемое в этом уравнении есть "ток смещения в вакууме", т. е. переменный поток вектора напряженности электрического поля.

Основные положения и выводы теории Максвелла следующие.

•Изменение во времени электрического поля ведет к появлению магнитного поля и наоборот. Следовательно, существуют электромагнитные волны.

•Передача электромагнитной энергии происходит с конечной скоростью. Скорость передачи электромагнитных колебаний равна скорости света 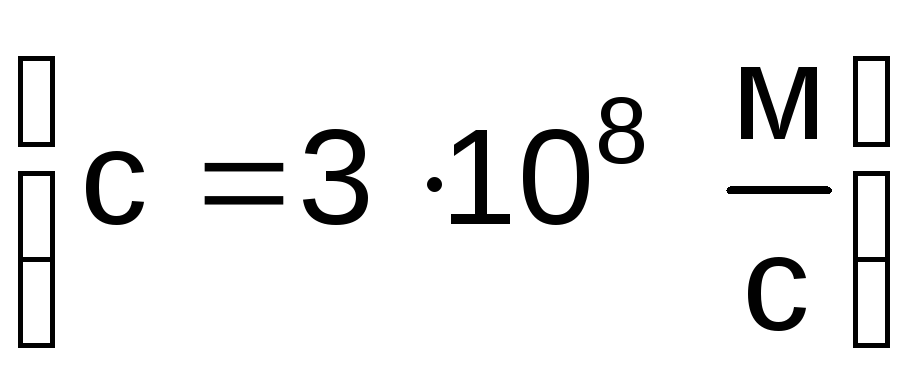. Из этого следовала принципиальная тождественность электромагнитных и оптических явлений.

3.3.1.

Предпосылки для создания теории относительности.

Цель физики – изучение того, что происходит во Вселенной и построение простейшей системы постулатов, охватывающих и объясняющих все наблюдаемые явления.

Первой теорией, которая объясняла все существующие к моменту ее создания явления природы, была механика Ньютона. Основоположником экспериментального естествознания был итальянский физик Галилео Галилей (1562 – 1642). Главная заслуга Галилея состоит в том, что он сформулировал принцип относительности и написал уравнения преобразования координат и скорости при переходе из одной ИСО в другую.

Принцип относительности Галилея.

• Во всех ИСО механические процессы протекают одинаково.

• Никакой механический эксперимент не позволяет нам выделить из совокупности ИСО какую-либо одну преимущественную систему отсчета.

Отсюда следует:

1. Все ИСО равноправны;

2. Не бывает абсолютного покоя и абсолютного движения.

Преобразования координат и скорости Галилея.

Они устанавливают инвариантность длины, времени и ускорения относительно преобразований Галилея. Это означает, что в системах координат К и К^’

.

Большинство явлений, происходящих в природе, подтверждали справедливость построенной механистической картины мира, в основе которой лежали принцип относительности Галилея и преобразования координат и скорости Галилея.

Ньютон ввел в науку математику. Он создал дифференциальное исчисление. Используя дифференциальное исчисление, Ньютон показал, что движение можно описать формулами. Формула – это удобный способ краткой записи физических процессов.

Ньютон ввел в науку понятие теории. Любая теория должна основываться на небольшом числе постулатов (чем их меньше – тем лучше). На базе этих постулатов (законов) можно делать различные предсказания.

Теория должна допускать проверку опытом.

Эта система существует до тех пор, пока не находятся такие явления, которые невозможно объяснить с помощью этой системы постулатов. Тогда создается новая система постулатов, объясняющая все явления природы. Старая система постулатов остается лишь частным случаем новой.

Какие же явления привели Эйнштейна к созданию новой системы постулатов – специальной (СТО), а затем и общей (ОТО) теории относительности?