3. Из уравнений ото следует расширение Вселенной, которое было подтверждено экспериментально (красное смещение).

Решения своих уравнений Эйнштейн не нашел. Он только показал, что при они сводятся к уравнениям Ньютона. То есть классическая механика является частным случаем ОТО.

В1915-1916 годах немецкий астроном Карл Шварцшильд решил уравнение Эйнштейна для сферического распределения масс. Из его решений следовало, что при очень большой плотности материи пространство искривляется так сильно, что становится похожим на воронку. А куда ведет этот тоннель? Может быть в другую Вселенную? Расчеты показали, что для прохождения по тоннелю нужны скорости большие скорости света. А ОТО не разрешает двигаться со скоростями большими скорости света.

Во времена Эйнштейна были известны два поля: гравитационное и электромагнитное. Он пытался построить единую теорию поля, из которой получались бы все известные к тому времени уравнения. Сделать ему это не удалось. Может быть для этого нужна новая математика? (Ньютон создал механику после рождения дифференциального исчисления. Эйнштейн создал ОТО после создания тензорного исчисления).

3.5.1.

Уравнение волны.

Распространяющиеся в пространстве колебания вещества или поля называются волной.

Колебания вещества порождают упругие волны (частный случай – звук).

Колебания электромагнитного поля порождают электромагнитные волны (частный случай – свет).

Как записать уравнение волны?

Пусть кусочек шнура расположенный в точке О совершает колебания, происходящие по закону косинуса

.

Пусть точка некоторая В находится на расстоянии х от точки О. для того, чтобы волна, распространяющаяся со скоростью v, дошла до нее требуется время

.

Тогда в точке В колебания начнутся позже на . То есть

.

Выражение, стоящее под знаком косинуса называется фазой волны.

.

фазы точек шнура В и С, находящихся на различных расстояниях иот источника волны (точки О), будут различны

Разность фаз этих колебаний

.

Говорят, что колебания в точках В и С происходят в фазе, если . Если, то колебания в точках В и С происходят в противофазе.

Расстояние между двумя ближайшими точками, колеблющимися в фазе, называется длиной волны .

.

Так как и, то

.

Следовательно, длина волны – это путь, проходимый волной за один период колебания.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.

Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.

Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

3.5.4. .3.5.3 Эффект Доплера.

При относительном движении источника и приемника в среде частота  принимаемой упругой волны отличается от частоты ₀ испускаемой упругой волны. Тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении.

Эффектом Доплера называется изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника относительно друг друга.

Поскольку упругие волны распространяются только в среде, внутри которой могут двигаться источник и приемник, рассматривают не только их относительное движение, но и их движение относительно среды.

.

Верхние знаки при сближении источника и приемника, нижние – при удалении.

При приближении приемника к источнику >₀, а при удалении приемника от источника <₀.

Поперечный эффект Доплера в акустике (для звуковых волн) отсутствует.

Эффект Доплера наблюдается также и при движении относительно друг друга источника и приемника электромагнитных волн. Так как особой среды, служащей носителем электромагнитных волн, не существует, то частота световых волн, воспринимаемых приемником (наблюдателем), зависит только от относительной скорости v источника и приемника.

.

– угол между вектором скорости и направлением наблюдения, измеряемый в системе отсчета, связанной с наблюдателем.

Если (источник и приемник удаляются друг от друга по одной прямой), то

и . В этом случае наблюдается сдвиг в длинноволновую область – так называемое «красное смещение».

Если (источник и приемник приближаются друг к другу по одной прямой), то

и . В этом случае наблюдается сдвиг в коротковолновую область – так называемое «фиолетовое смещение».

Это так называемый продольный эффект Доплера. Он используется при исследовании атомов, молекул, космических тел. По характеру смещения спектральных линий определяется характер движения излучающих свет частиц или тел. Эффект Доплера получил широкое применение в радиолокации.

Если , то. Эта формула определяет так называемый поперечный эффект Доплера. Он наблюдается при движении приемника перпендикулярно линии, соединяющей его с источником. Этот эффект является чисто релятивистским (в акустике поперечный эффект Доплера не наблюдается). Его обнаружение служило еще одним подтверждением верности СТО.

3.5.5.

Принцип суперпозиции волн.

Каждая точка среды, до которой дошли две или более волн, будет принимать участие в колебаниях, вызванных каждой волной в отдельности. А каким будет результирующее колебание? Опыт показывает, что в одной и той же среде волны распространяются независимо друг от друга, если свойства среды не изменяются из-за процесса распространения волн (среда линейна). Для определения амплитуды результирующего колебания необходимо найти смещение, вызванное каждой волной, а затем их сложить. Как?

Принцип суперпозиции (наложения) волн:

• при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют;

• результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

3.5.6.

Интерференция волн.

Рассмотрим, каким будет результат сложения двух волн, приходящих в некоторую точку пространства (точку наблюдения) Р. Пусть волны, которые излучаются источникамиS₁ и S₂ имеют одинаковую частоту и амплитуду, начальные фазы равные нулю и разность фаз волн, приходящих в точку Р не зависит от времени. Такие волны называются когерентными. В точке Р волны, приходящие от источников S₁ и S₂ будут вызывать колебания частиц среды

Результирующее колебание в точке Р найдем как сумму

–разность хода волн, приходящих в точку Р.

Амплитуда колебаний, возникающих в точке Р, зависит от того, какова разность путей, проходимых каждой волной в отдельности от источника до точки Р .

Следовательно, в тех точках пространства, для которых , амплитуда возникающих колебаний будет максимальна и равна 2А. Это точки максимумов. Так как, то амплитуда колебаний будет максимальна в тех точках, для которых

.

в тех точках пространства, для которых , амплитуда возникающих колебаний будет минимальна и равна нулю. Это минимумы.амплитуда колебаний будет минимальна в тех точках, для которых

.

Условия максимумов и минимумов интерференции:

Максимумы: ;;.

Минимумы: ;;..

Явление перераспределения энергии, возникающее в результате сложения когерентных волн, называется интерференцией.

3.5.7.

Дифракция волн.

Явление огибания волнами препятствий называется дифракцией.

Любое отклонение распространения волн вблизи препятствий от законов геометрической оптики.

Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т.д.

Объяснить явление дифракции можно с помощью принципа Гюйгенса: каждая точка, до которой доходит волна, является источником вторичных волн (в однородной среде сферических), а огибающая этих волн задает положение волнового фронта в следующий момент времени.

А как определить амплитуду колебаний в любой точке, до которой дошла волна? Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн.

Принцип Гюйгенса–Френеля: каждый элемент волновой поверхности служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента.

.

Строго решить задачу с помощью принципа Гюйгенса–Френеля очень трудно. А как?

1. для каждой конкретной задачи следует определенным образом разбить фронт волны на участки (зоны Френеля);

2. эти участки рассматривать как самостоятельные одинаковые источники волн;

3. амплитуда волны в точке наблюдения определяется как результат интерференции от волн, которые якобы создаются зонами Френеля.

Результаты таких расчетов хорошо согласуются с результатами эксперимента.

В²² 1875 году американец Гопкинсон, рассматривая светящийся фонарь сквозь носовой платок, увидел систему темных полос. Они не изменяли своего положения при параллельном перемещении платка. Он сообщил об этом американскому астроному Риттенхаузу, который повторил опыт Гопкинсона. Риттенхауз усоверщенствовал метод и получил первую дифракционную решетку – 190 волосков на дюйм. В 1798 г. он опубликовал результаты.

4.1

Тепловое излучение.

В процессе исследования излучения нагретых тел было установлено, что любое нагретое тело излучает электромагнитные волны (свет) в широком диапазоне частот.

Тепловое излучение – это излучение электромагнитных волн за счет внутренней энергии тела.

Тепловое излучение имеет место при любой температуре. Однако при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.

Ведем следующие характеристики излучения:

1. энергетическая светимость R(T) – это энергия W, испускаемая 1 м² поверхности светящегося тела за 1 с.

. [R(T)]=Вт/м².

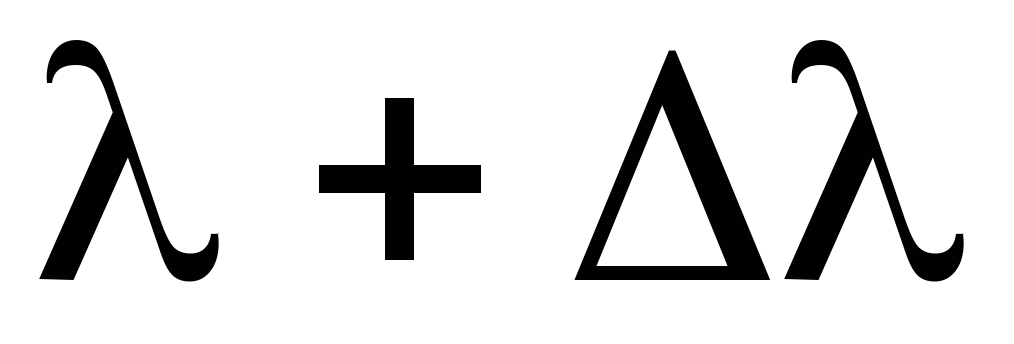2. испускательная способность (спектральная плотность энергетической светимости) r(λ,Т) – это энергия излучения с длинами волн от λ до, испускаемая 1 м² поверхности светящегося тела за 1 с.

. .

.

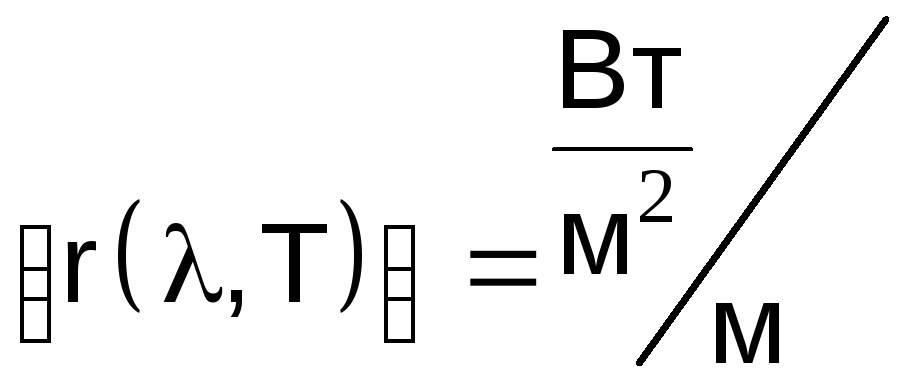3. поглощательная способность тела а(λ,Т) – это отношение энергии с длинами волн от λ до, поглощаемой телом, к энергиис длинами волн от λ до, падающей на поверхность тела.

4.2

Закон Кирхгофа: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией длины волны (частоты) и температуры:

.

Тело, которое при любой температуре полностью поглощает все падающее на него излучение, называется абсолютно черным телом а.ч.т. У абсолютно черного тела поглощательная способность а(λ,Т) = 1. Следовательно, универсальная функция Кирхгофа – это испускательная способность абсолютно черного тела.

Применяя методы термодинамики австрийский физик Йозеф Стефан (1835 – 1893) и австрийский физик-теоретик Людвиг Больцман (1844-1906) в 1879 году частично решили задачу излучения а.ч.т., получив формулу для определения энергетической светимости R_ачт(T). Согласно закону Стефана-Больцмана

, .

В1896-м году группа немецких физиков во главе с другом Макса Планка ВильгельмомВином создали суперсовременную по тем временам экспериментальную установку для исследования распределения интенсивности излучения по длинам волн (частотам) в спектре теплового излучения абсолютно черного тела. Эксперименты, выполненные на этой установке, подтвердили результат, полученный австрийскими физиками Й.Стефаном и Л.Больцманом. Полученные графики распределения интенсивности теплового излучения по частотам были удивительно похожи на полученные ранее Дж. Максвеллом кривые распределения молекул газа, находящегося в закрытом объеме, по величинам скоростей. Из анализа полученных графиков следовало, что с ростом температуры максимум интенсивности смещается в сторону более коротких волн.

Теоретическое объяснение полученных графиков стало центральной проблемой в конце 90-х годов 19-го века.

4.3.

Английские классические физики лорд Рэлей (1842-1919) и сэр Джеймс Джинс (1877-1946) применили к тепловому излучению методы статистической физики (воспользовались классическим законом о равнораспределении энергии по степеням свободы). Рэлей и Джинс применили метод статистической физики к волнам подобно тому, как Максвелл применил его к равновесному ансамблю хаотически движущихся в замкнутой полости частиц. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия равная kT (на электрическую энергию ина магнитную энергию), и получили следующую формулу:

.

Эта формула хорошо описывала ход экспериментальной зависимости при больших длинах волн (низких частотах), но его сравнение с опытными данными, соответствующими малым длинам волн (высоким частотам), вызвало у исследователей настоящий шок. Классическая теория предсказывала бесконечный рост интенсивности излучения в ультрафиолетовой области спектра. Этот эффект получил название ультрафиолетовой катастрофы. Рэлей и Джинс предположили, что стоячей электромагнитной волне любой частоты соответствует одна и та же энергия, и при этом упустили из вида, что при повышении температуры вклад в излучение дают все более и более высокие частоты. Естественно, что принятая ими модель должна была привести к бесконечному росту энергии излучения на высоких частотах. Ультрафиолетовая катастрофа стала серьезным парадоксом классической физики.

Вину с помощью методов термодинамики и электродинамики удалось вывести соотношение, графическое изображение которого удовлетворительно совпадало с коротковолновой (высокочастотной) частью полученных в эксперименте данных, но абсолютно расходилось с результатами опытов для больших длин волн (низких частот).

.

Из этой формулы было получено соотношение, связывающее ту длину волны , которой соответствует максимум интенсивности излучения, и абсолютную температуру тела Т (закон смещения Вина):

, .

Но формулы, описывающей всю кривую, не было.

За решение возникшей проблемы взялся Макс Планк (1858-1947), который в это время работал в департаменте физики в Берлинском институте Кайзера Вильгельма. Планк был очень консервативным членом Прусской Академии, всецело поглощенным методами классической физики. Он был страстно увлечен термодинамикой. Практически, начиная с момента защиты диссертации в 1879-м году, и почти до конца века целые двадцать лет подряд Планк занимался изучением проблем, связанных с законами термодинамики. Планк понимал, что классическая электродинамика не может дать ответа на вопрос о том, как распределена энергия равновесного излучения по частотам. Возникшая проблема относилась к сфере термодинамики. Планк исследовал необратимый процесс установления равновесия между веществом и излучением (светом). Чтобы добиться согласования теории с опытом, Планк отступил от классической теории лишь в одном пункте: он принял гипотезу о том, что излучение света происходит порциями (квантами). Принятая Планком гипотеза позволила получить для теплового излучения такое распределение энергии по спектру, которое соответствовало эксперименту.

.