§1. Эллипс, каноническое уравнение

Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Пусть М - произвольная точка эллипса, F₁, F₂ - его фокусы, расстояние F₁F₂=2 назовем фокальным расстоянием, отрезки F₁M и F₂M назовем фокальными радиусами точки М. Пусть дано постоянное число 2 >2 ( > ), тогда, согласно определению эллипса, имеем:

F₁M + F₂M = 2a. (1)

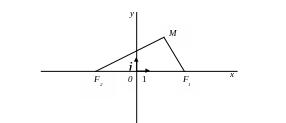
Рис.3. М-точка эллипса, F_1, F₂ – фокусы.

Найдем уравнение эллипса в прямоугольной системе координат O , где О - середина отрезка F₁F₂, ↑↑OF₁ (рис.3). В выбранной системе координат можно указать координаты точек F₁( , ), F₂(- , ). Если М(х,у) - переменная точка эллипса, то F₁M= , F₂M= . Равенство (1) примет вид:

. (2)

Возведя последнее уравнение дважды в квадрат и выполнив алгебраические преобразования, получим:

( ²- ²) ²+ ^{2 2}= ²( ²- ²).

Так как > , то ²- ²>0. Обозначив ²- ² через ², последнее уравнение запишем в виде

+ =1. (3)

Итак, доказано, что координаты любой точки эллипса удовлетворяют уравнению (3).

Так как в ходе преобразований уравнения (2) дважды выполнялось действие возведения уравнения в квадрат, то возможно нарушение равносильности уравнений (2) и (3). Поэтому надо доказать обратное утверждение: если координаты некоторой точки удовлетворяют уравнению (3), то эта точка принадлежит эллипсу, т.е. для нее F₁M+F₂M=2 .

Из уравнения (3) найдем у²=b²(1- ).

Учитывая, что

а² - с² = b² , (4)

найдем:

F₁M= = . (5)

Аналогично получим F₂M= .

Из уравнения (3) следует, что |х|≤а, и так как 0< <1, то а- х>0 и а+ х>0, поэтому F₁M=а- и F₂M=а + .

Следовательно, F₁М+F₂M=2a, т. е. М(х,у) - точка эллипса.

Итак, уравнение (3) является уравнением эллипса. Оно называется каноническим уравнением эллипса и так как это уравнение имеет вторую степень, то эллипс является линией второго порядка.

Замечание. Если фокусы F₁ и F₂ совпадают, то с=0, поэтому из формулы (4) следует, что a=b, и уравнение (3) примет вид: x²+y²=a². Этим уравнением определяется окружность с центром в начале координат и радиусом, равным a. Таким образом, окружность является частным случаем эллипса.

§2. Исследование свойств эллипса

Исследуем геометрические свойства эллипса, заданного в прямоугольной системе координат каноническим уравнением

+ =1. (1)

1. Так как координаты точки О(о,о) не удовлетворяют уравнению (1),

то эллипс не проходит через начало координат.

2. Переменные х и у входят в уравнение (1) в четной степени, поэтому,

если точка М(х,у) принадлежит эллипсу, то эллипсу (1) принадлежат

и точки М₁(-х, у), М₂(х,-у), М₃(-х ,-у). Следовательно, оси Oх и Oу

являются осями симметрии эллипса, а точка О - центром симметрии

или центром эллипса. Ось, на которой лежат фокусы, называется

фокальной осью.

3. Точки пересечения эллипса с осями координат имеют координаты:

А₁(a,0), А₂(-a,0), В₁(0,b), В₂(0,-b). Эти точки называются вершинами

эллипса. Из формулы (4) §1 следует, что a>b при с 0, поэтому

отрезки А₁А₂ и В₁В₂ называются соответственно большой и малой

осями эллипса, а отрезки ОА₁=ОА₂=a и ОВ₁=ОВ₂=b большими и

малыми полуосями соответственно.

4. Из уравнения (1) следует, что |х|≤a, |у|≤b. Геометрически это

означает, что все точки эллипса расположены внутри

прямоугольника, сторонами которого являются прямые х=a, х=-a,

у=b, у=-b, и который называется характеристическим.

5. Чтобы получить представление о форме эллипса, достаточно исследовать поведение его точек, лежащих в первой координатной четверти, и воспользоваться свойством симметричности эллипса относительно осей. Для точки М(х,у), принадлежащей первой четверти, х≥0, у≥0, поэтому из уравнения (1) найдем : у = .

Отсюда видно, что при возрастании х от 0 до a ордината у переменной точки М убывает от b до 0.

На основании рассмотренных свойств изобразим эллипс, заданный формулой (1) (рис.4).

у

В₁

b

P Q

EMBED Equation.DSMT4

А₁ х

0

А₂

-a

a

-b

В₂

S R

Рис.4.Эллипс + =1, PQRS- Характеристический прямоугольник эллипса.