§36. Прямолинейные образующие поверхностей второго порядка

Прямая, все точки которой лежат на поверхности, называется прямолинейной образующей этой поверхности.

Значит, образующие всех цилиндрических и конических поверхностей являются их прямолинейными образующими.

Прямолинейных образующих нет у эллипсоида, двуполостного гиперболоида и эллиптического параболоида из-за следующих их особенностей: эллипсоид - ограниченная поверхность, все его точки лежат внутри параллелепипеда; двуполостный гиперболоид - поверхность, распадающаяся на две части; эллиптический параболоид - поверхность, лежащая по одну сторону от плоскости, проходящей через его вершину.

Докажем, что однополостный гиперболоид и гиперболический параболоид имеют прямолинейные образующие.

1. Запишем уравнение однополостного гиперболоида

(1)

в виде:

(2)

Рассмотрим две системы уравнений:

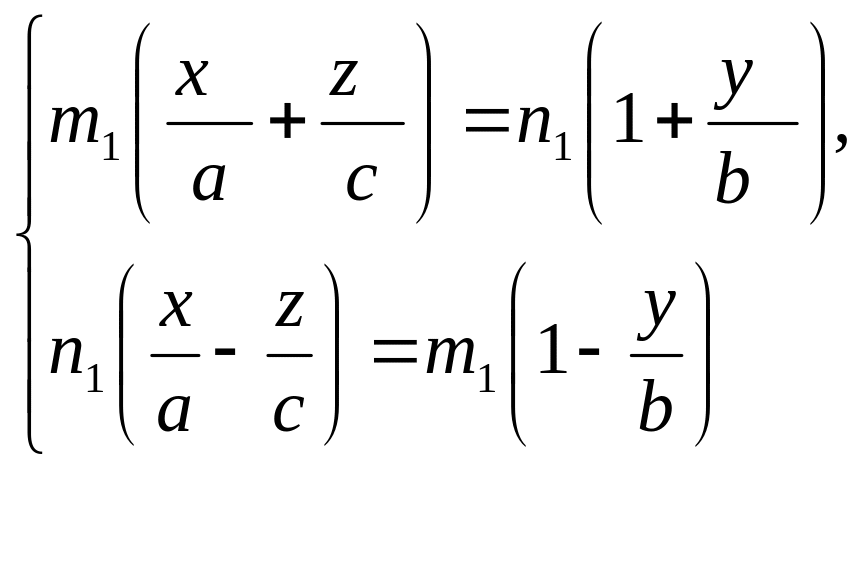(A) и (B)

где - какие-либо действительные числа, из которых хотя бы одно отлично от нуля; этому же условию удовлетворяют числа . Поэтому каждое из уравнений в системах (A) и (B) определяет плоскость при заданных m₁ и n₁, m₂ и n₂.

В каждой из систем (A) или (B) в уравнениях плоскостей коэффициенты при переменных не пропорциональны, поэтому каждая из систем задаёт прямую линию при конкретных значениях и . Если обе части любого уравнения систем (A) и (B) умножить на какое-либо число, то получится уравнение, равносильное первоначальному. Поэтому для определения направления прямых (A) и (B) играют роль не сами числа и , а лишь их отношения и .

Если точка удовлетворяет системам уравнений (A) и (B), то она удовлетворяет и уравнению (1). Это означает, что каждая прямая, определяемая системой (A) или (B), лежит на данной поверхности, т.е. является её прямолинейной образующей.

Прямые, определяемые системой (A) при всевозможных значениях , не равных нулю одновременно, образуют одно семейство прямолинейных образующих однополостного гиперболоида (1), а прямые, определяемые системой (B) при различных значениях , не равных нулю одновременно, - другое семейство прямолинейных образующих этой поверхности.

Можно доказать, что прямолинейные образующие однополостного гиперболоида обладают следующими свойствами:

1) Через каждую точку однополостного гиперболоида проходит две и только две прямые, принадлежащие разным семействам: одна из них принадлежит семейству (A), а другая - семейству (B).

2) Любые две прямолинейные образующие одного семейства скрещиваются.

3) Любые две прямолинейные образующие из разных семейств лежат в одной плоскости, но не совпадают.

Схематичный чертёж однополостного гиперболоида с двумя семействами прямолинейных образующих дан на рис.57.

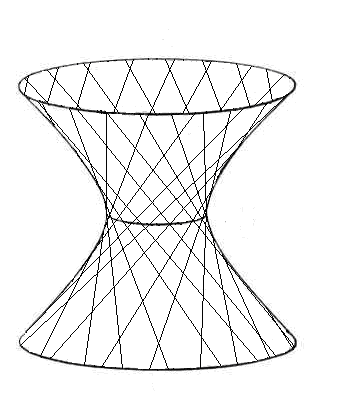
Рис.57.Прямолинейные образующие однополостного гиперболоида.

Известный инженер Владимир Григорьевич Шухов (1853-1939) предложил устройство мачт, башен, опор, составленных из балок, расположенных по прямолинейным образующим однополостного гиперболоида вращения. Эти конструкции В.Г. Шухова оказались очень прочными и легкими. Они очень часто используются при строительстве водонапорных башен, высотных радиомачт, телемачт.

2. Уравнение гиперболического параболоида

(3)

можно представить в виде:

Рассмотрим две системы:

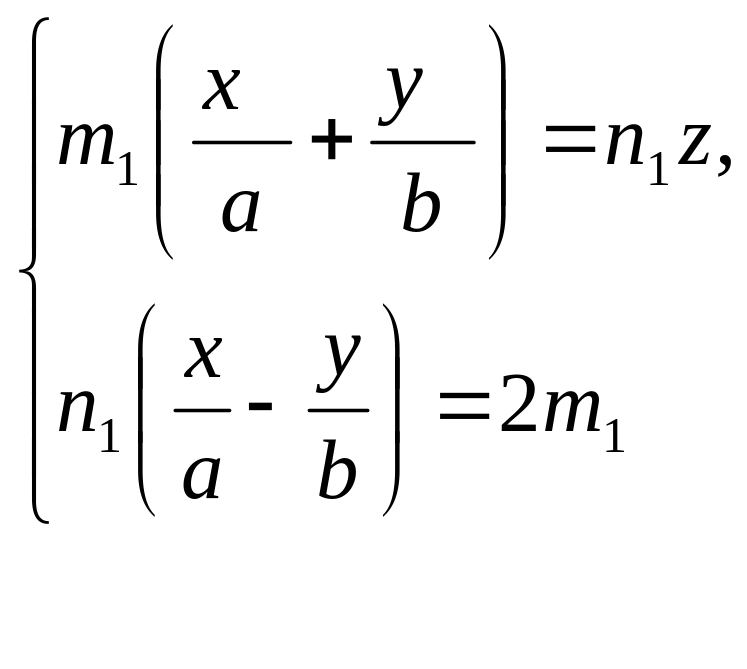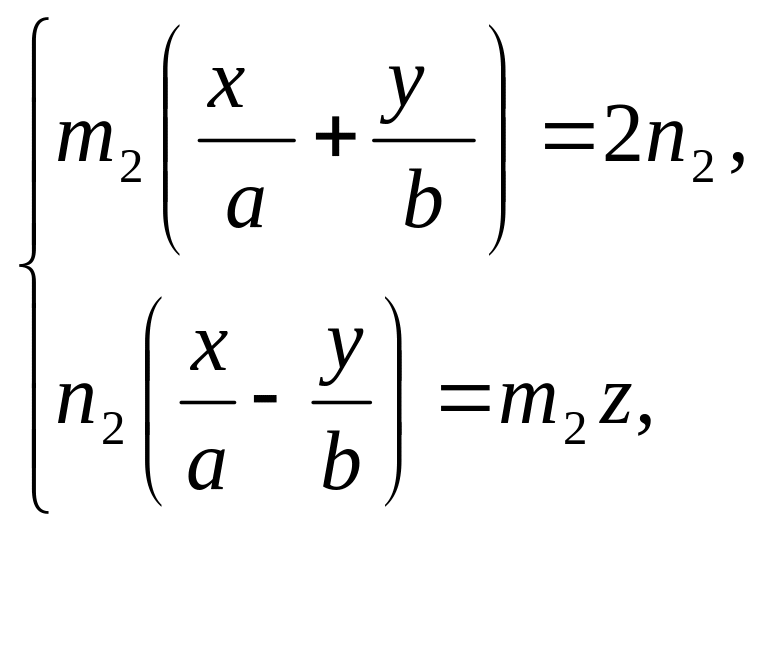(A) и (B)

где в парах действительных чисел и хотя бы одно из чисел пары не равно нулю.

Далее, рассуждая так же, как в п.1, можно показать, что системы (A) и (B) определяют два семейства прямолинейных образующих гиперболического параболоида.

Прямолинейные образующие гиперболического параболоида обладают теми же свойствами 1), 2), 3), что и образующие однополостного гиперболоида, и ещё свойством

4) Все прямолинейные образующие семейства (A) параллельны плоскости , а все прямолинейные образующие семейства (B) параллельны плоскости .

Гиперболический параболоид с двумя семействами прямолинейных образующих дан на рис.58.

Рис.58. Прямолинейные образующие гиперболического параболоида.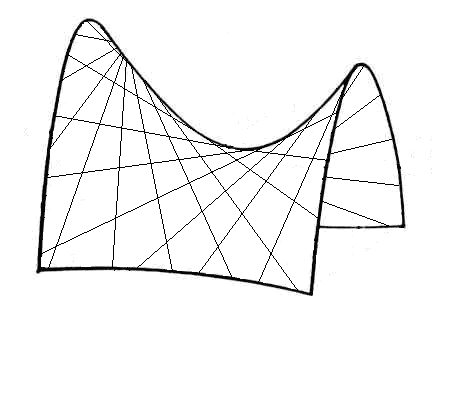

Пример. Найти прямолинейные образующие гиперболического параболоида

проходящие через его точку .

Решение. Запишем уравнения двух семейств прямолинейных образующих заданного параболоида.

(A) и (B)

Так как точка принадлежит прямолинейным образующим, то подставив координаты точки в системы (A) и (B), получим:

Из первой системы получаем, что Например, если , тогда Из второй системы получаем, что Можно взять , тогда . Подставив полученные значения в систему (A), а значения - в систему (B), получим две прямолинейные образующие заданной поверхности, проходящие через точку :

и