§33. Двуполостный гиперболоид

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

(формула 15°§25) (1)

По каноническому уравнению (1) можно исследовать простейшие свойства этой поверхности.

1. Точка О(0,0,0) не принадлежит поверхности (1).

2. Оси координат, координатные плоскости и начало координат являются соответственно осями симметрии, плоскостями симметрии и центром симметрии конуса (1).

3. Точки пересечения с осью Oz: (0,0, c).

Действительных точек пересечения с осями Ox и Oy нет.

Поэтому ось Oz называется действительной осью, а оси Ox и Oy - мнимыми осями поверхности.

Точки (0,0,c) и (0,0,-c) назовём вершинами двуполостного гиперболоида.

4. Если поверхность (1) пересечь плоскостью z = h, то проекция сечения на плоскость Oxy имеет уравнение:

(2)

Возможны случаи:

а) Если , то сечения, определяемые формулой (2), будут представлять собой действительные эллипсы.

б) Если , то секущая плоскость z=h действительных точек пересечения с поверхностью (1) не имеет.

в) Если или , то каждая из секущих плоскостей z=c и z=-c имеет с поверхностью (1) одну общую точку (0,0,с) и (0,0,-с) соответственно.

Если пересекать поверхность (1) плоскостями x=h или y=h, то в сечениях в обоих случаях при любых h получаются гиперболы.

Так как действительные точки двуполостного гиперболоида существуют лишь при и , то эта поверхность распадается на две части.

Исследовав вопрос о пересечении двуполостного гиперболоида с прямыми, проходящими через начало координат аналогично тому, как это делалось для однополостного гиперболоида в предыдущем параграфе, получим тот же асимптотический конус, что и для однополостного гиперболоида. Однако, в отличие от однополостного гиперболоида, все точки двуполостного гиперболоида лежат внутри асимптотического конуса.

Изображение двуполостного гиперболоида имеет вид:

x

y

z

c

-c

0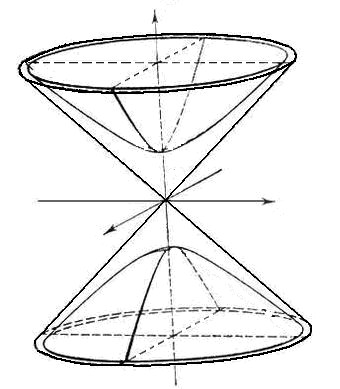

Рис.54. Двуполостный гиперболоид.

Если в уравнении (1) a=b, то уравнение поверхности принимает вид:

.

Эта поверхность называется двуполостным гиперболоидом вращения с осью вращения Oz.

Любой двуполостный гиперболоид можно получить из двуполостного гиперболоида вращения с помощью сжатия к плоскости, проходящей через ось вращения.

§34. Эллиптический параболоид

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

(формула 16°§25) (1)

Из канонического уравнения (1) следуют свойства этой поверхности.

1. Точка O(0,0,0) принадлежит поверхности.

2. Так как x и y входят в уравнение (1) в четных степенях, а z - в нечетной степени, то эллиптическому параболоиду принадлежат одновременно точки: (x,y,z), (-x,y,z), (x,-y,z) и (-x,-y,z). Это означает, что поверхность (1) симметрична относительно плоскостей Oyz, Oxz и оси Oz, которую назовём осью поверхности. Симметрий относительно плоскости Oxy, осей Ox, Oy и начала координат нет.

3. Точка О(0,0,0) является точкой пересечения поверхности со всеми осями координат и называется вершиной поверхности.

4. Из уравнения (1) следует, что для всех точек поверхности , причём, лишь для вершины поверхности. Значит, все точки поверхности, кроме вершины, лежат по одну сторону от плоскости Oxy.

Изучая форму поверхности методом сечений, получим:

1) В сечении поверхности (1) плоскостью z=h получается линия, равная следующей проекции сечения на плоскость Oxy:

(2)

Уравнение (2) определяет либо действительный эллипс при h>0, либо вершину поверхности при h=0, либо мнимый эллипс при h<0. С возрастанием h 1° неограниченно возрастают полуоси эллипса (2).

2) В сечении поверхности (1) плоскостью y=h получается линия, равная проекции сечения на плоскость Oxz:

(3)

Уравнение (3) определяет множество парабол, равных между собой и равных параболе , получающейся в сечении поверхности плоскостью Oxz.

3) Аналогично убеждаемся, что в сечении поверхности (1) плоскостью x=h получается парабола. При различных h получаются параболы, равные параболе , лежащей в плоскости Oyz.

Эллиптический параболоид изображён на следующем рисунке.