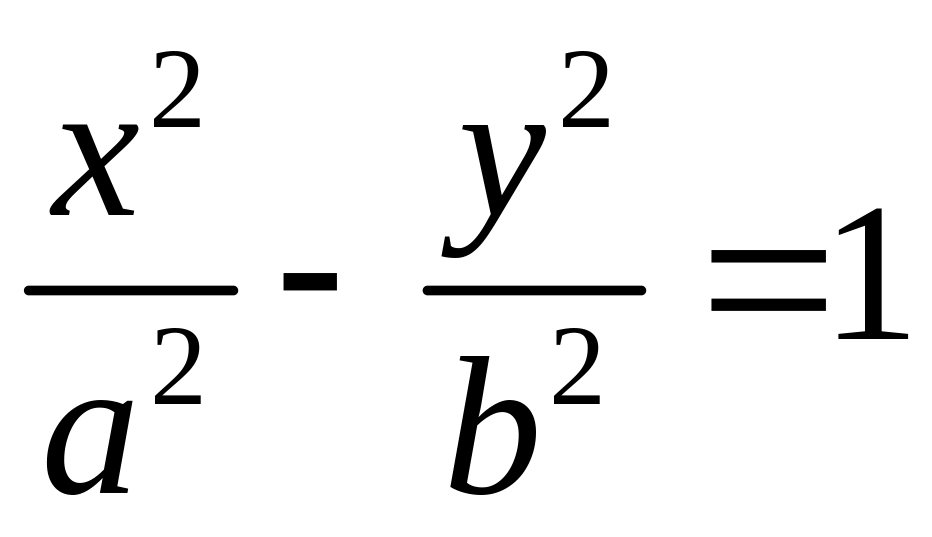§ 29. Цилиндры второго порядка

Если уравнение направляющей линии : F(x,y)=0 является уравнением второй степени, т.е. является линией второго порядка, то цилиндрическая поверхность с направляющей линией является цилиндрической поверхностью второго порядка (кратко: цилиндром второго порядка). Так как существует 9 классов линий второго порядка, то существует и 9 классов цилиндров второго порядка. Схематичные рисунки цилиндров второго порядка, заданных каноническими уравнениями, представлены в следующей таблице.

Таблица 3.

№	Каноническое уравнение	Название поверхности	Поверхность
		Эллиптический цилиндр	z x y
		Мнимый эллиптический цилиндр	Действительных точек нет
		Вырожденный эллиптический цилиндр (прямая)	z z
		Гиперболический цилиндр	x y
		Две пересекающиеся плоскости	z x
	,	Параболический цилиндр	z x y
	,	Две параллельные плоскости	z
	,	Две мнимые параллельные плоскости	Действительных точек нет
		Две совпадающие плоскости	x y

Если в уравнении 1° =b, то направляющей эллиптического цилиндра будет окружность х²+ у²= ². В этом случае поверхность будет круговым цилиндром. Её можно получить вращением любой образующей вокруг оси Oz.

Получили поверхности - указанные в §25. Особенность цилиндрических поверхностей заключается в том, что если эллиптический, гиперболический или параболический цилиндры пересекать различными плоскостями, не параллельными образующим, и не обязательно перпендикулярно образующим, то во всех сечениях этих цилиндров будут получаться соответственно эллипсы, гиперболы и параболы.

§ 30. Коническая поверхность второго порядка

П

M

М'

M₀

усть в пространстве дана линия и точка М₀ . Коническую поверхность можно образовать всеми прямыми, проходящими через точку M₀ и через каждую точку М' линии . Точка М₀ называется вершиной конуса, линия называется направляющей, а прямые М₀М - образующими конической поверхности. Видим, что вместе с каждой своей точкой М поверхность содержит и всю прямую М₀М.

К

Рис.47. Коническая поверхность

онической поверхностью или конусом с вершиной в точке M₀ называется поверхность,

которая обладает тем свойством, что вместе с каждой

своей точкой М, отличной от точки М₀, эта

поверхность содержит прямую М₀М.

Рассмотрим частный случай конуса, вершина которого совпадает с началом системы координат, а направляющей служит линия второго порядка, лежащая в плоскости, параллельной какой-нибудь координатной плоскости. Пусть направляющей служит эллипс, заданный уравнениями

. (1)

Этот эллипс лежит в плоскости, параллельной координатной плоскости Oxy.

Составим уравнение конуса с вершиной в точке О(0,0,0). Возьмем точку M(x,y,z) конуса, отличную от точки О. Прямая ОМ пересечет направляющую в точке . Векторы и коллинеарны, поэтому существует такое число t, что или в координатах: х'= tx, = ty, с= tz. Из уравнения (1)следует, что z 0, поэтому находим: , , .

z=c

x

O

z

y

M

Точка М' , поэтому полученные значения и подставим в уравнение(1) линии и после преобразований найдем уравнение:

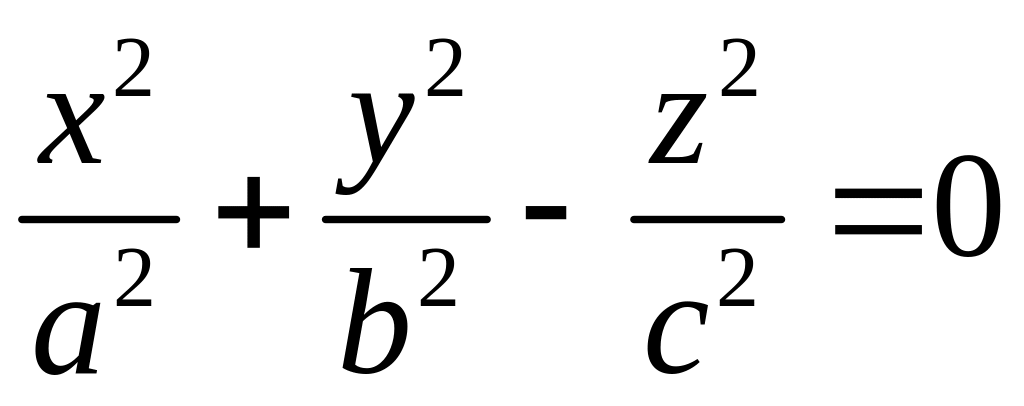. (2)

Э тому уравнению удовлетворяют и координаты точки (0,0,0) - вершины конуса. Таким образом, координаты любой точки конуса удовлетворяют уравнению (2). Несложно доказать, что если точка N не принадлежит конусу, то её координаты не удовлетворяют уравнению (2).

Рис.48. Коническая поверхность с вершиной в начале системы координат

Итак, уравнение (2) является уравнением конуса. Так как уравнение (2) имеет степень, равную 2, то такой конус называется конусом второго порядка. Уравнение (2) назовем каноническим уравнение конуса, оно совпадает с уравнением 10° §25.

Так как переменные x, y, z входят в уравнение (2) в четных степенях, то конус (2) симметричен относительно всех координатных осей, координатных плоскостей и начала координат. Одну из осей симметрии, а именно, ось Oz, назовем осью конуса (2).

Уравнению (формула 11° §25) удовлетворяет своими координатами единственная точка O(0,0,0). Такую поверхность назовем мнимым конусом с вершиной в точке О.

Если направляющей конуса служит окружность, т.е. в уравнение (2) =b, то такой конус называется круговым. Его можно получить вращением любой образующей вокруг оси Oz.

Уравнения и также определяют конусы с осями Oy и Ox соответственно.

Если вершина конуса М₀ - произвольная точка пространства и линия - произвольная линия пространства (общий случай конуса), то уравнение такого конуса можно найти из условия, вытекающего из определения конуса:

= ,

где М - переменная точка конуса, - переменная точка направляющей конуса, t - параметр.

В отличие от цилиндрических поверхностей второго порядка конусы второго порядка обладают тем свойством, что в их сечениях можно получить все три линии второго порядка - эллипс, гиперболу и параболу. Это зависит от того, как расположить секущую плоскость П (см. рис. 49, 50, 51).

Р

П

П

П

ис.49. Рис.50. Рис.51.

Секущая плоскость П Секущая плоскость П Секущая плоскость пересекает все параллельна одной П пересекает обе образующие конуса. образующей конуса. полости конуса.