§22. Главные диаметры, оси линии второго порядка

Диаметр линии второго порядка называется главным, если он со­пряжен с перпендикулярным ему направлением.

Теорема 1. Центральная линия 2-го порядка, кроме окружности, имеет два главных диаметра; для окружности любой диаметр является главным; нецентральные линии имеют только один главный диаметр.

Доказательство. 1) Пусть линия 2-го порядка - центральная и отличная от окружности. Тогда она имеет два главных направления. Оба направления неасимптоти­ческие, так как если бы одно из них было асимптотическим, то для цен­тральной ли­нии оно самосопряжено (следствие 2 §20), что привело бы к противоречию. Диаметры, сопряженные хордам двух глав­ных направлений, являются главными диамет­рами.

2) Если линия второго порядка - окружность, то по теореме §21 для неё любое направ­ление является главным. Окружность - это линия эллиптиче­ского типа, она не имеет аси­мптотических направлений и поэтому с каждым направлением будет сопряжен главный диаметр.

3) Пусть линия второго порядка - нецентральная, т.е. параболического типа. Она имеет два главных направления. Можно показать, что одно главное направление совпа­дает с асимптотическим направлением, а значит другое перпендикулярно асимптотиче­скому направлению. По свойству 7) §18 получаем, что все диаметры нецентральной линии параллельны между собой и параллельны вектору асимптотического направления. Диаметр, сопряжен­ный неасимптотическому главному направлению, является единственным главным диа­мет­ром нецентральной линии.

Осью симметрии фигуры называется прямая, относи­тельно кото­рой фигура симметрична.

Теорема 2. Главные диаметры линии второго порядка являются её осями симмет­рии.

Доказательство. Любой диаметр, сопряженный вектору неасимптоти­ческого на­правления, проходит через середины хорд, параллельных вектору . Так как главный диа­метр перпендикулярен вектору , то он перпендикулярен и хордам, а поэтому является осью симметрии, что доказывает теорему 2.

Из теоремы 1 следует, что любая линия второго порядка имеет хотя бы одну ось симметрии. Эллипс с неравными полуосями и гипербола имеют две оси симметрии, ок­ружность - бесконечное множество, парабола - только одну. Кроме главных диаметров у некоторых линий есть и другие оси. У параллельных прямых х²-а²=0 осями являются главный диаметр и все прямые, перпендикулярные этим прямым. Линия х²-у²=0, распадающаяся на пару перпендикулярных прямых, имеет 4 оси симметрии: два главных диаметра и сами эти прямые.

§23. Получение канонических уравнений линий второго порядка при помощи ортогональных инвариантов

Пусть линия второго порядка задана в прямоугольной системе коорди­нат общим уравнением

a₁₁x² + 2a₁₂xy + a₂₂y² + 2a₁₀x + 2a₂₀y + a₀₀ = 0. (1)

Так как левая часть этого уравнения является квадратичной функцией, то ортогональные инварианты квадратичной функции являются ортогональными инвариантами линии вто­рого порядка, заданной уравнением (1), т.е. это числа:

, , .

В §§12 и 13 было доказано, что при помощи поворота системы координат Oxy на угол α вокруг начала координат и параллельного переноса можно получить новую систему координат , в которой уравнение (1) приводится к одному из следующих уравнений:

A + B + C=0, где A≠0, B≠0; ( I )

A + B =0, где A≠0, B≠0; ( II )

A + C=0, где A≠0. ( III )

Будем говорить, что линия второго порядка относится к группе I, II или III соответст­венно тому, сводится ли уравнение (1) к уравнению (I), (II) или (III).

С помощью инвариантов I₁, I₂, I₃, I₄ (§11) можно найти значения коэффициентов в урав­нениях (I), (II), (III).

Теорема 1. Для того, чтобы линия второго порядка, заданная в прямоугольной сис­теме координат общим уравнением (1), относилась к группе I, необходимо и достаточно, чтобы I₂≠0; к группе II - I₂=0, I₃≠0; к группе III - I₂=0, I₃=0, I₁≠0.

Доказательство необходимости. 1) Пусть линия второго порядка принадлежит группе I , значит, она определяется уравне­нием (I). Найдем инвариант I₂.

. Так как A ≠ 0, B ≠ 0, то I₂ ≠ 0.

Причем, если линия относится к эллиптическому типу, то коэффициенты A и B будут одного знака, значит, I₂>0; если линия относится к гиперболическому типу, то коэффициенты A и B разных знаков, поэтому I₂<0.

2) Пусть уравнение (1) приводится к виду (II), т.е. относится к группе II. В этом случае

, .

3) Пусть линия (1) относится к группе III, тогда

, , I₁=A 0.

Доказательство достаточности можно получить методом от противного.

Пусть I₂≠0. Докажем, что линия (1) принадлежит группе I. Допустим противное, что эта линия принадлежит группе II или группе III. Тогда в силу необходимости I₂=0, что приводит к противоречию.

Аналогично доказывается, что если I₂=0, I₃≠0, то линия принадлежит группе II , а если I₂=0, I₃=0, I₁≠0 - то группе III .

Теорема 2. Если линия второго порядка задана общим уравнением (1) относительно прямоугольной системы координат, то ее про­стейшие уравнения имеют вид:

λ₁ +λ₂ +I₃/I₂=0, (2)

λ₁ ± 2 =0, если λ₁≠0 (λ₂ ± 2 =0, если λ₂≠0), (3)

λ₁ +I₄/I₁=0, λ₁≠0 (λ₂ +I₄/I₁=0, λ₂≠0), (4)

соответственно тому, является ли эта линия линией I, II или III группы, причем, в формулах (2), (3), (4) λ₁ и λ₂ - корни характеристического уравнения

λ²-I₁λ+I₂=0. (5)

Доказательство. 1) Пусть линия, заданная уравнением (1), относится к группе I. Тогда по уравнению (I) найдем инварианты: I₂=А·В, I₁=А+В. По теореме Виета из урав­нения (5) следует, что А и В являются корнями этого уравнения. Пусть А=λ₁, В=λ₂.

Найдем . Отсюда С=I₃/I₂. Значит, уравнение (I) имеет вид (2).

2) Пусть линия (1) относится к группе II . Из уравнения (II) найдем

. Отсюда В=± 2 .

Так как для группы II инвариант I₂=0, то характеристическое уравнение этой линии имеет вид:

λ² - Аλ=0.

Пусть λ₁=А, λ₂=0. Тогда уравнение (II) имеет вид (3).

3) Пусть, наконец, линия (1) принадлежит к группе III. Тогда из уравнения (III) находим:

I₁=А, I₂=0, I₃=0.

Характеристическое уравнение примет вид:

λ² - Аλ=0.

Пусть λ₁=А, λ₂=0.

Из теоремы 2 §11 следует, что для линии группы III ортогональным инвариантом явля­ется инвариант .

Имеем: . Отсюда С=I₄/I₁.

Значит, уравнение (III) примет вид (4).

Теорема 3 (без доказательства). Необходимыми и достаточными условиями (признаками) каждого из девяти классов линий второго порядка являются условия, указанные в следующей таблице.

Таблица 2.

№	Название линии	Признаки
1	Эллипс	I2>0	I1∙I3<0
2	Мнимый эллипс		I1∙I3>0
3	Вырожденный эллипс (точка)		I3=0
4	Гипербола	I2<0	I3≠0
5	Две пересекающиеся прямые		I3=0
6	Парабола	I2=0	I3≠0
7	Две действительные параллельные прямые		I3=0	I4<0
8	Две мнимые параллельные прямые			I4>0
9	Две совпадающие прямые			I4=0

Имея уравнение линии второго порядка в виде (2), (3) или (4), несложно перейти к ка­ноническому уравнению этой линии.

Если линия (1) приведена к од­ному из уравнений (2), (3) или (4), то для опре­деле­ния её расположения относительно системы координат, достаточно знать пара­метры, ха­ракте­ризующие данную линию, и ту сис­тему координат, в которой уравнение линии явля­ется каноническим.

Направление осей новой системы координат определяется так, как это было указано в §21 при а₁₂≠0 и а₁₂=0 .

Если линия (1) является цен­тральной линией (I₂≠0), то надо найти полуоси линии и её центр.

Если уравнение (1) определяет параболу (I₂=0), то надо найти её па­раметр, глав­ный диаметр, который имеет асимптотическое направление, вершину и направление по­луоси, на которой лежит фокус.

Если линия (1) распадается на две действительные прямые, то надо найти уравнение главного диаметра, который определит ту ось новой сис­темы координат, относительно кото­рой можно построить линию по её ка­ноническому уравнению.

Примеры. С помощью инвариантов привести уравнения заданных линий к каноническому виду и построить эти линии.

Пример 1. 2ху + 4х + 2у + 5 = 0 (6)

Найдем инварианты: I₁=0, I₂=-1, I₃=-1. Так как I₂<0, I₃≠0, то данное уравнение определяет гиперболу.

Составим характеристическое уравнение: λ² - 1=0. Отсюда λ₁=1, λ₂=-1.

Используя формулу (2), получим уравнение: - + =0, т.е. уравнение:

- =-1.

Найдем центр гиперболы по формулам a₁₁x+a₁₂y+a₁₀=0,

a₂₁x+a₂₂y+a₂₀=0,

т .е. из системы: y + 2 = 0, x=-1, y=-2.

x + 1 = 0.

Таким образом, точка (-1; -2) является центром гиперболы.

Найдем направление оси координат . Так как в уравнении линии а₁₂≠0, то угловой коэффициент т.е. вектор (1,1) определяет направление оси . Угловой коэффициент . Поэтому вектор (1,-1) определяет направление оси .

Построим гиперболу.

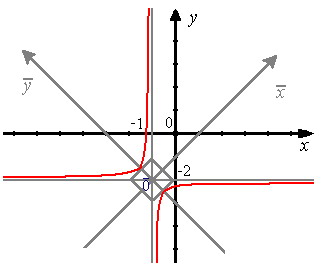
Рис.35. Гипербола, заданная уравнением (6).

Пример 2. (7)

Найдем инварианты:

, ,

, поэтому заданная линия - эллипс.

Характеристическое уравнение имеет корни , .

Каноническое уравнение линии примет вид:

, .

Найдем центр линии:

Т.к. в заданном уравнении коэффициент то векторы определяют направления осей линии.

Построим линию.

Рис.36. Эллипс, заданный уравнением (7).

Пример 3. . (8)

, , ,

Т.к. то данное уравнение определяет две параллельные прямые.

Заданное уравнение линии можно записать в виде:

Рис.37. Параллельные прямые, заданные уравнением (8).

Пример 4. (9)

Найдем инварианты:

Так как а то линия - гипербола.

Составим характеристическое уравнение:

. Отсюда получаем корни

По формуле (2) получим уравнение

или .

Получили уравнение гиперболы с полуосями a=3 и b=1, причем, a - мнимая полуось.

Найдем центр линии из системы уравнений:

Получаем точку С(-1,2), являющуюся центром гиперболы.

Найдем угловые коэффициенты k₁ и k₂ новых осей координат и .

Так как в заданном уравнении коэффициент a₁₂=3 0, то , , т.е. k₁= , k₂=3.

Векторы или и определяют направления осей и соответственно.

П

остроим линию:

A₁

A₂

B₁

B₂

x

у

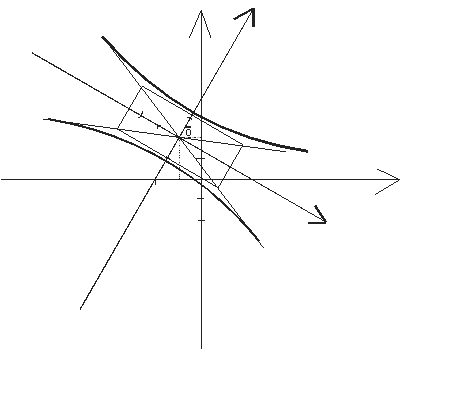
Рис.38.Гипербола, заданная уравнением (9)

Пример 5. (10)

Найдем инварианты линии:

, , . Т.к. , , то данная линия является параболой.

Характеристическое уравнение линии имеет вид: . Его корни , .

Простейшее уравнение линии найдем в виде (3) и получим:

, т.е. .

Каноническое уравнение примет вид: .

Найдем асимптотическое направление параболы из условия: т.е. из равенства . Отсюда , т.е. , следовательно , значит, вектор является вектором асимптотического направления.

Найдем вектор , поэтому определяет направление главного диаметра d параболы:

d: , т.е. прямая является главным диаметром.

Вершину параболы найдем как точку пересечения параболы с главным диаметром:

Отсюда получаем точку , являющуюся вершиной параболы.

Для уточнения расположения параболы относительно осей координат найдем пересечение параболы с осями координат.

Если в заданном уравнении линии положить x=0, то получаем уравнение , которое не имеет действительных корней. Значит, с осью Oy линия не пересекается.

Если в заданном уравнении линии положить y=0, то уравнение имеет корни , , которые являются точками пересечения параболы с осью Ox.

Построим параболу.

Рис.39. Парабола, заданная уравнением (10).

Пример 6.

Найдем инварианты линии: , , .Так как то линия является вырожденным эллипсом - точкой.

Найдем эту точку из системы уравнений, определяющих центр линии:

Таким образом, точка A( ) определяется заданным уравнением

Построим точку:

х

y

A

1

1

-1

-1

-2

Рис.40. Точка, заданная уравнением (11).

Пример 7. (12)

Найдем Т.к. то данное уравнение определяет эллипс. Характеристическое уравнение имеет корни Уравнение эллипса примет вид (2), т.е.

, .

Найдем главные направления.

,

Вычислим центр. - центр линии.

Построим линию.

Рис.41. Эллипс, заданный уравнением (12).

Пример 8. (13)

Найдем По теореме 3 линия является параболой.

Характеристическое уравнение имеет корни

Уравнение параболы примет вид (3): , т.е. Найдем главные направления. Так как в заданном уравнении коэффициент то главные направления определяют векторы и Найдем главный диаметр, соответствующий вектору : Равенство неверно, поэтому диаметра соответствующего направлению не существует.

Для вектора найдем главный диаметр: =0 - главный диаметр, он же является осью параболы. Вершину параболы найдем из системы:

Итак, точка - вершина параболы.

Определим направление ветвей параболы.

Уравнение оси : или . Исследуем расположение точки и точки параболы относительно прямой

Пусть

, Эти точки лежат по одну сторону от

.

прямой

Построим параболу.

Рис.42. Парабола, заданная уравнением (13).