§20. Сопряженные направления

Пусть вектор (р₁,р₂) является вектором неасимптотического направле­ния относи­тельно линии

a₁₁x² + 2a₁₂xy + a₂₂y² + 2a₁₀x + 2a₂₀y + a₀₀ = 0. (1)

Равенство (3) §19 можно записать в виде:

a₁₁ p₁ q₁ + a₁₂ p₁ q₂ + a₂₁ p₂ q₁ + a₂₂ p₂ q₂ = 0. (2)

Направление ненулевого вектора (р₁,р₂) называют сопряженным с направлением ненулевого вектора (q₁,q₂) относительно линии (1), если верно равенство (2).

Так как a₁₂=a₂₁, то понятие сопряженности является взаимным. Поэтому кратко можно говорить, что векторы и сопряжены относительно линии второго порядка, заданной уравнением (1).

Пусть вектор (р₁,р₂) имеет асимптотическое направление, тогда выполняется равенство:

a₁₁ р₁² + 2 a₁₂ р₁р₂ + a₂₂ р₂² = 0.

Запишем его в другом виде:

a₁₁ p₁ p₁ + a₁₂ p₁ p₂ + a₂₁ p₂ p₁ + a₂₂ p₂ p₂ = 0.

Сравнив последнее равенство с равенством (2), можно сделать вывод: каж­дый вектор асимптотического направления самосопряжен.

Теорема. Понятие сопряженности относительно линии второго порядка не зависит от выбора сис­темы координат, а имеет геометрический смысл.

Доказательство. 1) Пусть вектор (р₁,р₂) является вектором неасимптотического направления. Равенство (2) можно записать в виде:

(a₁₁ р₁ + a₁₂ p₂)q₁ + (a₂₁ р₁ + a₂₂ p₂)q₂ = 0. (3)

Направление любого ненулевого вектора , удовлетворяющее этому равенству, как следует из формулы (2) §19, будет совпадать с направлением

д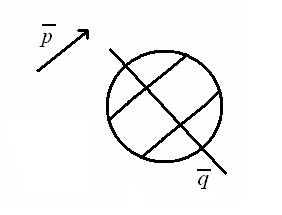 иаметра d, который делит пополам хорды, параллельные вектору (рис.34).

d

Рис.34. Векторы и сопряжены относительно линии второго порядка.

Таким образом, существует только одно направление, сопряженное с вектором , и это направление имеет простой геометрический смысл: оно параллельно диаметру d.

2) Пусть вектор (р₁, р₂) имеет асимптотическое направление и линия (1) централь­ная. Условие (2) опять можно записать в виде (3).

Так как линия (1) центральная, то она не параболического типа, поэтому согласно лемме §16 выражения a₁₁ р₁+a₁₂ p₂ и a₂₁ р₁+a₂₂ p₂ не равны нулю одновременно. Пусть a₂₁ р₁+a₂₂ p₂≠0, тогда в (3) q₁≠0, так как иначе и q₂=0. Разделим обе части равенства (3) на q₁ и, введя угловой коэффициент , получим . ^{Отсюда следует, что угловой коэффициент для вектора} (q₁,q₂) принимает постоянное значение. Значит, векторы, сопряженные вектору , коллинеарны между собой, т.е. существует лишь одно направление, сопряженное вектору . Но вектор имеет асимптотическое направление, поэтому он самосопряжен. Значит, единственным направлением, сопряженным с вектором , будет направление самого вектора .

3) Пусть вектор (р₁, р₂) имеет асимптотическое направление, а линия (1) нецен­тральная. В этом случае линия (1) будет параболического типа, поэтому по лемме §16 вы­полняется условие:

a ₁₁ р₁ + a₁₂ p₂ = 0,

a₂₁ р₁ + a₂₂ p₂ = 0.

^{Равенство (3) примет вид:}

0∙q₁ + 0∙q₂ = 0.

Отсюда следует, что q₁ и q₂ любые действительные числа. Значит, вектор сопряжен с любым вектором. Таким образом, и в этом случае вектор, сопряженный с вектором , не зависит от выбора системы координат, а определяется геометрически.

^{Из доказанной теоремы вытекают следствия.}

^{Следствие 1. Вектор неасимптотического направления сопряжен с вектором не­асимптотического направления.}

^{Следствие 2. Вектор асимптотического направления относительно центральной линии сопряжен лишь сам с собой.}

^{Следствие 3. Вектор асимптотического направления относительно нецентральной линии сопря­жен с любым другим вектором.}