§18. Диаметры линий второго порядка
Пусть линия второго порядка задана общим уравнением
. (1)
Возьмем вектор
неасимптотического направления
относительно этой линии и рассмотрим
множество середин хорд, параллельных
вектору
.
Теорема. Множество середин хорд линии (1), параллельных вектору неасимптотического направления, есть прямая, определяемая уравнением
.
(2)
Доказательство. Пусть - середина какой-либо хорды. По лемме §17 можно записать условие, которому удовлетворяют координаты середины хорды. Это условие примет вид (2). Докажем, что уравнение (2) является уравнением первой степени, то есть определяет прямую линию. Запишем его в виде:
. (3)
Так как вектор имеет неасимптотическое направление, то
или иначе
.
Отсюда следует,
что коэффициенты при
и
в уравнении (3) не равны нулю одновременно,
поэтому уравнение (3), а, значит, и уравнение
(2) определяют прямую линию. Эту прямую
называют диаметром, сопряженным хордам
данного направления, или сопряженным
вектору
.
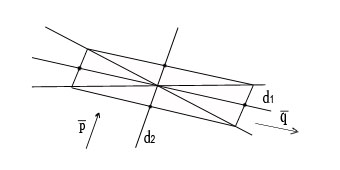
Диаметром линии второго порядка, сопряженным вектору неасимптотического направления, называется множество середин хорд, параллельных этому вектору (рис.29).
d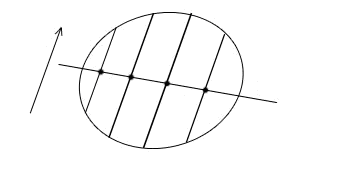
Рис.29. Диаметр d, сопряженным вектору .
Рассмотрим некоторые свойства диаметров.
1) Если линия второго
порядка имеет центры, то каждый диаметр
проходит через каждый центр. Действительно,
если точка
- центр линии второго порядка, то
и
,
поэтому координаты
удовлетворяют уравнению (2) любого
диаметра.
2) Из свойства 1) следует, что если линия второго порядка имеет более одного центра, то она имеет единственный диаметр.
3) Диаметром линии эллиптического типа является любая прямая, проходящая через ее центр.
4) Диаметром линии гиперболического типа является любая прямая, проходящая через центр и отличная от асимптот.
5) Диаметры линии параболического типа имеют асимптотическое направление.
Пусть
- диаметр линии параболического типа.
Уравнение этого диаметра запишем в виде
(3). Тогда его направляющим вектором
будет вектор
.
Согласно лемме §16 координаты вектора
,
имеющего асимптотическое направление,
должны удовлетворять системе
С помощью подстановки убеждаемся, что вектор удовлетворяет этим условиям.
6) Из свойства 5) следует, что все диаметры параболы параллельны оси параболы.
7) Любые два диаметра нецентральной линии параллельны.
§19. Сопряженные диаметры
Пусть в аффинной системе координат центральная линия второго порядка задана общим уравнением
(1)
и пусть вектор
имеет неасимптотическое направление
относительно этой линии. Значит, каждая
прямая, параллельная вектору
,пересекает
линию
в двух точках. Множество середин
полученных хорд образует диаметр
,
сопряженный с вектором
.
Пусть
- направляющий вектор диаметра
.
Может случиться, что диаметр
сам имеет неасимптотическое направление.
Тогда каждая прямая, параллельная
диаметру
,
пересекает линию
в двух точках. Множество середин хорд,
полученных таким образом, образует
другой диаметр
,
сопряженный с вектором
.
Теорема.
Если диаметр
центральной линии второго порядка делит
пополам хорды, параллельные вектору
,
а диаметр
делит пополам хорды, параллельные
диаметру
,
то диаметр
параллелен вектору
.
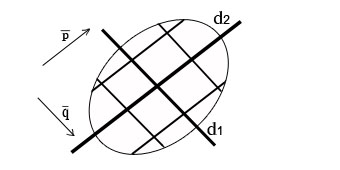
Рис.30. Диаметр сопряжен с вектором , а диаметр параллелен вектору .
Доказательство.
Пусть известны
координаты векторов
и
,
где вектор
параллелен
диаметру
(рис.30). Запишем уравнения диаметров
и
:
,
.
В этих уравнениях выделим коэффициенты при и . Получим уравнения диаметров в другом виде.
,
.
Пусть
и
направляющие векторы этих диаметров.
Тогда можно записать координаты векторов:
,
.
Так как диаметр
параллелен вектору
,
то и вектор
параллелен вектору
,
поэтому выполняется равенство
.
(2)
Раскрыв определитель в (2) и сгруппировав слагаемые с p1 и p2, получаем:
,
что равносильно определителю
.
(3)
Равенство (3)
является условием коллинеарности
векторов
и
,
значит, диаметр
параллелен вектору
.
Два диаметра центральной линии второго порядка называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру. На рисунках 31, 32, 33 изображены сопряженные диаметры d1 и d2 эллипса, окружности и пары пересекающихся прямых.
d1
d2
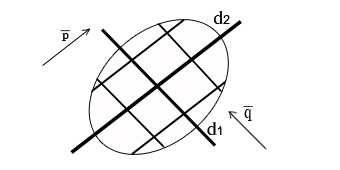
Рис.31. Сопряженные диаметры эллипса.
d1
d2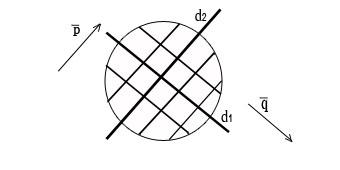
Рис.32. Сопряженные диаметры окружности.
d1
d2
Рис.33. Сопряженные
диаметры пары пересекающихся прямых.
