§15. Пересечение линии второго порядка с прямой

Пусть в аффинной системе координат линия второго порядка задана общим уравнением

, (1)

а прямая d параметрическими уравнениями

, , (2)

где p₁, p₂ - координаты направляющего вектора , , - координаты точки M₀ ,t - параметр. Найдем точки пересечения прямой d с линией .

Подставив x и y из (2) в уравнение (1) и выполнив алгебраические преобразования, получим уравнение вида:

, (3)

где

,

,

.

Решая уравнение (3), найдем значения параметров t, соответствующих точкам пересечения d с . Исследуем уравнение (3). Возможны два случая:

1) . Уравнение (3) будет квадратным и иметь два корня: или действительные различные, или действительные совпадающие, или мнимые различные. Поэтому точек пересечения прямой d с линией будет две (рис.25).

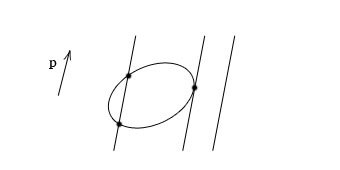
Рис.25. Прямые, параллельные вектору , имеют две точки пересечения с линией второго порядка.

2) . В этом случае уравнение (3) примет вид:

. (4)

Получили линейное уравнение относительно параметра t. В зависимости от значений коэффициентов этого уравнения получим три подслучая.

а) Если , то прямая d пересекает линию в одной точке с параметром (рис.26).

d

d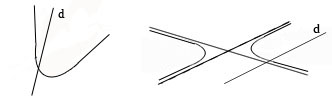

Рис.26. Прямые, пересекающие линию второго порядка в одной действительной точке.

б) Если , а , то получим уравнение 0∙t+R=0, которое не имеет корней. Значит, прямая d не имеет с линией ни одной общей точки (рис.27).

d

d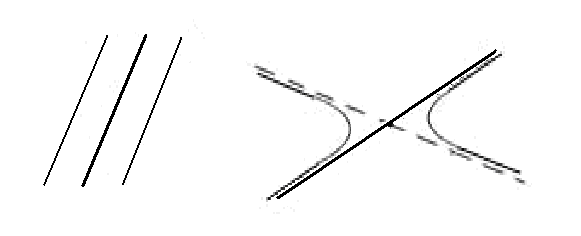

Рис.27. Прямые, не имеющие с линией второго порядка ни одной общей точки.

в) Если и , то уравнение (4) примет вид 0∙t+0=0, значит, прямая d имеет с линией бесконечное множество общих точек, т.е. или d совпадает с (рис.28).

d

d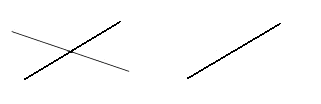

Рис.28. Прямые, имеющие с линией второго порядка бесконечное множество общих точек

Так как коэффициент P в уравнении (3) зависит только от координат p₁ и p₂ направляющего вектора и не зависит от координат точки M₀, то, следовательно, при все прямые, имеющие направление вектора , пересекают линию в двух точках (действительных различных, действительных совпадающих или мнимых комплексно-сопряженных).

Если , то либо прямая d содержится в , либо прямая d пересекает не более чем в одной точке.

§16. Асимптотические направления линии второго порядка. Асимптоты

Пусть линия задана общим уравнением

. (1)

Направление, определяемое ненулевым вектором , называется асимптотическим направлением относительно линии , если прямая, имеющая направление вектора , имеет с линией не более одной общей точки или содержится в линии .

Из §15 следует, что для того, чтобы направление, определяемое ненулевым вектором , было асимптотическим относительно линии второго порядка, заданной общим уравнением (1), необходимо и достаточно, чтобы выполнялось равенство: , т.е. чтобы

. (2)

Исследуем равенство (2). Возможно несколько случаев.

1. Пусть . Тогда из (2) следует, что , так как иначе и , что невозможно, так как . Разделим равенство (2) на и, использовав обозначение для углового коэффициента , получим уравнение для нахождения углового коэффициента:

.

Если - дискриминант этого уравнения, то

,

поэтому

.

Отсюда следует, что при количество асимптотических направлений линии зависит от значения инварианта I₂:

а) если , то линия не имеет асимптотических направлений;

б) если , то линия имеет два асимптотических направления;

в) если , то существует одно асимптотическое направление,

определяемое угловым коэффициентом , т.е. вектором .

2. Пусть . Тогда равенство (2) примет вид:

. (3)

В этом случае инвариант . Отсюда или .

а) Пусть , значит, . Равенство (3) примет вид: - любое действительное число. Следовательно, линия второго порядка будет иметь единственное асимптотическое направление, определяемое вектором .

б) Пусть , значит, . Равенство (3) преобразуем так:

(4)

З

любое действительное число.

десь во втором равенстве , так как иначе обратится в нуль и . Поэтому, разделив второе равенство в (4) на , получим:

Последним условиям удовлетворяют координаты двух векторов и , определяющих два асимптотических направления линии второго порядка, заданной уравнением (1).

Из определения асимптотического направления линии второго порядка следует, что оно не зависит от выбора системы координат. Поэтому количество асимптотических направлений можно исследовать по каноническим уравнениям линий.

1) Для эллипса инвариант , поэтому у эллипса нет асимптотических направлений. Условие выполняется также для мнимого и вырожденного эллипсов. Таким образом, линии эллиптического типа не имеют асимптотических направлений.

2) Для гипербол и пары пересекающихся прямых инвариант . Следовательно, линии гиперболического типа имеют два асимптотических направления. Найдем их, составив равенство вида (2): . Здесь , т.к. иначе и , поэтому, разделив последнее равенство на , получим: .

Значит, асимптотические направления линии гиперболического типа совпадают с направлениями асимптот гиперболы.

3) Для параболы инвариант . Значит, парабола имеет одно асимптотическое направление. Найдем его. Условие (2) для параболы примет вид:

Получаем, что , а - любое действительное число. Следовательно, вектор определяет асимптотическое направление данной параболы. Это направление совпадает с направлением оси симметрии параболы.

4) Для параллельных прямых инвариант , поэтому параллельные прямые имеют одно асимптотическое направление, совпадающее с направлением вектора , т.е. с направлением самих прямых. Итак, линии параболического типа имеют одно асимптотическое направление.

Лемма. Вектор имеет асимптотическое направление относительно линии параболического типа, заданной общим уравнением (1), тогда и только тогда, когда его координаты удовлетворяют условиям:

(5)

Доказательство. 1. Пусть вектор имеет асимптотическое направление. Покажем, что его координаты удовлетворяют системе (5). Для линии параболического типа инвариант , поэтому асимптотическое направление определит или вектор , если , или вектор , если . Подставим координаты вектора в систему (5):

Получили верные равенства. Подставим координаты вектора в cистему (5):

Так как в этом случае из равенств и следует, что , то получили верные равенства.

2. Обратно, пусть координаты ненулевого вектора удовлетворяют равенствам (5). Умножив первое равенство системы (5) на , второе - на и сложив, получим:

Получили условие, определяющее асимптотическое направление вектора .

Асимптотой линии второго порядка называется всякая прямая, которая либо всеми точками принадлежит этой линии, либо не имеет с ней ни одной общей точки (действительной или мнимой).

Из определения асимптоты следует, что для линии (1) прямая

(6)

будет асимптотой тогда и только тогда, когда в уравнении

(7)

коэффициенты и равны нулю одновременно, а - произвольное действительное число. Значит, всякая асимптота должна иметь асимптотическое направление, поэтому асимптоты могут существовать только для линий гиперболического и параболического типов.

Теорема 1. Если вектор имеет асимптотическое направление относительно линии, заданной уравнением (1), то для того, чтобы точка лежала на некоторой асимптоте, имеющей направление вектора , ее координаты должны удовлетворять уравнению

. (8)

Доказательство. 1.Пусть точка лежит на асимптоте, имеющей направление вектора . Примем эту точку за начальную, а переменную точку обозначим через . Параметрические уравнения асимптоты будут иметь вид:

(9)

Параметры точек пересечения с линией (1) определятся из условия (7). Так как для асимптоты , то условие будет иметь вид (8).

2.Обратно, пусть координаты точки удовлетворяют уравнению (8). Проведем через эту точку прямую d, параллельную вектору . Пусть уравнение этой прямой имеет вид (9), а параметры точек пересечения определяются уравнением (7). Так как вектор имеет асимптотическое направление, то в уравнении (7) коэффициент . И так как для точки выполняется условие (8), то и . Условия определяют асимптоту.

Теорема 2. Линии эллиптического типа и парабола не имеют асимптот; линии гиперболического типа имеют две асимптоты, соответствующие двум различным асимптотическим направлениям; линии параболического типа, отличные от параболы и являющиеся парой параллельных прямых (действительных или мнимых), имеют множество параллельных асимптот, включая данные прямые.

Доказательство. Уравнение асимптоты, имеющей направление вектора , имеет вид (8).

Запишем это уравнение иначе:

. (10)

1) Так как линии эллиптического типа не имеют асимптотических направлений, то, следовательно, не имеют и асимптот.

2) Линии гиперболического типа имеют два асимптотических направления, например, и . Исследуем одно из них: . В уравнении (10) выражения и не равны нулю одновременно, так как иначе, согласно лемме, линия будет параболического типа. Таким образом, уравнение (10) задаёт одну и только одну асимптоту направления . Аналогичные рассуждения для другого асимптотического направления . Итак, линия гиперболического типа имеет две асимптоты.

3) Линии параболического типа имеют одно асимптотическое направление. Пусть оно задано вектором . Это может быть вектор при или вектор при .

Для линии параболического типа, согласно лемме, выражения и равны нулю одновременно. Поэтому уравнение (10) примет вид:

, (11)

где

. (12)

Отсюда следует, что, если , то уравнение (11) не имеет корней, значит, линия (1) не имеет асимптот, параллельных вектору ; если , то уравнение (11) имеет множество корней, то есть все прямые, параллельные вектору , являются асимптотами линии второго порядка. Так как понятие асимптот не зависит от выбора системы координат, а имеет геометрический смысл, то найдем число по каноническим уравнениям линий.

а) Возьмем параболу . Так как в этом уравнении , то асимптотическое направление задает вектор . Из выражения (12) найдем : . Итак, асимптот парабола не имеет.

б) Возьмем параллельные прямые, заданные уравнениями . Здесь , значит, асимптотическое направление определяется вектором кроме того a₁₀=a₂₀=0. Вычислим значение по формуле (12) и получим: . Поэтому для пары параллельных прямых (действительных различных, действительных совпадающих или мнимых) любая прямая, параллельная вектору асимптотического направления, а, значит, и самим прямым, является асимптотой, в том числе и сами параллельные прямые.