§13. Приведение уравнения линии второго порядка к простейшему виду при помощи параллельного переноса системы координат

Теорема. Если в общем уравнении линии второго порядка коэффициент а₁₂=0, то с помощью параллельного переноса осей координат уравнение линии можно привести к одному из следующих видов:

А +В +С=0, А 0, B 0, (I)

А , А , (II)

А + С=0, А . (III)

где , - координаты произвольной точки линии относительно новой системы координат.

Доказательство. По условию теоремы уравнение линии имеет вид:

а₁₁х²+а₂₂у²+2а₁₀х+2а₂₀у+а₀₀=0. (1)

Применим преобразование параллельного переноса осей координат по формулам:

х = ,

у= ,

где x₀, y₀ - координаты начала новой системы координат .

Возможно 3 случая:

1. а₁₁ а₂₂ .

В уравнении (1) сгруппируем слагаемые с х и дополним их до полного квадрата, затем сгруппируем слагаемые с у и также дополним до полного квадрата. Получим:

а₁₁(х² + 2 х +( )² - ( )²) + а₂₂(у² + 2 у + ( )² - ( )²)+а₀₀=0.

Отсюда получаем:

а₁₁(х+ )² + а₂₂(у+ )² - - + а₀₀ = 0. (2)

Введём новые переменные:

=х+ , х = - ,

(3)

=у+ . у = - .

Введение новых переменных по формулам (3) равносильно переходу к новой системе координат, полученной из старой параллельным переносом в новое начало (- ,- ).

Обозначив свободный член уравнения (2) через С, а₁₁ - через А, а₂₂ - через В, из (2) получим уравнение:

А =0. (I)

2. а₂₂=0, а₂₀ 0 (или а₁₁=0, а₁₀ 0). Уравнение (1) примет вид:

а₁₁х²+2а₁₀х+2а₂₀у+а₀₀=0.

Выполним следующие алгебраические преобразования:

а₁₁(х² + 2 ) - + 2а₂₀у +а₀₀ = 0;

а₁₁(х + )² +2а₂₀(у + ) = 0. (4)

Произведя перенос осей координат по формулам

х = - ,

у

(- ).

= - , найдем начало новой системы координат

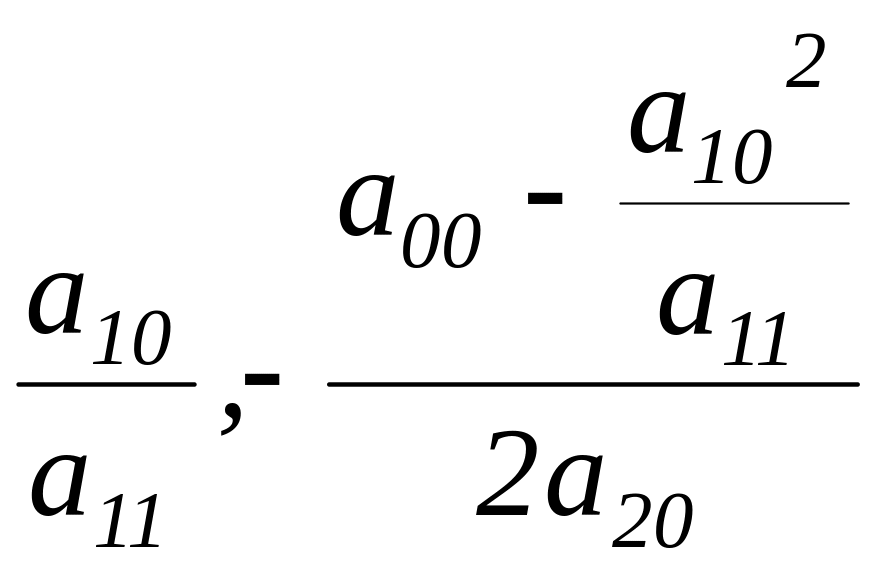Введя обозначения а₁₁=А, 2а₂₀=D, из уравнения (4) получим уравнение:

А +D = 0. (II) 3. а₂₂=0, а₂₀=0 (или а₁₁=0, а₁₀=0).

Уравнение (1) примет вид:

а₁₁х² +2а₁₀х + а₀₀ =0 а₁₁(х+ )² + а₀₀ - =0.

Перенося оси координат по формулам

х= - , найдем (- )

у= ,

и, вводя обозначения а₁₁=А, а₀₀ - =С, получим уравнение:

А + С=0. (Ш)

Пример. Привести к простейшему виду, записать формулы преобразования координат точек и построить линию, заданную уравнением

2х² - 8х + 4у +12 = 0. (5)

Решение. Так как а₁₂=0, то применим преобразование параллельного переноса осей координат. Дополним до полного квадрата слагаемые с переменной x:

2(х² - 4х + 4-4) +4у+12 = 0,

2(х-2)² -8 +4у+12 = 0,

2(х-2)² +4(у+1) = 0,

введем новые переменные:

=х-2, =у+1. х= +2, у= -1 =(2,-1).

Уравнение линии примет вид:

.

Получили уравнение параболы, параметр которой р=1, 0,

F(0,- ), D(0, ).

Точки F и D заданы относительно новой системы координат .

П

остроим линию.

y

x

1

2

O

D

-1

F

Рис.17.Парабола, заданная уравнением (5).