§12. Общее уравнение линии второго порядка и приведение его к простейшему виду при помощи поворота системы координат

Ясно, что одна и та же линия в разных системах координат определяется разными уравнениями, но остаётся неизменным (инвариантным) порядок линии. Во введении дано определение и общее уравнение линии второго порядка вида:

а₁₁х²+2а₁₂ху+а₂₂у²+2а₁₀х+2а₂₀у+а₀₀=0. (1)

Коэффициенты а_ij этого уравнения - любые действительные числа, но а₁₁, а₁₂, а₂₂ не равны нулю одновременно. Будем также считать, что а_ij=a_ji.

При решении многих задач бывает необходимым по уравнению (1) определить вид линии. Наиболее общий способ решения этой задачи состоит в переходе от одной системы координат к другой.

Будем считать, что линия (1) задана в прямоугольной системе координат на евклидовой плоскости.

Теорема. Пусть линия второго порядка задана в прямоугольной системе координат уравнением (1), в котором коэффициент а₁₂ 0. Тогда существует такая прямоугольная система координат, полученная из данной с помощью поворота вокруг начала координат на некоторый угол α, в которой уравнение (1) приводится к виду, не содержащему произведения переменных.

Доказательство. Повернём оси системы координат O , вокруг точки О на угол α . Получим новую систему координат О ' ' (рис.15). Формулы поворота прямоугольной системы координат вокруг начала координат имеют вид:

х =х'cosα–y'sinα,

(2)

y=x'sinα+y'cosα.

y

x^

y

0

α

x

Рис.15. Поворот системы координат Oij, вокруг точки О на угол α.

Чтобы получить уравнение линии (1) относительно новой системы координат, подставим х и у из формул (2) в уравнение (1). После раскрытия скобок и приведения подобных членов с переменными получим уравнение линии в новой системе координат О ' ' в виде:

а₁₁' (х')²+2а₁₂'х'у'+а₂₂' (у')²+2а₁₀'х'+2а₂₀'у'+а₀₀'=0, (3)

где

а₁₁'=а₁₁cos²α+2a₁₂cosαsinα+a₂₂sin²α,

a₁₂'=-a₁₁sinαcosα+a₁₂cos²α–a₁₂sin²α+a₂₂sinαcosα,

a₂₂'=a₁₁sin²α-2a₁₂sinαcosα+a₂₂cos²α, (4)

a₁₀'=a₁₀cosα+a₂₀sinα,

a₂₀'=-a₁₀sinα+a₂₀cosα,

a₀₀'=a₀₀.

Свободный член а₀₀ при повороте системы координат не изменяется, он является инвариантом поворота. Так как поворот является ортогональным преобразованием, то инвариантными являются выражения

I₁=а₁₁+а₂₂ и I₂ = а₁₁ а₁₂ = а₁₁а₂₂ – а₁₂².

а₂₁ а₂₂

Потребуем, чтобы выполнялось условие: а₁₂'=0, т.е.

-а₁₁sinαcosα + a₁₂cos²α – a₁₂sin²α + a₂₂sinαcosα = 0.

Отсюда

-sinα (a₁₁cosα + a₁₂sinα) + cosα (a₁₂cosα + a₂₂sinα) = 0.

Выражение, стоящее в левой части последнего равенства, запишем в виде определителя и получим:

a₁₁cosα + a₁₂sinα a₁₂cosα + a₂₂sinα = 0.

cosα sinα

Т ак как определитель равен нулю, то его строки пропорциональны. Поэтому существует такое число λ, что

a₁₁cosα + a₁₂sinα = λcosα,

(5)

a₁₂cosα + a₂₂sinα = λsinα,

(a₁₁ – λ)cosα + a₁₂sinα = 0,

(6)

a₁₂cosα + (a₂₂ – λ)sinα = 0.

Система (6) однородных уравнений имеет ненулевое решение при условии:

а₁₁ – λ а₁₂

= 0,

а₁₂ а₂₂ – λ

что равносильно уравнению

λ² – (а₁₁ + а₂₂)λ + а₁₁а₂₂ – а₁₂² = 0 , (7)

т.е. уравнению

λ² - I₁λ + I₂ = 0. (8)

Так как I₁ и I₂ в уравнении (8) являются ортогональными инвариантами, т.е. не зависят от выбора прямоугольной системы координат, то и корни уравнения (8) также не зависят от выбора прямоугольной системы координат. Поэтому уравнение (8), азывается характеристическим уравнением линии второго порядка.

Найдём дискриминант уравнения (7),а значит и уравнения (8)

D = ( a_{11 +} a₂₂)² - 4( a₁₁a₂₂ - a₁₂²) = ( a₁₁ - a₂₂)² + 4a₁₂².

Так как а₁₂ 0, то D>0, поэтому корни λ₁ и λ₂ уравнения (7)- действительные и различные.

Из первого уравнения системы (6) при λ=λ₁ находим

tgα₁ = , (9)

а при λ = λ₂ находим

tgα₂ = . (10)

По теореме Виета для уравнений (7) и (8)λ₁+λ₂=I₁=а₁₁+а₂₂, λ₁λ₂=I₂=а₁₁а₂₂-а₁₂² поэтому

tgα₁tgα₂ = = =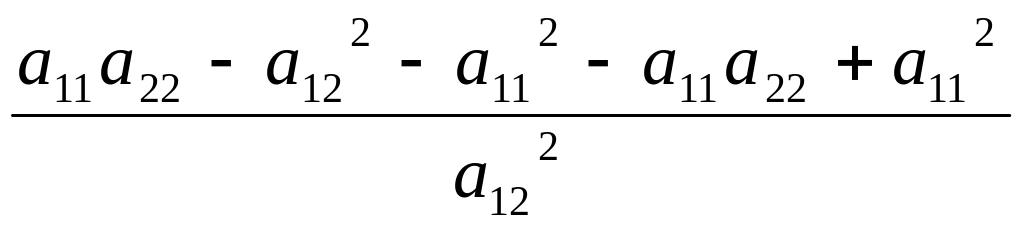 -1.

Отсюда следует, что прямые с угловыми коэффициентами k₁=tgα₁ и k₂=tgα₂ взаимно перпендикулярны. Примем направления этих прямых за направления новых осей прямоугольной системы координат О. . Пусть tgα=tgα₁ определяет направление оси Ох^', запишем координаты векторов

и :

(cosα,sinα), '(cos(90º+α),sin(90º+α)),т.е. '(-sinα,cosα). Тригонометрические функции cosα и sinα можно найти по известным формулам через tgα:

cosα= , sinα= .

Знак перед радикалом выбирается произвольно, но одинаково в обеих формулах.

Итак, при повороте системы координат Оij на угол α, определяемый условием (9) при α₁=α, коэффициент а₁₂^' в уравнении линии относительно новой системы координат О обратится в нуль.

Найдём коэффициенты а₁₁' и а₂₂^'.

Используем выражения для а₁₁' из формул (4). Преобразовав его и применив формулы (5) при λ= λ₁, получим:

а₁₁^'=cosα(a₁₁cosα+ a₁₂sinα)+sinα(a₂₁cosα+ a₂₂sinα)=λ₁cos²α+λ₁sin²α=λ₁. Так как а₁₁'+а₂₂^'=а₁₁+а₂₂ и а₁₁+а₂₂=λ₁+λ₂, то а₂₂'=а₁₁+а₂₂-а₁₁^'=λ₁+λ₂-λ₁=λ_.2. Таким образом, уравнение (3) линии второго порядка относительно новой системы координат О примет вид:

λ₁(х')²+λ₂(у')²+2а₁₀'х'+2а₂₀'у^'+а₀₀=0. (11)

Получили уравнение, в котором отсутствует член с произведением переменных.

Пример. Привести к каноническому виду уравнение

5х²+8ху+5у²-9=0. (12)

Построить линию и записать формулы преобразования координат точек.

Решение. Так как в заданном уравнении коэффициент а₁₂=4, т.е. не равен 0, то применяем преобразование поворота системы координат.

1. Выпишем коэффициенты уравнения и найдем инварианты I₁ и I₂:

а₁₁=5, а₁₂=4, а₂₂=5, а₁₀=0, а₂₀=0, а₀₀=9, I₁=а₁₁+а₂₂=10, I₂=9.

2. Составим характеристическое уравнение и найдём его корни:

λ² -I₁λ +I₂=0, λ² -10λ +9 = 0. Отсюда λ₁=1, λ₂=9.

3. Найдём направление новых осей координат:

tgα= = =-1 α=-45º, sinα= , cosα= .

(cosα,sinα)=( , ) (1,-1) определяет направление оси Ох^'.

'(sinα,cosα)=( , ) (1,1) определяет направление оси Оу'.

4. Найдём новые коэффициенты а₁₀' и а₂₀^' по формулам из (4):

а₁₀^'=0, а₂₀^'=0. 5. Запишем уравнение линии в новой системе координат:

. Получили уравнение эллипса, полуоси которого а=3, b=1.

6. Построим линию.

y

y^

A₂

B₁

x



B₂

0

A₁

Рис.16. Эллипс, заданный уравнением (12).

7. Запишем формулы преобразования координат точек в виде (2):

х= ,

у= .