39) Среднегодовой темп роста и прироста.Средний уровень динамического ряда,абсолютное значение 1% прироста.
Среднегодовой темп роста показывает во сколько раз в среднем за год изменился данный показатель.
Среднегодовой темп роста исчисляется в след последовательности
сначала по формуле средней геометрической исчисляют среднегодовой коэффициент роста (снижения) — Kp=
на базе среднегодового коэффициента определяют среднегодовой темп роста путем умножения коэффиицента на 100%
Среднегодовой темп прироста определяется путем вычитания из темпа роста 100%.Тпр=Тр-100
Средний уровень ряда определяется по средней арифметической или средней хронологической
Абсолютное
содержание одного процента прироста
1%=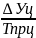
1%=0,01уi-1
40)Приведение динамических рядов к одному основанию. Метод скользящей средней
В экономической практике часто возникает необходимость сравнения между собой нескольких рядов динамики (например, показатели динамики производства электроэнергии, производства зерна, продажи легковых автомобилей и др.). Для этого нужно преобразовать абсолютные показатели сравниваемых рядов динамики в производные ряды относительных базисных величин, приняв показатели какого-либо одного года за единицу или за 100%.Такое преобразование нескольких рядов динамики называется приведением их к одинаковому основанию. Теоретически за базу сравнения может быть принят абсолютный уровень любого года, но в экономических исследованиях для базы сравнения надо выбирать период, имеющий определенное экономическое или историческое значение в развитии явлений.
Из группы методов скользящего среднего самым простым является метод простого скользящего среднего по n-узлам. В этом методе среднее фиксированного числа n-последних наблюдений используется для оценки следующего значения уровня ряда.
Значение прогноза, полученного методом простого скользящего среднего, всегда меньше фактического значения — если исходные данные монотонно возрастают, и наоборот больше фактического значения — если исходные данные монотонно убывают. Поэтому с помощью простого скользящего среднего нельзя получить точных прогнозов. Этот метод лучше всего подходит для данных с небольшими случайными отклонениями от некоторого постоянного или медленно меняющегося значения.
Ỹt= α0Υt+ α1Υt+1 +α2Υt+2
Метод скользящей средней основан на свойстве средней погашать случайные отклонения от общей закономерности. Расчет скользящей средней осуществляется по средней арифметической простой из заданного числа уровней ряда, с отбрасыванием, при вычислении каждой новой средней, предыдущего уровня и присоединением следующего. Сглаживание методом простой скользящей средней заключается в том, что вычисляется средний уровень из 3, 5, 7 и т.д. уровней. В результате, расчет средней, как бы, скользит от начала ряда динамики к его концу. При нечетном шаге каждая вычисленная скользящая средняя соответствует реальному интервалу (моменту) времени, находящемуся в середине шага (интервала), а число сглаженных уровней, меньше первоначального числа уровней на величину шага скользящей средней, уменьшенного на единицу. Например, формула для расчета 5-месячной скользящей средней будет выглядеть следующим образом:
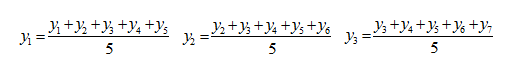
Если шаг скользящей средней выражен четным числом, то полученные скользящие средние центрируют. Операция центрирования заключается в повторном скольжении с шагом, равным двум. Число уровней сглаженного ряда будет меньше на величину шага скользящей средней.
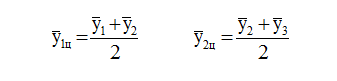
Определение интервала сглаживания (числа входящих в него уровней) зависит:
если необходимо сгладить беспорядочные колебания, то интервал сглаживания берут большим (до 5-7 уровней);
если же есть необходимость сохранить периодически повторяющиеся колебания, то интервал сглаживания уменьшают до 3 уровней.