23)Понятие моды.Расчет моды для дискретного и интервального ряда распределения.

Мода это наиболее часто встречающаяся варианта ряда распределения. Мода дискретного ряда определяется визуально.

Разряд	Число рабочих	Накопленные частоты
1	2	2
2	4	6
3	6	12
4 Мода и медиана	18	30
5	10	40
6	6	46

Мода интервального ряда определяется по формуле:

М₀=Х₀+i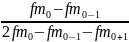

Где Х₀ нижняя граница модального интервала.

fm₀ – частота модального интервала

fm_0-1 – частота интервала предшествующего модальному

fm₀₊₁ – частота интервала следующего за модальным

Модальным называется интервал имеющий наибольшую частоту.

Стаж работы	Количество работников	Накопленные частоты
Менее 1	5	5
1-3	15	20
3-5	20	40
5-10 мод интервал	25	65
10 и выше	5	70
Всего	70

М₀=5+5*25-20/2*25-20-25=6

24) Понятие медианы. Расчет медианы для дискретного и интервального ряда.

Медиана – это варианта которая приходится на середину ряда распределения.

Медианным называется интервал на который приходится полусумма накопленных частот

М_е=X₀+i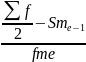

Где Х₀ – нижняя граница медианного интервала

i – величина медианного интервала

Σf/2 – полусумма накопленных частот

Sm_e-1 – сумма накопленных частот интервала предшествующего медианному

Fme – частота медианного интервала

Стаж работы	Количество работников	Накопленные частоты
Менее 1	5	5
1-3	15	20
3-5 мед интервал	20	40
5-10	25	65
10 и выше	5	70
Всего	70

Ме=3+2*(70/2-20)/20=4,5

25) Понятие вариации. Среднее линейное отклонение и размах вариации.

Вариация – это колебание признаков под воздействием факторов.

R=X_max – X_min

Среднее линейное отклонение.

Средняя арифметическая абсолютных величин отклонений варианты от средней

D=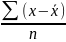 простая

D=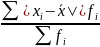 взвешенная

Вид продукции	Себестоимость	Объем
А	80	200
Б	90	300
С	110	500
Д	120	150
Итого		1150

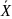=(80*200+90*30+40*500+120*150)/1150=102,4

D=|80-102.4|*200+|90-102.4|*300+|110-102.4|*500+|120-102.4|*150/1150=13.12

26) Понятие дисперсии.Способы определения дисперсии и ее свойства.

Дисперсия – средний квадрат отклонений варианты от средней.

ʓ²=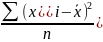 простая

ʓ²=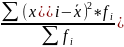 взвешенная

Свойства дисперсии

1. Если все варианты увеличить в К раз, то дисперсия увеличится в К² раз

2. Увеличение или уменьшение варианты на одно и то же число не изменяет дисперсию.

3. Дисперсия относительно средней арифметической равна дисперсии относительно произвольно постоянной без квадрата разности между средней арифметической и вариантой

4. Дисперсия равна средней арифметической квадратов варианты без квадратов средней арифметической.

ʓ²=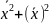

ʓ²=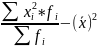

5. Если все частоты увеличить или уменьшить в несколько раз то дисперсия не изменится.