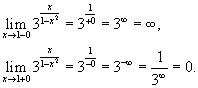- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
17. Точки разрыва функции и их классификация.
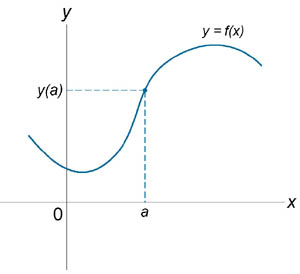
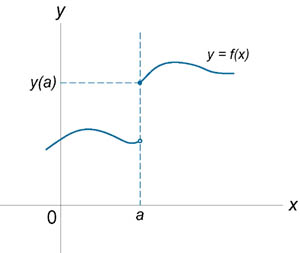
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая точка
называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. |
|||||||||||||||
Пример 1 |
|||||||||||||||
|
|||||||||||||||
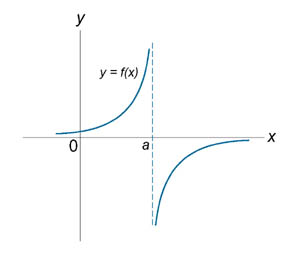
Исследовать
функцию Решение. Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода. Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода. |
|||||||||||||||
18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
Теорема 4.1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная.
Теорема 4.2. Произведение конечного числа непрерывных функций есть функция непрерывная.
С л е д с т в и е. Целый полином Р(х)=а0+а1х+... +аnхn есть функция непрерывная.
Теорема 4.3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля.
Теорема 4.4. Непрерывная функция от непрерывной функции есть функция непрерывная.
Теорема 4.5. Если y = f(x) непрерывна и строго монотонна на промежутке <а,b> , то существует обратная функция х = j(y), определенная на промежутке < f(a), f(b) >, причем последняя также монотонна и непрерывна в том же смысле.