13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.

Не всякая функция имеет предел, даже будучи ограниченной. Например, sin x при x   предела не имеет, хотя   1.  Укажем два признака существования предела функции.  Теорема (о промежуточной функции).  Пусть в некоторой окрестности О (а) точки а функция f(x) заключена между двумя функциями  (x) и  (x), имеющими одинаковый предел А при x  a, то есть  (x)  f(x)   (x) и   Тогда функция f(x) имеет тот же предел:   Функция f (x) называется возрастающей на данном множестве X, если f(x1)<f(x2) для x1< x2 (x1, x2  X).  Функция f(x) называется убывающей на множестве X, если f( ) > f(x2) для x1< x2 (x1, x2  X).  Возрастающая или убывающая функция называется монотонной на данном множестве X.  Если f( )  f( ) для x1< x2, то f(x) называют неубывающей, а если f(x1)  f(x2) для x1< x2 – не возрастающей. И в этом случае функцию называют монотонной.  Теорема. Пусть функция f(x) монотонна и ограничена при x a (или при x  a). Тогда существует соответственно   (или  ).

14. Первый замечательный предел

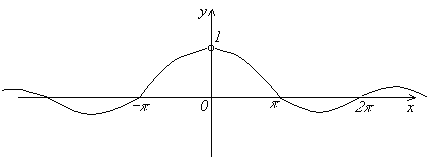
Функция   не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.

О днако, можно найти предел этой функции при х→0.

Приведем доказательство записанной формулы. Рассмотрим окружность радиуса 1 и предположим, что угол α, выраженный в радианах, заключен в пределах 0 < α < π/2. (Так как   четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α > 0.) Из рисунка видно, что

S_ΔOAC <S_сект.OAC <S_ΔOBC.

Так как указанные площади соответственно равны

S_ΔOAC=0,5∙OC∙OA∙sinα=0,5sinα,S_сект.OAC=0,5∙OC²∙α=0,5α,S_ΔOBC=0,5∙OC∙BC=0,5tgα.

Следовательно,

sin α < α < tg α.

Разделим все члены неравенства на sin α > 0:

.

Но  . Поэтому на основании теоремы 4 о пределах заключаем, что  .

Выведенная формула и называется первым замечательным пределом.

Таким образом, первый замечательный предел служит для раскрытия неопределенности  . Заметим, что полученную формулу не следует путать с пределами  .

Примеры.

1. .

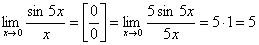15. Второй замечательный предел

Второй замечательный предел служит для раскрытия неопределенности 1^∞ и выглядит следующим образом

Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

Примеры.

1. .

2. .

3. .

4. 

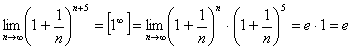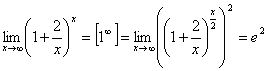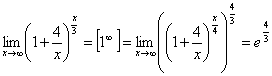
16. Непрерывность функции в точке, в интервале, на отрезке.