17.2. Связь между функцией, ее пределом и бесконечно малой функцией

Теорема 17.5. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).

▼ Пусть     

Следовательно, т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲  

Теорема 17.6 (обратная). Если функцию ƒ(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции ƒ(х), т. е. если ƒ(х)=А+α(х), то lim ƒ(х)=А при Х→Хо

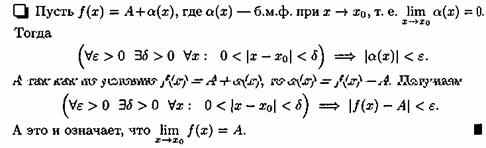
11.Связь между функцией, ее пределом и бесконечно малой функцией.

Теорема 17.5. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).

▼ Пусть     

Следовательно, т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲  

Теорема 17.6 (обратная). Если функцию ƒ(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции ƒ(х), т. е. если ƒ(х)=А+α(х), то lim ƒ(х)=А при Х→Хо

<< Пример 17.2

Доказать, что

Решение: Функцию 5+х можно представить в виде суммы числа 7 и б.м.ф. х-2 (при х→2), т. е. выполнено равенство 5+х=7+(х-2). Следовательно, по теореме 17.6 получаем

12.Основные теоремы о пределах

Рассмотрим теоремы, которые облегчают нахождение пределов функции. Формулировка и доказательство теорем для случаев, когда х→x₀ и х→∞, аналогичны. В приводимых теоремах будем считать, что пределы limƒ(х), limφ(х) существуют при Х→Хо

Теорема 17.7. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

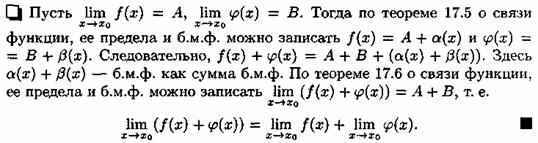
В случае разности функций доказательство аналогично. Теорема справедлива для алгебраической суммы любого конечного числа функций.

Следствие 17.3. Функция может иметь только один предел при х→х_о.

Пусть По теореме 17.7 имеем:

Отсюда А-В=0, т. е. А=В.

Теорема 17.8. Предел произведения двух функций равен произведению их пределов:

Доказательство аналогично предыдущему, проведем его без особых пояснений. Так как

где α(х) и ß(х) — б.м.ф. Следовательно,

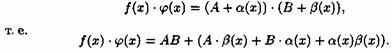
Выражение в скобках есть б.м.ф. Поэтому

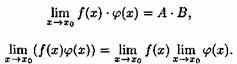
Отметим, что теорема справедлива для произведения любого конечного числа функций.  

Следствие 17.4 . Постоянный множитель можно выносить за знак предела: ▼ ▲

Следствие 17.5 . Предел степени с натуральным показателем равен той же степени предела:

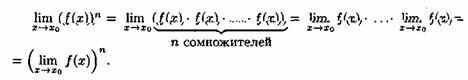
Теорема 17.9. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:

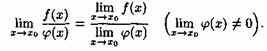
Доказательство аналогично предыдущему. Из равенств

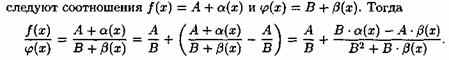
Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел.

 Пример 17.3

Вычислить 

Решение: