
- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
7.Теоремы о предельных переходах в неравенствах.
Теорема
1. Пусть ![]() -
сходящаяся последовательность и
-
сходящаяся последовательность и ![]() .
Тогда
.
Тогда ![]() .
.
Доказательство этой теоремы проведем методом от противного.
Обозначим ![]() .
Тогда утверждение, противоположное
доказываемому, имеет вид:
.
Тогда утверждение, противоположное
доказываемому, имеет вид:
![]() .
.
Возьмем![]() .
Тогда, по определению, предела
последовательности, можно написать
.
Тогда, по определению, предела
последовательности, можно написать
![]() .
.
Последнее неравенство распишем в виде двойного
![]()
Но
так как
,
то ![]() и
получается что
и
получается что ![]() ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
Следствие.
Если
и ![]() сходящиеся
последовательности и
сходящиеся
последовательности и ![]() ,
то
,
то
![]() .
.
Доказательство дается следующей цепочкой следствий
![]() =>
=> ![]() =>
=> ![]() =>
=> ![]()
=>
Важное
замечание. Допустим, что в условии
теоремы вместо
мы
написали![]() .
Можно ли утверждать, что
.
Можно ли утверждать, что ![]() ?
?
Ответ
отрицательный. Действительно, пусть,
например, ![]() .
Тогда
.
Тогда ![]() ,
но
,
но ![]() .
.
Таким образом, итог этой теоремы и замечание выглядит так: в неравенствах допустим предельный переход, надо только иметь ввиду, что после предельного перехода строгое неравенство (типа > или <) может замениться на нестрогое
(>
перейдет в ![]() ,
< перейдет в
,
< перейдет в ![]() ).
).
Теорема 2. Пусть
и
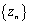 сходящиеся
последовательности;
сходящиеся
последовательности;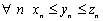 ;
;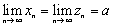
Тогда
также
сходящаяся последовательность и ![]() .
.
Доказательство:
=> ![]()
или ![]()
![]() =>
=> ![]()
или![]() .
.
Беря ![]() и
учитывая, что
и
учитывая, что ![]()
![]() можно
записать
можно
записать ![]()
![]() .
.
Выбрасывая лишнее, получим что
![]() или
или ![]() ,
,
что
и говорит о том, что ![]() .
.
8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятиеимеет более строгое определение.
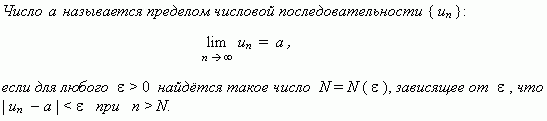
Это
определение означает, что a
есть предел числовой
последовательности, если её общий член
неограниченно приближается к a
при возрастании n.
Геометрически это значит, что для
любого ![]() >
0 можно
найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a
a
).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
>
0 можно
найти такое число N,
что начиная с n > N
все члены
последовательности расположены внутри
интервала ( a
a
).
Последовательность, имеющая предел,
называется сходящейся;
в противном случае – расходящейся.
Последовательность
называется ограниченной,
если существует такое число M,
что | un
| ![]() Mдля
всех n . Возрастающая
или убывающая последовательность
называется монотонной.
Mдля
всех n . Возрастающая
или убывающая последовательность
называется монотонной.
Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства).
Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если { un } и { vn } две сходящиеся последовательности, то:
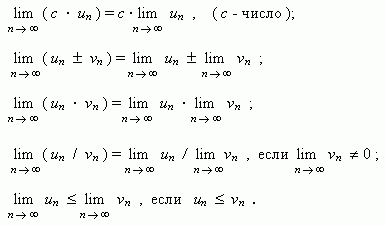
Если члены последовательностей { un }, { vn }, { wn } удовлетворяют неравенствам
![]()
9. Предел функции в точке. Односторонние пределы.
Пусть функция у=ƒ (х) определена в некоторой окрестности точки хо, кроме, быть может, самой точки хо.
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне).
Число А называется пределом функции у=ƒ(х) в топке x0 (или при х® хо), если для любой последовательности допустимых значений аргумента xn, n є N (xn¹x0), сходящейся к хопоследовательность соответствующих значений функции ƒ(хn), n є N, сходится к числу А
![]()
В этом
случае пишут ![]() или
ƒ(х)—>А при х→хо.
Геометрический смысл предела
функции:
или
ƒ(х)—>А при х→хо.
Геометрический смысл предела
функции: ![]() означает,
что для всех точек х, достаточно близких
к точке хо,
соответствующие значения функции как
угодно мало отличаются от числа А.
означает,
что для всех точек х, достаточно близких
к точке хо,
соответствующие значения функции как
угодно мало отличаются от числа А.
Определение 2 (на «языке ε», или по Коши).
Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все х¹хо, удовлетворяющих неравенству |х-хо|<δ, выполняется неравенство |ƒ(х)-А|<ε.
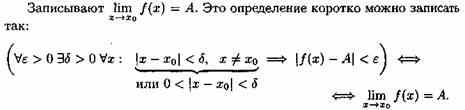
Геометрический смысл предела функции:
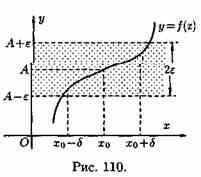
если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех х¹хо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
<< Пример 16.1
Доказать, что
![]()

Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3| < δ, выполняется неравенство |(2х-1)-5|<ε, т. е. |х-3|<ε.
Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|< δ, выполняется неравенство |(2х-1)-5|<ε. Следовательно, lim(2x-1)=5 при х –>3.
<< Пример 16.2
![]()
![]()
