
- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
5.Обратная функция. Сложная функция
1. Понятие о сложной функции Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у). |
Пример. Функцию |
Для
записи композиции функций употребляется
значок |
Пример.
Вычисляя
значения функции
,
необходимо брать только те числа х,
для которых |
2. Взаимно обратные функции Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями. |
3. График обратной функции Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат –их значения, то эти графики будут симметричны друг другу относительно прямой у = х. |
4. Свойства взаимно обратных функций Отметим некоторые свойства взаимно обратных функций. 1) Тождества. Пусть f и g – взаимно обратные функции. Тогда : f(g(y)) = у и g(f(x)) = х. 2) Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g. 3) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций. 4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой у = х. |
6. Числовая последовательность. Предел числовой последовательности
Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае
![]()
Числовой последовательностью называется бесконечное множество чисел
![]() (1)
(1)
следующих одно
за другим в определенном порядке и
построенных по определенному закону,
с помощью которого ![]() задается
как функция целочисленного
аргумента,
задается
как функция целочисленного
аргумента, ![]() т.е.
т.е. ![]() .
.
Число А называется
пределом последовательности (1), если
для любого ![]() существует
число
существует
число ![]() ,
такое, что при
,
такое, что при ![]() выполняется
неравенство
выполняется
неравенство ![]() . Если
число А есть предел последовательности
(1), то пишут
. Если
число А есть предел последовательности
(1), то пишут
![]()
Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.
Для сходящихся последовательностей имеют место теоремы:
![]()
![]()
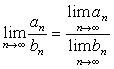
если ![]() .
.
