45. Производные и дифференциалы функций нескольких переменных.

Частной производной от функции   по независимой переменной   называется производная

, вычисленная при постоянном  .

Частной производной по y называется производная  , вычисленная при постоянном  . Для частных производных справедливы обычные правила и формулы дифференцирования.

Пример 1.  .

Рассматривая   как постоянную величину  , получим  .

Рассматривая   как постоянную величину  , получим  .

Пример 2. 

;  ;

;  .

Полным приращением функции   в точке   называется разность  , где   и   произвольные приращения аргументов. Функция   называется дифференцируемой в точке  , если в этой точке полное приращение можно представить в виде  , где  .

Полным дифференциалом функции   называется главная часть полного приращения  , линейная относительно приращений аргументов   и  , то есть  .

Полный дифференциал функции   вычисляется по формуле  .

Для функции трех переменных  .

При достаточно малом   для дифференцируемой функции   справедливы приближенные равенства  ;  , которые применяются для приближенного вычисления значения функции

. ()

Пример 3. Вычислить приближенное значение:  .

Решение. Полагая, что   есть частное значение функции   в точке   и что вспомогательная точка будет  , получим 

;  ;  ;  .

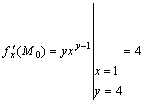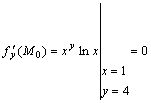Подставляя в формулу (), найдем:

.

Частными производными второго порядка от функции   называются частные производные от ее частных производных первого порядка.

Обозначения частных производных второго порядка:

;  ;

;  .

Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны:  .

Дифференциалом второго порядка от функции   называется дифференциал от ее полного дифференциала, то есть  . Если   и   – независимые переменные и функция   имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле  .

Пример 4.  . Найти  ,  ,  .

Решение. Найдем частные производные:  ;  . Дифференцируя повторно, получим  ;

;  .

46. Экстремум функций многих переменных.

Определение.  Пусть  функция  f (х, у)  определена в точке  M₀ (x₀, y₀)  и  в некоторой её окрестности. Функция  f (х, у)   имеет максимум в точке(x₀, y₀), если f  (x₀, y₀) >   f (х, у) для всех точек(х, у). из некоторой окрестности точки(x₀, y₀).    Если же f  (x₀, y₀) <  f (х, у)., то функция f (х, у) имеет минимум в точке M₀ (x₀, y₀). Точки, в которых функция принимает максимальное и минимальное значения, называются экстремальными.

        Аналогично вводятся понятия максимума и минимума для функций трёх и более аргументов. Мы ограничимся рассмотрением функций двух переменных. В случае необходимости весь изложенный ниже материал легко обобщается на случаи функций любого  числа переменных.

Теорема 1 (необходимые условия экстремума).                   Если  функция  f (х, у) имеет в точке M₀ (x₀, y₀) экстремум, то все частные производные первого порядка от f (х, у)  или  равны нулю, или не существуют в этой точке.

Доказательство.  Зафиксируем один аргумент функции f (х, у). Например, положим переменную у равной постоянной  y₀. Функция  f   (x, y₀)  будет в   этом случае функцией одной переменнойх. По условию теоремы при x = x₀ она имеет экстремум (максимум или  минимум) и, следовательно, её первая производная в этой точке равна 0 (см. тему №5), то есть  (или не существует). Рассуждая аналогично, убеждаемся, что производная функции f (x₀, y) по переменной у должна обращаться в нуль или не существовать при y = y₀. Теорема доказана.

        Данная теорема даёт необходимые условия существования экстремума: функция f (х, у) имеет экстремум в тех точках, где частные   производные первого порядка   и  обращаются в нуль (или не существуют).

        Сформулируем правило нахождения точек, в которых функция может иметь экстремум: приравнивая частные производные первого порядка к нулю, получаем систему уравнений:

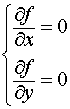
        Решения этой системы, а также точки, в которых эти производные не существуют, являются теми значениями независимых переменных, при которых функция может достигать экстремума. Эти точки называются критическими для функции .  Если дифференцируемая функция не имеет критических точек, то она и не имеет экстремума.

        Приведённая выше теорема не является достаточной для исследования вопроса об экстремальных значениях функции. Так, например, функция  z = x² - y²  имеет производные ,  , которые обращаются в нуль при x =0 и y = 0.  Но эта функция при указанных значениях не имеет ни максимума, ни минимума.

        Установим достаточные условия экстремума функции двух переменных.

Теорема 2. Пусть в некоторой области, содержащей точку M₀ (x₀, y₀), функция f (х, у) имеет непрерывные частные   производные до третьего порядка включительно. Пусть, кроме того, точка M₀ (x₀, y₀) является критической для функции f (х, у), то есть 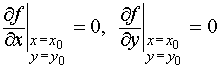 . Тогда при x = x₀, y = y₀:

1. f (х, у) имеет максимум, если 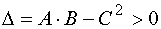  и A < 0,  где .

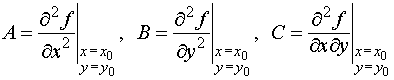2. f (х, у) имеет минимум, если   и A > 0.

3. f (х, у) не имеет ни максимума, ни минимума, если

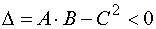
4. если 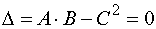 , то экстремум может быть, а может и не быть (в этом случае требуется дальнейшее исследование).

Замечание 1. Квадратичная форма   легко запоминается, если записать её в виде определителя:

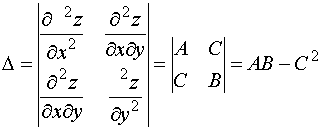.                              (1)

                            Если , в точке (x₀, y₀) есть экстремум.

                             Если  , экстремума нет.

Замечание 2.  В каждой точке M₀ (x₀, y₀) экстремума градиент функции z  = f (х, у) обращается в нуль-вектор,  а производная в любом направлении

 равна нулю: (grad  f  )_M = 0,  .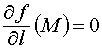

Замечание 3. В точке экстремума касательная плоскость к поверхности с уравнением  z  = f (х, у)  параллельна плоскости хоу.