43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен, а подынтегральная функция ограничена на нем — в противном случае множество сумм Дарбу не будет ограниченным. При решении задач встречаются случаи, когда одно или оба из этих условий не выполняются, т. е. когда промежуток интегрирования бесконечен или подынтегральная функция не ограничена. Такие интегралы называются несобственными. Различают несобственные интегралы 1-го и 2-го рода в зависимости от того, имеем ли мы дело с бесконечностью промежутка интегрирования или с неограниченностью подынтегральной функции.

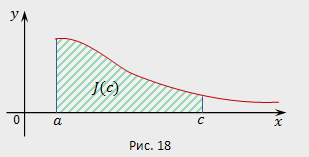
Хотя несобственные интегралы и нельзя рассматривать как разделяющие числа для сумм Дарбу, иногда им можно придать определенный смысл с помощью дополнительного предельного перехода. Начнем со случая, когда промежутком интегрирования является луч  . Предположим, что функция   интегрируема на каждой конечной части луча, т. е. что для любого  существует интеграл  . За значение интеграла   естественно принять предел функции  , когда с стремится к  , т. е. когда промежуток интегрирования стремится заполнить весь луч   (рис. 18).

Может, однако, случиться, что этот предел не существует. Поэтому будем различать два случая:

а) Если предел   существует и конечен, то несобственный   интеграл называют сходящимся, а значение этого предела — значением несобственного интеграла. В этом случае

(1)

б) Если предел в правой части равенства (1) не существует, говорят, что несобственный интеграл   расходится.

При аналогичных предположениях относительно функции   можно рассмотреть случай, когда верхний предел фиксирован, а нижний предел стремится к 

(2)

Если предел, стоящий в правой части равенства (2), конечен, то несобственный интеграл   называют сходящимся, в противном случае его называют расходящимся.

Наконец, можно определить и несобственный интеграл вида . Будем считать, что функция  интегрируема на всей числовой прямой  . Выберем на прямой произвольную точку  . Эта точка разобьет прямую   на два луча:  и  . Если существуют несобственные интегралы

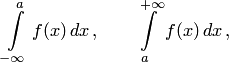
то говорят, что существует и несобственный интеграл  . В этом случае полагают

(3)

где несобственные интегралы, содержащиеся в правой части равенства (3), определены соответственно равенствами (1) и (2). Легко проверить, что значение интеграла не зависит от выбора точки  .

Пример 1. Вычислить несобственный интеграл   с бесконечным верхним пределом.

Решение. Подынтегральная функция   всюду непрерывна и, следовательно, интегрируема в любом конечном промежутке. Имеем:

Значит, окончательно имеем  .

44. Функции нескольких переменных, область определения.

1. Определение. Если каждой паре (x,y) значений двух независимых переменных из области Wставится определенное значение z, то говорят, что z есть функция двух переменных (x,y). 

   z=f(x,y)

2. Геометрическое изображение функции двух переменных - поверхность.

3. Частное и полное приращение функции.

Полное приращение функции 

Dz=f(x+Dx, y+Dy)-f(x,y)

Частное приращение функции 

Dx z=f(x+Dx)-f(x,y)

Dy z=f(x,y+Dy)-f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений.

Пример. z=xy. 

Dx z=(x+Dx)y-xy=yDx

Dy z=x(y+Dy)-xy=xDy

Dz=(x+Dx)(y+Dy)-xy=yDx+xDy+DyDx № Dy z+Dx z.

4. Непрерывность функции нескольких переменных

Предел функции.

Пусть z=f(x,y) определена в некоторой окрестности A(x₀,y₀).

Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству |AP| < d, имеет место неравенство |f(x,y)-b| < e.

5. Непрерывная функция

6. Частные производные

Если каждой совокупности значений "n" переменных

из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция

"n" переменных.

Множество D, указанное в определении 1.1, называется областью определяния илиобластью существования этой функции.

Если рассматривается функция двух переменных, то совокупности чисел

обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z = f ( x, y ) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.

Так, например, областью определения функции

является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению

т. е. представляет собой круг радиуса r с центром в начале координат.

Для функции

областью определения служат точки, которые удовлетворяют условию

т. е. внешние по отношению к заданному кругу.

Часто функции двух переменных задаются в неявном виде, т. е. как уравнение

связывающее три переменные величины. В этом случае каждую из величин x, y, z можно рассматривать как неявную функцию двух остальных.