41. Основные свойства определенного интеграла

Значение определенного интеграла не зависит от обозначения переменной интегрирования:  .

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: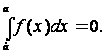 

Если  , то, по определению, полагаем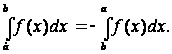 

Постоянный множитель можно выносить за знак определенного интеграла: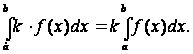 

Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

.

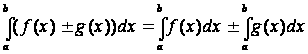Если функция   интегрируема на   и  , то

.

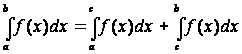(теорема о среднем). Если функция   непрерывна на отрезке  , то на этом отрезке существует точка  , такая, что .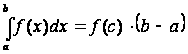

42. Вычисления определенного интеграла Формула Ньютона-Лейбница.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница:  .

Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.

Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.

Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента   интеграл вида   является функцией верхнего предела. Обозначим эту функцию  , причем эта функция непрерывная и справедливо равенство  .

Действительно, запишем приращение функции  , соответствующее приращению аргумента   и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства: 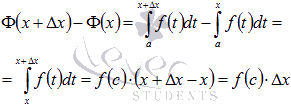  где  .

Перепишем это равенство в виде  . Если вспомнить определение производной функции и перейти к пределу при  , то получим  . То есть,   - это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как  , где С – произвольная постоянная.

Вычислим F(a), используя первое свойство определенного интеграла:  , следовательно,  . Воспользуемся этим результатом при вычислении F(b):  , то есть  . Это равенство дает доказываемую формулу Ньютона-Лейбница  .

Приращение функции принято обозначать как  . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид  .

Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразныхy=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрирования разобраны основные способы нахождения первообразной. Приведем несколько примеров вычисле

Замена переменной в определенном интеграле.

Пусть функция y = f(x) определена и непрерывна на отрезке [a; b]. Множество [a; b] является областью значений некоторой функции x = g(z), которая определена на интервале   и имеет на нем непрерывную производную, причем   и  , тогда  .

Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интегра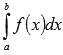л  , причем неопределенный интеграл   мы бы искали методом подстановки

Интегрирование по частям при вычислении определенного интеграла.

Пусть на отрезке [a; b] определены и непрерывны функции u(x) и v(x) вместе со своими производными первого порядка и функция   – интегрируема, тогда на этом отрезке интегрируема функция   и справедливо равенство  .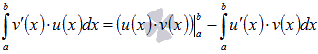

Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интеграл  , причем неопределенный интеграл   мы бы искали интегрированием по частям.