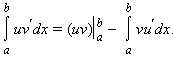- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
39. Геометрический смысл определенного интеграла
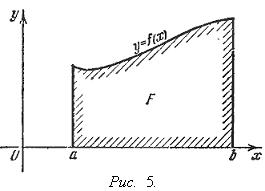
Если f(x) непрерывна и положительна на [a, b], то интеграл
![]()
![]()
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ..., zN. Составим для f(x) интегральную сумму σ.
Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в суммеσ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(zi) | (i = 1, 2, ..., N) есть K, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ,
откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл
существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так:
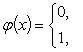

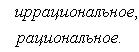
Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл
![]()
![]()
не существует.
В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
40. Формула Ньютона-Лейбница
Если
функция f ( x )
интегрируема на [ a ; b ],
то для любого
существует
интеграл
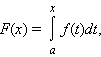 который
называется интегралом
с переменным верхним пределом .
который
называется интегралом
с переменным верхним пределом .
Если функция f интегрируема на [ a ; b ], то функция F ( x ) непрерывна на этом отрезке.
Если
функция f интегрируема
на [ a ; b ]
и непрерывна в ![]() то
функция F ( x )
дифференцируема в
причем
то
функция F ( x )
дифференцируема в
причем
![]()
Если
функция f непрерывна
на [ a ; b ],
то на этом отрезке она имеет
первообразную F вида
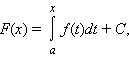 где C –
постоянная. Всякая первообразная
функции f на
отрезке [ a ; b ]
удовлетворяет этой формуле.
где C –
постоянная. Всякая первообразная
функции f на
отрезке [ a ; b ]
удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница :
Пусть
функция f ( x )
непрерывна на [ a ; b ],
а F ( x )
– какая-либо первообразная функции f на
этом отрезке. Тогда
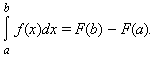
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f , вычислить ее значения в точках a и b и найти разность F ( b ) – F ( a ).
Пусть f ( x )
непрерывна на [ a ; b ], g ( t )
имеет непрерывную производную на
[α; β], ![]() Тогда
если a = g (α), b = g (β),
то справедливаформула
замены переменной в определенном
интеграле :
Тогда
если a = g (α), b = g (β),
то справедливаформула
замены переменной в определенном
интеграле :
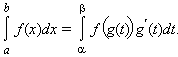
Если
функции u ( x )
и v ( x )
имеют на [ a ; b ]
непрерывные производные, то справедлива
формула интегрирования по частям: