33. Метод интегрирования подстановкой (заменой переменной)
Интегрирование
подстановкой ( замена переменной ). Если
функция f ( z )
определена и имеет первообразную
при z 
Z ,
а функция z = g ( x )
имеет непрерывную производную при x
X и
её область значенийg ( X ) Z ,
то функция F ( x )
= f [ g ( x )]
× g' ( x )
имеет первообразную на Х и
F ( x ) dx =
f [ g ( x )] • g' ( x ) dx =
f ( z ) dz .
П р и м е р . |
Найти
интеграл: |
Р е ш е н и е. |
Чтобы
избавиться от квадратного корня,
положим |
.
,тогда
x
= u2 +
3 и, следовательно, dx
= 2u
du.
Делая подстановку, имеем:
34. Метод интегрирования по частям
Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.
Пусть 
—
функции, дифференцируемые на некотором
промежутке 
.
Тогда, как известно, дифференциал
произведения этих функций вычисляется
по формуле
Взяв неопределенный интеграл от обеих частей этого равенства, получим:
Так
как 
,
а 
,
то
получаем: 
,
откуда 
.
Поскольку 
уже
содержит произвольную постоянную, в
правой части полученного равенства 
можно
опустить и записать равенство в виде
(1) |
Полученная формула называется формулой интегрирования по частям.
При
выводе формулы (1) мы предположили, что
функции 
и 
дифференцируемы.
Этой формулой обычно пользуются в тех
случаях, когда подынтегральное
выражение 
проще,
чем подынтегральное выражение 
.
Заметим, что одно и то же подынтегральное выражение можно различными способами записать в виде . Например,
и
т. д. Поэтому иногда приходится испытывать
различные формы такой записи, прежде
чем метод приведет к успеху. Обычно
стараются подынтегральное выражение
разбить на части 
и 
так,
чтобы вид 
был
не сложнее, чем вид 
,
а вид 
проще,
чем вид
.
В частности, полезно иметь в виду, что
для таких функций, как 
,
производные имеют вид более простой,
чем сами функции. Поэтому в большинстве
случаев эти функции удобно принимать
за функцию
.
Пример
1. Вычислим
по частям неопределенный интеграл 
.
Решение. Положим 
.
Тогда 
.
Используя формулу интегрирования по частям (1), получаем:
35. Понятия о рациональных функциях
36. Интегрирование простейших рациональных дробей
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены.
Рациональная дробь называется правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
I. 
;
II.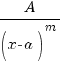 
,
где m - целое число, большее единицы;
III. 
,
где 
,
т.е квадратный трехчлен 
не
имеет действительных корней
IV.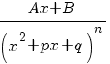 
,
где n - целое число, большее единицы, и
квадратный трехчлен
не
имеет действительных корней
Во всех четырех случаях предполагается, что A, B, p, q, a - действительные числа. Перечисленные дроби будем соответственно называть простейшими дробями I, II, III, IV типов.
Расмотрим интегралы от простейших дробей первых трех типов. Имеем
I. 
;
II.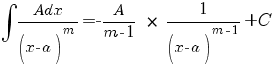 
III.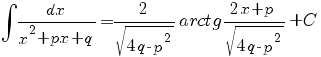 
Действительно, для этого частного случая простейшей дроби типа III получаем
,
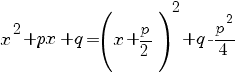или 
,
где 
,
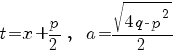откуда
