29. Понятие неопределенного интеграла

Выражение вида   называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.

Определение. Неопределенным интегралом  называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.  или  Функцию   называют первообразной функции   . Первообразная функции   определяется с точностью до постоянной величины.

Напомним, что   -дифференциал функции   и определяется следующим образом:

Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.

Например, известно, что   , тогда получается, что   , здесь   - произвольная постоянная.

Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы снеопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях. 

30.Свойства неопределенного интеграла

Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если         , то 

        Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению 

        Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы 

        Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов 

        Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов 

        Свойство 6. Постоянный множитель можно выносить за знак интеграла 

        Свойство 7. Если 

то 

31. Таблица основных неопределенных интегралов

Вычисление (взятие) интегралов заключается в том, чтобы специальными методами (заменами переменных) свести данный неопределенный интеграл к уже известному (существующему) интегралу, т.е. неопределенному интегралу из данной таблицы интегралов.

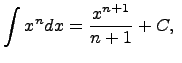1.    где

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

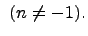
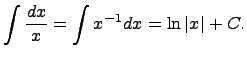
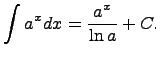
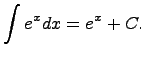
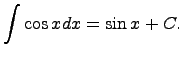
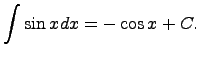
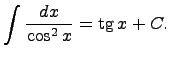
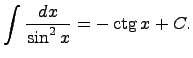
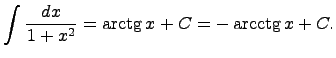
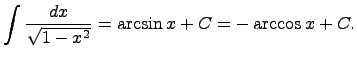
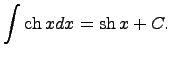
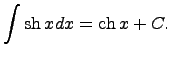
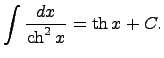
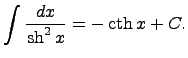
Здесь C - произвольная постоянная, т.к. производная от постоянной есть нуль, следовательно,неопределенный интеграл определяется с точностью до постоянной. 

32. Метод непосредственного интегрирования

Непосредственное интегрирование– интегрирование с использованием таблицы неопределенных интегралов, основных свойств и тождественных преобразований подынтегральной функции

Пример 1. Сначала приведем полное решение:

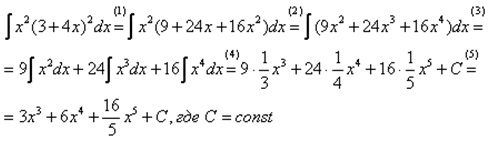
Комментарии:

(1) Используем формулу квадрата суммы  , избавляясь от степени.

(2) Вносим   в скобку, избавляясь от произведения.

(3) Используем свойства линейности интеграла (оба правила сразу).

(4) Превращаем интегралы по табличной формуле  .

(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь   – она несократима и в ответ входит именно в таком виде. Не нужно делить на калькуляторе  ! Не нужно представлять ее в виде  !

Пример 2. Найти неопределенный интеграл  .

Используя свойство неопределенного интеграла, вынесем за знак интеграла постоянную 2. Затем, выполняя элементарные математические преобразования, приведем подынтегральную функцию к степенному виду:

.

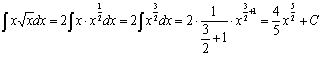Пример 3.