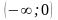- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
27. Выпуклость графика функции. Точки перегиба
Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
|
|
|
График 3.2.3.1. Выпуклая вверх функция |
Аналогично определяется функция, выпуклая вниз.
Дважды
дифференцируемая на [a; b] функция f (x) выпукла
вверх, если для любого ![]()
|
Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
|
Так,
вторая производная функции ![]() равна
равна ![]() откуда
следует, что квадратичная функция
выпукла вниз на всей области определения.
откуда
следует, что квадратичная функция
выпукла вниз на всей области определения.
Пусть
функция f (x) непрерывна
в точке ![]() и
имеет в этой точке конечную или бесконечную
производную. Тогда точка
называется точкой
перегиба функции f,
если в этой точке изменяется направление
ее выпуклости.
и
имеет в этой точке конечную или бесконечную
производную. Тогда точка
называется точкой
перегиба функции f,
если в этой точке изменяется направление
ее выпуклости.
Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x)имеет вторую производную, непрерывную в этой точке, то
|
Достаточные условия наличия точки перегиба.
Пусть
функция f (x) непрерывна
и имеет конечную или бесконечную
производную в точке ![]() Если
Если ![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку ![]() то
–
точка перегиба функции f (x).
то
–
точка перегиба функции f (x).
Если ![]()
![]() то
–
точка перегиба функции f (x).
то
–
точка перегиба функции f (x).
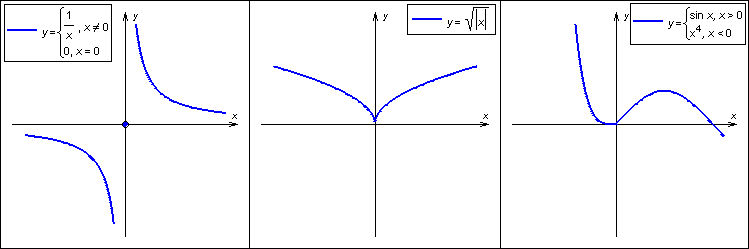
В заключение приведем примеры, когда точка x0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
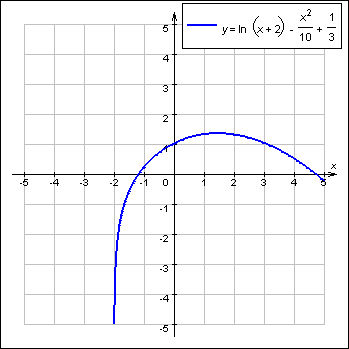
если функция разрывна в точке (например
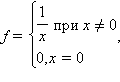
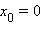 );
);в случае угловой точки (например,
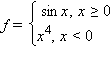
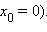
Не
являются точками перегиба и точки
возврата,
например точка ![]() у
функции
у
функции ![]()
Все вышеперечисленные случаи изображены на рисунке.
|
28.Общая схема исследования функции и построения графика
При построении графиков функций более сложного вида можно примерно придерживаться следующего плана:
1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.
2. Выяснить, является ли функция четной или нечетной.
3. Выяснить, является ли функция периодической.
4. Найти точки пересечения графика с осями координат (нули функции).
5. Найти асимптоты графика.
6. Вычислить производную функции f'(x) и определить критические точки.
7. Найти промежутки монотонности функции.
8. Определить экстремумы функции f(x).
9. Вычислить вторую производную f''(x).
10. Определить направление выпуклости графика и точки перегиба.
11. Построить график, используя полученные результаты исследования.
Следует иметь в виду, что при построении графика функции можно не всегда следовать указанному плану. Например, не всегда можно найти нули функции, даже если они существуют. Для построения графиков функций в ряде случаев пункты 9 и 10 можно пропустить.
Иногда для более точного построения дополнительно находят координаты некоторых точек графика.
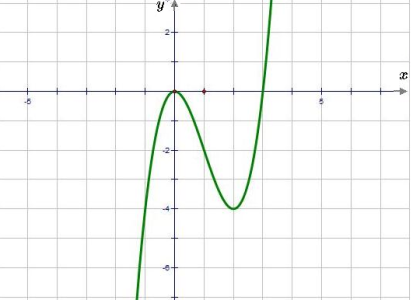
Пример. Исследовать функцию f (x) = x3–3x2 и построить ее график.
Решение:
1. Область определения функции - вся числовая ось.
2. Функция f (x) = x3–3x2 непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
f(–x) = (–x)3–3(–x)2 = –(x3+3x2) ≠ f(x) и f(–x) = (–x)3–3(–x)2 = –(x3+3x2) ≠ –f(x)
Функция не является ни четной, ни нечетной. Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, x3–3x2=0, x2(x–3)=0 ⇒ x=0, x=3. Значит (0;0), (3;0) - точки пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
y'=0 ⇒ 3x2–6x =0 ⇒ 3x(x–2) = 0 ⇒ x = 0, x = 2 - критические точки.
Промежутки монотонности, где функция возрастает или убывает, показаны в таблице стрелками. Экстремумы функции занесены в таблицу.
x |
|
0 |
|
2 |
|
f '(x) |
+ |
0 |
– |
0 |
+ |
f (x) |
↑ |
fmax(0)=0 |
↓ |
fmin(2)=–4 |
↑ |
7*. Вычисление второй производной: y''=0, 6x–6 = 0, x = 1.
8*. Промежутки выпуклости и точки перегиба: Направление выпуклости графика и точки перегиба занесены в таблицу.
x |
|
1 |
|
f '(x) |
– |
0 |
+ |
f (x) |
Выпукла вверх |
Точка перегиба y = –2 |
Выпукла вниз |
(Пункты 7* и 8* не являются обязательными).
9. Найдем значение функции в дополнительной точке: f(–1) = (–1)3– 3(–1)2 = –1–3 = –4.
10. Искомый график функции.