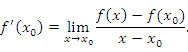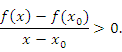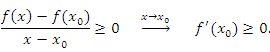- •1.Множества. Основные понятия. Операции над множествами
- •2.Числовые множества
- •3.Числовые промежутки. Понятие окрестности точки.
- •4.Понятие функции. Способы задания функции. Основные характеристики функции
- •5.Обратная функция. Сложная функция
- •6. Числовая последовательность. Предел числовой последовательности
- •7.Теоремы о предельных переходах в неравенствах.
- •8.Предел монотонной неограниченной последовательности. Теорема Вейерштрасса.
- •9. Предел функции в точке. Односторонние пределы.
- •16.2. Односторонние пределы
- •10. Бесконечно малые функции: определение и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •11.Связь между функцией, ее пределом и бесконечно малой функцией.
- •12.Основные теоремы о пределах
- •13. Признаки существования пределов. Теоремы о пределе промежуточной функции и о пределе монотонной функции.
- •14. Первый замечательный предел
- •15. Второй замечательный предел
- •16. Непрерывность функции в точке, в интервале, на отрезке.
- •17. Точки разрыва функции и их классификация.
- •18.Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •Непрерывность элементарных функций
- •19.Свойства функций, непрерывных на отрезке.
- •20.Определение производной, ее геометрический и экономический смысл.
- •21. Связь между непрерывностью и дифференцируемостью функций.
- •22. Производные суммы, разности, произведения и частного
- •23.Производные сложной функции
- •24.Производные основных элементарных функций
- •25. Возрастание и убывание функций
- •26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
- •27. Выпуклость графика функции. Точки перегиба
- •28.Общая схема исследования функции и построения графика
- •29. Понятие неопределенного интеграла
- •30.Свойства неопределенного интеграла
- •31. Таблица основных неопределенных интегралов
- •32. Метод непосредственного интегрирования
- •33. Метод интегрирования подстановкой (заменой переменной)
- •34. Метод интегрирования по частям
- •35. Понятия о рациональных функциях
- •36. Интегрирование простейших рациональных дробей
- •37. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка
- •38. Определенный интеграл как предел интегральной суммы
- •39. Геометрический смысл определенного интеграла
- •40. Формула Ньютона-Лейбница
- •41. Основные свойства определенного интеграла
- •42. Вычисления определенного интеграла Формула Ньютона-Лейбница.
- •Замена переменной в определенном интеграле.
- •Интегрирование по частям при вычислении определенного интеграла.
- •43. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования(несобственный интеграл I рода). Интеграл от разрывной функции (несобственный интеграл II рода)
- •44. Функции нескольких переменных, область определения.
- •45. Производные и дифференциалы функций нескольких переменных.
- •46. Экстремум функций многих переменных.
- •47. Условный экстремум. Метод множителей Лагранжа.
24.Производные основных элементарных функций
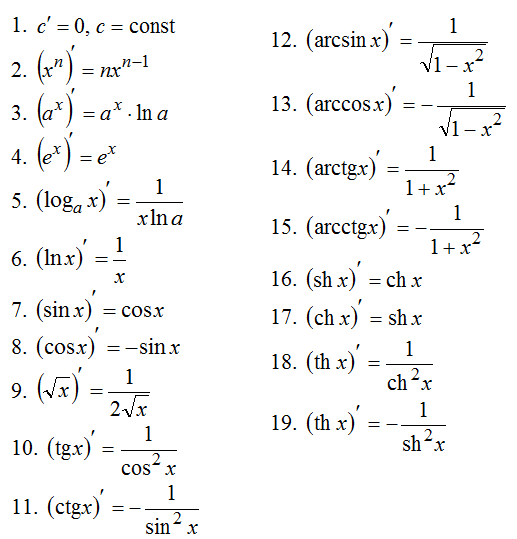
25. Возрастание и убывание функций
Функция
влечет за собой неравенство
Функция называется возрастающей на интервале , если
Другими словами, большему значению аргумента соответствует большее значение функции. Аналогично вводятся понятия невозрастающей функции и убывающей функции. Функция называется невозрастающей на интервале , если
Функция называется убывающей на интервале , если
(Большему
значению аргумента соответствует
меньшее значение убывающей
функции).
Имеется
тесная взаимосвязь между поведением
функции
в некотором промежутке и знаком
производной
Если
Тогда
и, следовательно, функция является возрастающей в окрестности точки . Предположим теперь, что функция является неубывающей в окрестности точки . Тогда
Аналогично устанавливается, что условие
является необходимым и достаточным для того, чтобы функция была невозрастающей в окрестности точки .
|
26. Максимум и минимум функций. Необходимое и достаточное условие экстремума
Говорят,
что функция f (х)
имеет в точке ![]() максимум (минимум),
если существует такая окрестность
максимум (минимум),
если существует такая окрестность ![]() точки
,
что для всехиз этой окрестности, отличных
от
,
выполняется неравенство
точки
,
что для всехиз этой окрестности, отличных
от
,
выполняется неравенство
![]() (соответственно
(соответственно ![]() ).
Иначе
говоря, функция f (х)
имеет в точке
максимум
(минимум), если для достаточно малого
приращения Δх (любого
знака) выполняется неравенство
).
Иначе
говоря, функция f (х)
имеет в точке
максимум
(минимум), если для достаточно малого
приращения Δх (любого
знака) выполняется неравенство ![]() (
(![]() ).
).
Максимум и минимум функции называются экстремумом функции. По определению, максимум и минимум функции могут достигаться лишь внутри области определения, а концы отрезков области определения, не могут служить точками, в которых функция принимает экстремум.
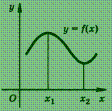
На
рис. изображен график функции, которая
имеет в точке ![]() максимум,
а в точке
—
минимум.
максимум,
а в точке
—
минимум.
 Теорема
1 (необходимое
условие существования экстремума).
Теорема
1 (необходимое
условие существования экстремума).
Если
функция f (х),
дифференцируемая в интервале (а ; b),
имеет в точке
, ![]() ,
экстремум, то ее производная в этой
точке равна нулю:
,
экстремум, то ее производная в этой
точке равна нулю: ![]() (1)
Условие (1), будучи необходимым условием
экстремума, не является достаточным
условием экстремума, что показывает
следующий пример.
(1)
Условие (1), будучи необходимым условием
экстремума, не является достаточным
условием экстремума, что показывает
следующий пример.
Пример 1.
Функция ![]() не
имеет экстремума в точке
не
имеет экстремума в точке ![]() (разность
(разность ![]() меняет
знак при изменении знака аргумента х),
хотя ее производная
меняет
знак при изменении знака аргумента х),
хотя ее производная ![]() обращается
в этой точке в нуль.
Теорема
2 (первое
достаточное условие существования
экстремума).
обращается
в этой точке в нуль.
Теорема
2 (первое
достаточное условие существования
экстремума).
Если производная функции f (х) обращается в точке в нуль (такие точки называются критическими) и при переходе через эту точку в направлении возрастания х меняет знак с «плюса» («минуса») на «минус» («плюс»), то в точке функция имеет максимум (минимум).
Если же при переходе через точку производная функции f (х) не меняет знака, то в этой точке функция f (х) экстремума не имеет.
Отсюда следует правило исследования функции на экстремум с помощью первой производной.
Пусть в интервале (а ; b) дана дифференцируемая функция f (х).
Тогда для исследования ее на экстремум: 1) находят производную f ′ (х); 2) находят корни уравнения f ′ (х) = 0; 3) выясняют знак f ′ (х) слева и справа от каждого из этих корней и согласно теореме 2 делают заключение об экстремуме; 4) вычисляют значения функций в точках экстремума.
Пример 2.
Исследуем на экстремум функцию ![]() .
Вычисляем производную
.
Вычисляем производную
![]() и
находим корни уравнения
и
находим корни уравнения
![]()
Имеем
![]() .
.