20.Определение производной, ее геометрический и экономический смысл.

Рассмотрим функцию f(x), область определения которой содержит некоторый открытый интервал вокруг точки x0. Тогда функция f(x) является дифференцируемой в точке x0, и ее производная определяется формулой Для производной используются обозначения: Для нахождения производной функции f(x) в точке x0 на основе определения следует выполнить следующие действия: Записать отношение  ; Упростить дробь, сократив ее, если возможно, на Δx; Найти производную  , вычисляя предел дроби. Если данный предел существует, то говорят, что функция  f(x) дифференцируема в точке x = x0.

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

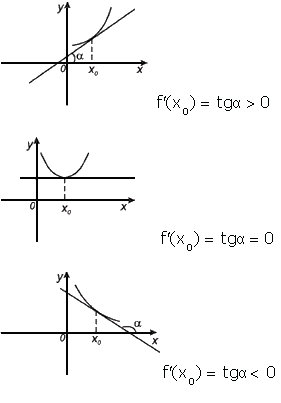
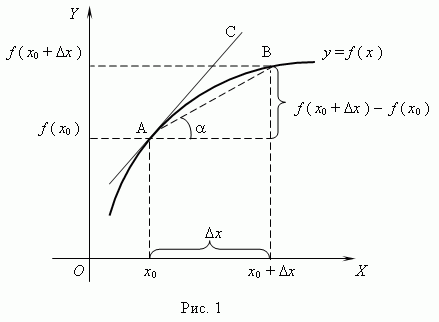
Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

Экономический смысл производной

Производительность труда есть производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной.

Пусть y(x) — функция, характеризующая, например, издержки производства, где x — количество выпускаемой продукции. Тогда отношение  описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского «average».) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением  . Производная   выражает предельные (маргинальные от английского «marginal») издержки производства. Величину Mf(x) = y' называют мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определить предельную выручку, предельный доход, предельную полезность и другие предельные величины.

Определение. Отношение   называется темпом прироста функции y. Отношение   называется мгновенным темпом прироста.

Обычно степень влияния одной переменной на другую, зависимую от нее, измеряют производной данной функции. Однако часто экономистов интересуют относительные изменения величин. Например, если маленькое яблоко подорожало на 2,5 рубля, то при этом большое, скажем, на 5. В тоже время, если яблоки подорожали в 1,5 раза, то в 1,5 раза дороже стало и маленькое, и большое яблоко, и килограмм, и вагон яблок. Поэтому дляанализа относительных изменений вместе с понятием производной используют понятие эластичности.

Определение (эластичность). Эластичностью функции Ex(y) называется величина   Будем говорить, что y(x) эластична в точке x, если | Ex(y) | > 1, y(x) неэластична, если | Ex(y) | < 1, и нейтральна, если | Ex(y) | = 1.

Рассмотрим некоторые свойства эластичности.

• Эластичность — безразмерная величина, ее значение не зависит от того, в каких единицах измерены аргумент и функция. Если u = Ax, v = By, то  ;

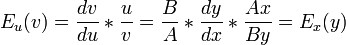• Эластичности взаимно обратных функций — взаимно обратные величины

• Эластичность функции равна произведению независимой переменной x на темп изменения функции 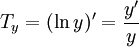 , то есть E_x(y) = xT_y.

• Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций:

E_x(uv) = E_x(u) + E_x(v), .

• Из последнего свойства следуют формулы

E_x(xy) = E_x(x) + E_x(y) = 1 + E_x(y) отсюда, если E_x(y) > − 1, то xy монотонно возрастает; если E_x(y) < − 1, то xy монотонно убывает. Аналогично,