Прямоугольник, Параллелепипед и Цилиндр, а так же изображение Перспективы
В этом разделе мы сосредоточимся на перспективе. Поскольку я рассказываю о перспективе применительно к рисованию персонажей, а не технических чертежей и т.д., то я не буду давать математического определения и описания понятия "перспектива". Речь пойдет об основных моментах использования перспективы в рисунках, для того чтобы Вы поняли, что это такое и как этим пользоваться. Итак, что такое перспектива? Перспектива - это средство отобразить глубину рисунка. Простой пример: представим себе железную дорогу. Все знают, что рельсы лежатпараллельно, а это значит, что они нигде не пересекаются.
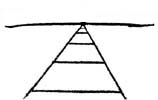
Однако, если вы встанете на пути и посмотрите вдаль (Прим. перев.: я бы не рекомендовал это делать. Может выйти боком. А если точнее, то буфером. :)), то будет казаться, что с удалением от вас, рельсы сходятся ближе, пока, наконец, не сольются в одну точку. То же самое можно увидеть, если выйти на прямой участок обычной дороги. Только здесь вместо рельс будут сходиться края дороги. Точку, где рельсы или края дороги соединяются, называют "точкой схода" (vanishing point). Эта точка всегда лежит на линии горизонта. Почему так? Иначе рельсы уходили бы в небо или обрывались бы, не достигая горизонта.
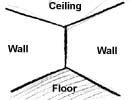
Давайте посмотрим в угол комнаты. Можно заметить, что потолок и пол ближе друг к другу в углу, чем в том месте, где вы сидите. Это основополагающий принцип перспективы. Чем дальше объекты от наблюдателя, тем они меньше и ближе друг к другу.
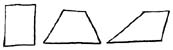
Перспектива может применяться как ко всем объектам на рисунке, так и к одному единственному. Возьмем для примера прямоугольник. Он состоит из 4 линий: верхней, нижней и двух боковых. Каждую линию можно изобразить в перспективе. Нарисуем прямоугольник, у которого верхняя сторона короче нижней. Сначала нижнюю линию, потом верхнюю. Теперь боковые линии. Кажется, что прямоугольник не лежит на листе, а уходит вглубь него. Нарисуем еще один прямоугольник, но сместим верхнюю и нижнюю линии в противоположные стороны. Впечатление похожее на предыдущее, но в этом случае кажется, что он "скошен" или уходит в глубину под углом. Обратите внимание, как легко рисуются боковые линии. Для этого нужно просто соединить отрезками вершины верхней и нижней линий. Это важный момент при рисовании перспективы.
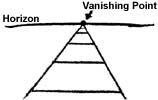
В предыдущем примере мы не использовали точку схода. Давайте попробуем проделать следующее упражнение с рельсами, с использованием этой точки. Нарисуем прямую линию поперек листа бумаги. Это будет наша линия горизонта. Теперь поставим где-нибудь на ней точку. Это будет точка схода. Проведем две прямые, уходящие в горизонт и оканчивающиеся в этой точке. Если Вам трудно просто так провести прямую линию, возьмите линейку. Прямые должны сближаться к точке схода. При желании можно нарисовать шпалы, делая их ближе друг к другу по мере приближения к точке схода. Обратите внимание, что, меняя местоположение точки схода, можно добиться смены направления рельс. Таким образом, контролируется перспектива объекта.
Попробуем нарисовать то же самое, но на этот раз вместо рельс возьмем сетку. Это поможет понять, что расстояние между "квадратами" сетки должно изменяться пропорционально. С помощью линейки нарисуем вертикальные линии сетки, выходящие из точки схода. Так же нарисуем горизонтальные линии сетки, причем они должны располагаться ближе друг к другу по мере приближения к горизонту. Есть и более точные способы отображения расстояний между горизонтальными линиями, но об этом как-нибудь потом.
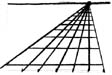
Это было введение в понятие перспективы. Теперь рассмотрим, как применить наши знания к конкретным объектам.
Начнем с простых фигур. Прямоугольник, куб (или параллелепипед) и цилиндр. Квадрат - это совсем просто и я не буду заострять на нем внимание. Куб (параллелепипед) - это трехмерный прямоугольник (как сфера - это трехмерная окружность). Цилиндр - это что-то среднее между сферой и параллелепипедом.
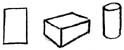
Если параллелепипед это трехмерный прямоугольник, то куб - это параллелепипед с одинаковыми сторонами. Он имеет шесть сторон или поверхностей, но в жизни мы можем увидеть только три из них. Если посмотреть на параллелепипед спереди, сверху или сбоку, мы увидим прямоугольник. Чтобы нарисовать параллелепипед под углом, нам придется использовать перспективу. Я надеюсь, вы внимательно изучили предыдущие уроки? Если Вы найдете настоящий параллелепипед, то это нам очень поможет в дальнейшем. Возьмите обычный спичечный коробок или что-нибудь похожее. Изучите его внимательно. Убедитесь, что с какой бы стороны Вы не взглянули на коробок, невозможно одновременно увидеть более трех сторон. Разверните его так, чтобы были видны только две стороны. Посмотрите на него сбоку - Вы сможете увидеть только одну сторону.
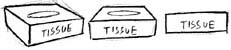
Как Вы видите, каждая видимая плоскость имеет 4 стороны, как у прямоугольника. Однако стороны не параллельны, они располагаются под углом друг к другу. Если приглядеться повнимательнее, то можно заметить, что с удалением от Вас стороны сужаются (эффект перспективы). Теперь нарисуем параллелепипед на бумаге. Для начала нарисуем его под таким углом зрения, чтобы видимыми были только две стороны. На рисунке я немного преувеличу перспективу для улучшения восприятия. Положите коробок перед собой так, чтобы видеть переднюю и верхнюю стороны. Начнем рисование с передней стороны. На первый взгляд она выглядит как обычный прямоугольник, но если Вы присмотритесь повнимательнее, то увидите, что нижняя линия чуть короче верхней. Это происходит потому, что нижняя часть находится от вас немного дальше, чем верхняя.
Теперь нарисуем верхнюю сторону (плоскость). Ее передняя грань уже нарисована, так как она одновременно является верхней гранью передней плоскости. Нарисуем вторую грань верхней плоскости параллельно первой, но немного короче. Обратите внимание, что эта грань намного меньше нижней грани передней плоскости. Опять же, это происходит потому, что она расположена еще дальше этой грани. Теперь дорисуем оставшиеся линии.
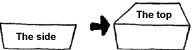
Взглянем на рисунок и проанализируем изображение. Объекты, расположенные дальше уменьшаются в размере и так же уменьшается расстояние между ними. Именно это и происходит с параллелепипедом. Несмотря на его небольшие размеры, мы все равно видим перспективу. На этой картинке мы применили то, что называется "2-х точечной перспективой". Отличие от "1-точечной перспективы" в том, что в первой используются две точки схода, а во второй - только одна (вспомните железную дорогу!). Вы можете мысленно представить, где находятся обе точки схода на рисунке параллелепипеда. Можно нарисовать эти точки вначале и использовать их как вспомогательное средство при рисовании перспективы. Единственное, чего не стоит делать - это располагать две точки слишком близко друг от друга. Это приведет к неправдоподобно большой перспективе и конечный рисунок будет выглядеть криво.
Теперь нарисуем параллелепипед под другим углом. Это будет посложнее предыдущих упражнений. Мы будем использовать "3-х точечную перспективу", что означает присутствие трех точек схода. Так же это значит, что вы увидите сразу три стороны параллелепипеда. Для этого упражнения придется нарисовать эти три точки схода в отличие от прошлого раза, где мы рисовали их мысленно. Разверните спичечный коробок так, чтобы были видны три стороны, как показано на одном из рисунков выше. Один из углов должен быть ближе остальных. Перед началом рисования, попробуем прикинуть, где должны располагаться три точки схода. С непривычки это покажется трудно и чтобы облегчить задачу, думайте о каждой точке как об отдельной точке для конкретной поверхности (как в 1-точечной перспективе). Ниже приведен рисунок с примером расположения трех точек схода.
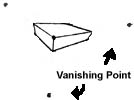
Начнем рисование с размещения трех точек схода как показано на следующей картинке. Теперь надо отметить точку ближайшего к вам угла параллелепипеда. Она должна располагаться между точками схода. Далее, с помощью линейки соединим точку угла с точками схода. Мы обозначили местоположение трех граней параллелепипеда.
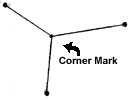
Теперь определимся с поверхностями нашего паралелепипеда. Отметим на правой прямой отрезок, обозначающий самую длинную грань. Сделаем то же самое на прямой слева. Это будет ширина. Наконец отметим высоту параллелепипеда.
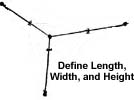
С помощью линейки соединим новые точки с точками схода. Не перепутайте, что с чем нужно соединить. Должна получиться картинка, похожая на ту, что вы видите внизу. Из каждой точки схода должно выходить по три линии.
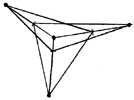
А теперь, если взглянуть повнимательнее, то можно увидеть, что наш параллелепипед практически нарисован. Все что осталось - это обвести нужные линии и рисунок готов.
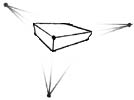
Я рекомендую повторять это упражнение до тех пор, пока не научитесь рисовать параллелепипед с закрытыми глазами. Поизменяйте местоположение точек схода и расстояния между ними. Вы заметите, что чем ближе точки друг к другу, тем более выражена перспектива (в моем примере я ее чуть преувеличил). Посмотрите, что будет, если переместить точку ближайшего угла. А что будет, если вынести ее наружу? Поизучайте изменение сторон. В итоге Вы должны научиться быстро рисовать параллелепипед без использования точек схода. Хотя, если Вы создаете реальный рисунок, то для правильного отображения объектов, их использование не возбраняется. Взгляните на следующие объекты и прикиньте, где должны располагаться точки схода для каждого из них. Не спешите, попрактикуйтесь, а когда почувствуете себя готовым, читайте дальше.
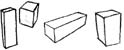
Последняя фигура - это цилиндр. Цилиндр выглядит круглым, если смотреть на него сверху, и прямоугольным, если смотреть сбоку (предполагается, что цилиндр стоит вертикально). Банка газировки - это цилиндр. Ствол дерева - тоже цилиндр. Ваша рука - это набор цилиндров, так же как и Ваши пальцы. Цилиндр не имеет углов, но имеет грани. Это что-то среднее между сферой и параллелепипедом.
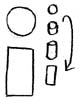
Рисовать цилиндр довольно просто, а изображение его перспективы похоже на перспективу параллелепипеда. Разница заключается в том, что количество сторон у него поменьше и окончание представляет собой окружность. Просто рисуем две параллельные линии и окружность (либо что-нибудь другое, что зависит от формы цилиндра). Рисование в перспективе немного труднее. Я не буду вдаваться в подробности рисования цилиндра под углом. Единственное, о чем нужно помнить, это то, что окончание цилиндра должно рисоваться в перспективе. Это значит, что торец цилиндра будет выглядеть как эллипс (плоская окружность). При рисовании цилиндра важно сохранять углы. Если угол перпендикулярный (90 градусов), то он должен остаться таким и в перспективе.
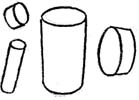
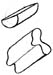
Еще одним важным моментом является соблюдение параллельности сторон цилиндра (если это необходимо). Ниже приведены несколько объектов сложной формы. Вы можете нарисовать похожую форму на обоих концах объекта, а затем соединить их линиями.
Хорошая работа :) Мы закончили первый урок и узнали массу полезного. Во втором уроке мы, опираясь на уже полученные знания, будем создавать более сложные объекты, комбинируя их из простых. Комплексные Объекты
Добро пожаловать на Урок 2: Комплексные (составные) Объекты. Надеюсь, Вы внимательно прочитали и разобрали Урок 1, поскольку здесь мы будем использовать приемы, о которых было рассказано ранее.