23. Необходимое и достаточное условие экстремума функции 2-х переменных. Примеры.

Необх.усл.сущ.экстр.:Если ф-я z= f(x,y) имеет в т.М0(х0,у0)экстремум и в этой т. Сущ-т частные производные z’x и z’y, то f’x(x0,y0)=0, f’y(x0,y0)=0

Пр-р:z=x^3+y63, z’x=3x^2, z’y=3y^2. Произв-е равны нулю в т(0;0),ног экстр. Эта ф-я в т.(0,0) не имеет,т.к. в любой окрестности этой точки она принимает знач-я разных знаков,а в самой т(0;0)

Z=0

Пусть ф-ия f(x,y), непрерывная вместе со своими частными производными 1-го и 2-го порядков в некот-й окрестности т.М0(х0,у0),удовлетворяет усл-м

Пр-р:Исследовать на экстр-м ф-ю z=x^3+y^3-3xy.Ее частные производные z’x=3x^2-3y; z’y=3y^2-3x

Обращается в нуль в точках М0(0,0) и М1(1,1).Ее 2-е производные равны z’’x^2=6x , z’’xy=-3, z’’y^2=6y.В т.М0 имеем D=-9<0, след-но,экстр.в этой точке нет.В т.М1 имеем D=27>0,причем А=6 >0,след-но.в т.М1-мин.

24. Объем тела. Понятие 2-го интеграла. Простейший случай вычисления 2-го интеграла. Примеры.

Как и для функций одной переменной y=f(x) вводится понятие двойного интеграла, т.е. определенный интеграл функции двух переменных z=f(x,y) по некоторой области Q. Известен геометрический смысл определенного интеграла функции одной переменной – это площадь криволинейной трапеции, аналогично смысл и двойного интеграла – это объем тела, основанием которой является область Q, а сверху ограничена поверхностью z=f(x,y) , это тело называется цилиндроид.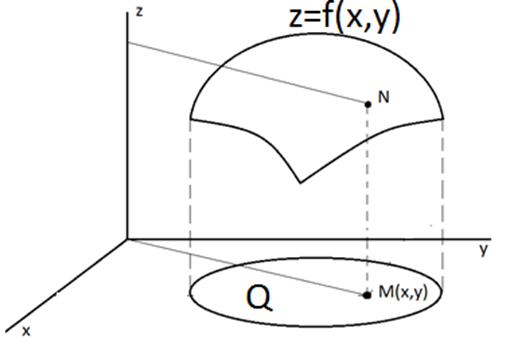

Вычисление 2-го интеграла зависит от обл-и Q. Вычисление двойного интеграла: 1) область Q является прямоугольник со сторонами a<=x<=b, c<=y<=d

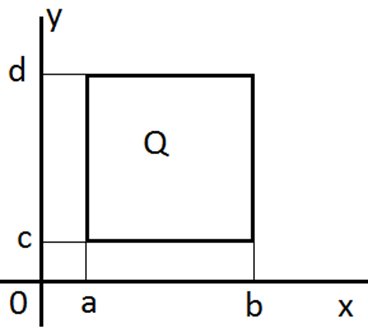В этом случае интеграл записывается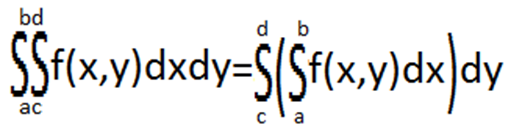

Различные случаи выч-я фигур при помощи опр-го интеграла

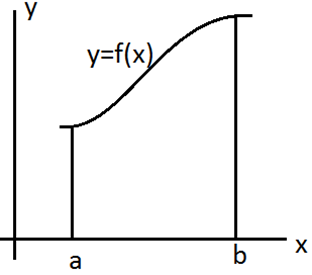С помощью определенного интеграла можно вычислить площадь криволинейных фигур. Криволинейной фигурой называется плоская фигура ограниченная графиками функций. Площадь вычисляется по формуле .
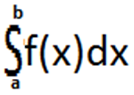