
- •11. Применение производной 2-го порядка для определения промежутков выпуклости и вогнутости графика , точки перегиба и вида экстремума.
- •16. Интегрирование простейших дробей и тригонометрических функций. Примеры.
- •21. Частные производные 1-го, 2-го порядка .
- •22. Касательная плоскость и нормаль к поверхности.
- •23. Необходимое и достаточное условие экстремума функции 2-х переменных. Примеры.
- •24. Объем тела. Понятие 2-го интеграла. Простейший случай вычисления 2-го интеграла. Примеры.
21. Частные производные 1-го, 2-го порядка .
Пусть
задана функция явно z=f(x,y). Введем понятие
частной производной. Так как функция
зависит от (x,y), то функцию можно
дифференцировать по переменной x и y,
соответственно их обозначают ся
 .
Последнее читается «дэ эф по дэ икс».
.
Последнее читается «дэ эф по дэ икс».
Введем определение одной производной, например Z’x. 1) для определения Z’x зафиксируем переменную y=const, получим Z=f(x,c). Тогда имеем функцию одной переменной. А для функции одной переменной понятие производной известно. 2) для х дадим превращение , получим значение . Вычислим значение при х и , т.е. f(x,c) и f( ,c). 3) вычислим превращение функции , . Значок «х» обозначает превращение по х. составим отношение превращений, вычислим предел при : . Если этот предел существует, то он называется частной производной по х, записывается: . Аналогично зафиксировав переменную х, мы получим понятие частной производной по y.
Частные производные второго порядка.
Как и для функций одной переменной y=f(x) для которой можно вычислить производные второго и третьего порядка, можно вычислить производные второго порядка для функций z=f(x,y). Это значит от вычисленной производной надо вычислить еще раз производную. Вторые частные производные обозначаются последнее читается «дэ дважды от z по дэ икс в квадрате». Очевидно, что от частных производных по x Z’x можно вычислить частную производную по y, обозначается Z’’xy. Также можно вычислить от частной производной Z’y производную по x – Z’’yx.
Дифференциал функции двух переменных вычисляется аналогично одной переменной. y=f(x) dy=f(x)dx. Тогда для функции двух переменных z=f(x,y) также надо вычислить частные производные f’x и f’y, а затем домножить первое на dx, а второе на dy, затем взять их сумму. Получим dz=f’xdx+d’ydy
22. Касательная плоскость и нормаль к поверхности.
В
трехмерном пространстве поверхности
задаются: 1) явными уравнениями z=f(x,y). В
этом случае график функций z=f(x,y) является
поверхностью. 2) неявное уравнение
F(x,y,z)=0, т.е. переменные x,y,z содержатся в
одной формуле. Часто трудно выразить z
через x,y. На поверхности заданной явно
или неявно можно определить линии
поверхности. Уравнения этой линии можно
задать следующим образом: 1) известно
что линии в пространстве в системе
координат Oxyz задается параметрическими
уравнениями
 , т.е. конец вектора из точки О описывает
некоторую линию, т.е. вектор имеет
переменные координаты
, т.е. конец вектора из точки О описывает
некоторую линию, т.е. вектор имеет
переменные координаты![]() . 2) чтобы эта линия лежала на поверхности
надо чтоб эти переменные
. 2) чтобы эта линия лежала на поверхности
надо чтоб эти переменные
 удавлетворяли уравнению поверхности.
Тогда получим уравнение линии лежащей
на поверхности
удавлетворяли уравнению поверхности.
Тогда получим уравнение линии лежащей
на поверхности![]() .
.
Чтобы
вести понятие нормаль и касательной,
надо продифференцировать уравнение
линии на поверхности. При этом уравнение
зависит от x,y,z которые зависят от t.
следовательно будем вычислять частные
производные по x,y,z и обыкновенные
производные по t. Воспользуемся правилом
производной сложной формы. Получим
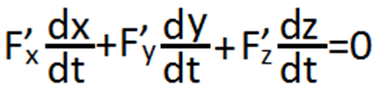 .
Это уравнение рассмотрим как скалярное
произведение двух векторов
.
Это уравнение рассмотрим как скалярное
произведение двух векторов
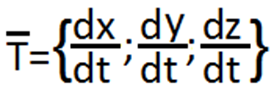 и
и
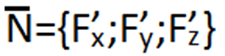 . Так как скалярное произведение равно
0, то векторы пермендикулярны. Известно
что вектор Т является касательной
кривой.
. Так как скалярное произведение равно
0, то векторы пермендикулярны. Известно
что вектор Т является касательной
кривой.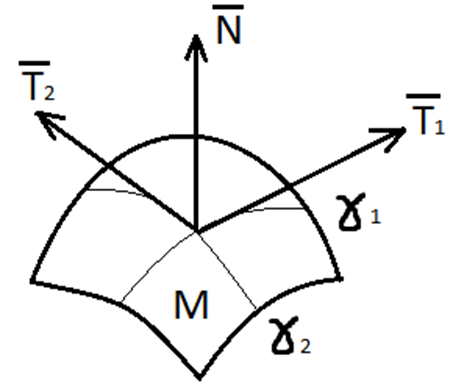 .
.
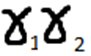 -линии поверхности. Векторы Т1Т2-касательные
векторы к линии. Вектор N нормальный
вектор(перпендикулярный). Перпендикулярные
векторы Т и N называется нормальным
вектором поверхности, а прямая проходящая
через этот вектор называется нормалью.
Уравнение нормали n запишем как уравнение
прямой в геометрии. Пусть M0(x0,y0,z0)-точка
поверхности, тогда вектор N нормали в
этой точке имеет координаты N0{F’x(x0,y0,z0),
F’y(x0,y0,z0), F’z(x0,y0,z0)}.
-линии поверхности. Векторы Т1Т2-касательные
векторы к линии. Вектор N нормальный
вектор(перпендикулярный). Перпендикулярные
векторы Т и N называется нормальным
вектором поверхности, а прямая проходящая
через этот вектор называется нормалью.
Уравнение нормали n запишем как уравнение
прямой в геометрии. Пусть M0(x0,y0,z0)-точка
поверхности, тогда вектор N нормали в
этой точке имеет координаты N0{F’x(x0,y0,z0),
F’y(x0,y0,z0), F’z(x0,y0,z0)}.
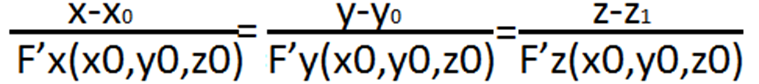 -каноническое уравнение прямой.
-каноническое уравнение прямой.
