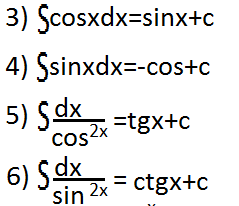1.Функция - это одно из важнейших математических понятий. Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция. Монотонность функции – это неубывание и невозрастание функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции. Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. Прямая к которой бесконечно близко приближается график какой-либо функции называется асимптотой. Область значений – это множество всех значений, которые может принимать переменная «игрек».

2.Последовательностью (аn)наз-ся мн-во дискретных знач-й ф-ий при натур-х знач-х аргумента.

число А называется пределом последовательности an при n стремящимся к бесконечности(+беск),если для любого номера n,большего номера N(n>N), для всех членов An и малого положительного числа E выполняется (an-A)<E,словами. все члены an последовательности с номерами n,большие числа N лежат от числа A на расстоянии, меньше E,то есть меньше an «сгущаются» около числа A.они могут «сгущаться» как слева, так и справа числа А или с обоих сторон.Свойства пределов: последовательности можно складывать,вычетать,умножать,делить, и произвести над ними математические действия(напр извлечь корень) тогда верны теоремы.

Послед-ти(an)наз-ся бесконечно малыми если их предел равен 0.

Пр-р: an=4\n,т.к. =

Величина,обратная бесконечно малой,наз-ся бесконечно большой.т.е.

тогда1/0=∞,1/∞=0

3.Пределы ф-й на беск-х 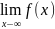опр-ся и выч-ся полн-ю анал-о пределам последов-й(вместо n исп-ся х)

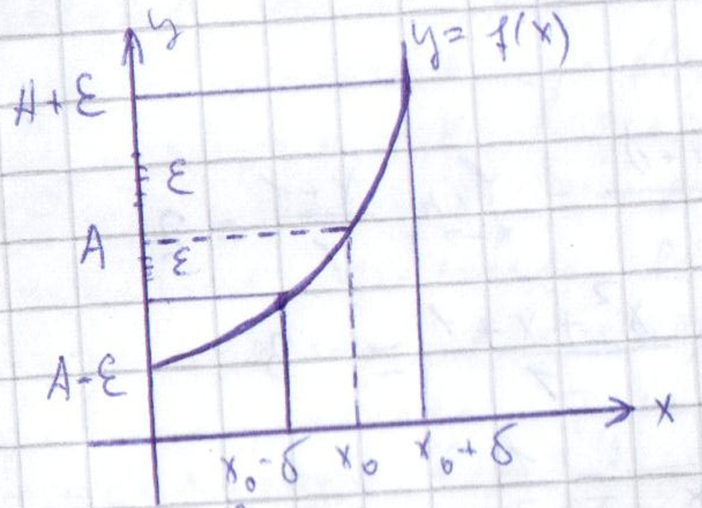
Число а наз-ся пределом ф-й у=f(x)в т.х0,если для любого малого пол-го числа υ и знач-й арг-а из окрест-й(х-υ,х+υ) зн-я ф-ий f(x)лежат от числаА на расст-и не больше Е,пол-го малого числа.т.е.(форм-й)из (х-х0)<υ,υ>0,след-т|f(x)-A|<E1E>0.Кратко,если зн-я арг-а х,”сгущ-ся”около числа х0,то зн-я ф-й у=f(x) сгущ-ся около числаА.

4. Замечательный предел 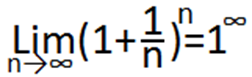-это неопределенность. Этот предел вычислил Неппер. =е=2,71828

Правила Лопиталя сформулирует неопределенности вида 1-4 от функции f(x) и g(x) равны пределам этих же функции.

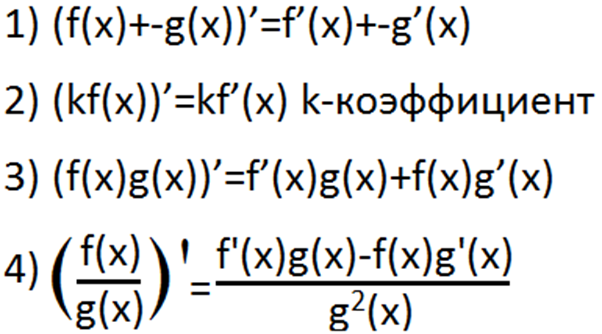
Пр-р: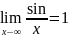

5.Пусть задана функция y=f(x). Непрерывная . Значение аргумента х дадим превращение dx(дельта икс), получим новое значение x+dx. В точках X и x+dx вычислим значение функции . Разность между этими значениями f(x+dx)-f(x)=dy называется превращением функции. Составим отношение , тогда предел 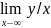.Если он сущ-т,то он наз-ся производной ф-ии у=f(x)

К понятию произ-й приводит задача выч-ия мгновенной ск-ти неравномерного дв-я.при этом исп-ся понятие ф-ий в точке.Если за время t тело прошло путь S,то ср.ск.υсрv= .

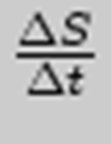Формула ск-ти не хар-т хар-р движ-я в какой-то мом-т времени t.

Для этого вводят понятие υ мгн.ск-ти.Она выч-ся так,берется очень короткий промежуток времени ∆t, за это время опр-т путь ∆S,тогда

v= ,чтобы опр-ть мгн.ск. мы должны сократить время до 0 и по этой же формуле выч-ть пример,получим

υ=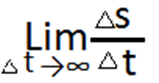

6. Вычисление производной функции по нашему определению. 1) значению х дадим превращение , получим . 2) получим значение f(x) и f( ) и их разность для функций ,

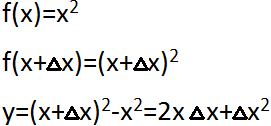. 3) составим отношение 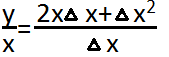и вычислим предел 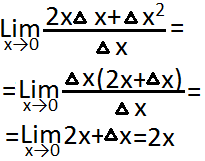итак производная y’=(x2)’=2x.

7.

8. Правило вычисления производных. Производная 2-го порядка .

Пр-р:у= sinx^3 y’=(sinx^3)’=cosx^3*3x^2=3x^2cosx^3

Производная от производной называется производной второго порядка. Обозначается y’’=(y’)’ или f’’(x).

Частные производные второго порядка.

Как и для функций одной переменной y=f(x) для которой можно вычислить производные второго и третьего порядка, можно вычислить производные второго порядка для функций z=f(x,y). Это значит от вычисленной производной надо вычислить еще раз производную. Вторые частные производные обозначаются последнее читается «дэ дважды от z по дэ икс в квадрате». Очевидно, что от частных производных по x Z’x можно вычислить частную производную по y, обозначается Z’’xy. Также можно вычислить от частной производной Z’y производную по x – Z’’yx.

Дифференциал функции двух переменных вычисляется аналогично одной переменной. y=f(x) dy=f(x)dx. Тогда для функции двух переменных z=f(x,y) также надо вычислить частные производные f’x и f’y, а затем домножить первое на dx, а второе на dy, затем взять их сумму. Получим dz=f’xdx+d’ydy

9. Механический смысл производной это мгновенная скорость v=s’(t). Пусть неравномерная скорость задается s=s(t), где s- путь, t-время. Средняя скорость определяется по формуле v= . Чтобы определить мгновенную скорость надо брать как можно короче время, т.е. дельта t стремится к 0. этот предел равенмгновенной скорости движения.

Геометрический смысл производной это угловой коэффициент касательной, т.е. f’(x)=k угловой коэффициент. Угловым коэффициентом k называется число равное k=tga(а-альфа), где а-угол от оси Ох до прямой.

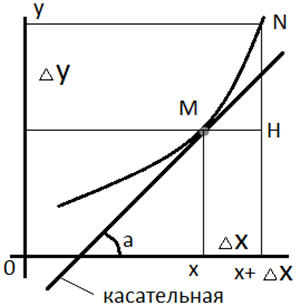
в треугольнике MNH NH=y MH=dx, то tga= . В треугольниках по касательной и по графику y=f(x) значение tga почти одинаковы и точно равны при дельта x стремящемся к 0. С одной стороны это производная, с другой стороны это угловой коэффициент касательной. Значит они равны.

10.Функция y=f(x) называется возрастающей если из x2>x1 следует f(x2) > f(x1)

Функция y=f(x) называется убывающей если х2>x1, следует f(x2)<f(x1)

Если функция y=f(x) дифференцируема на промежутке (а,в) и ее значение f(x)>0 на (а,в), и ее значение функция y=f(x) возрастает на (а,в).

Т.x0 для функции y=f(x) назыв,точкой максимума Xmax,если в левой окрестности функция возрастает а в правой окрестности убывает.

Т. х0 назыв точкой минимума если в окрестностях т.х0 значения f(x)>f(x0)

Для того чтобы точка х0 была точкой максимума необходимо и достаточно,чтобы производная f ‘(x0)=0 или не сущ,и производной f(x) в окрестности т.х0 меняла знак y’>0 на y<0(т.е с «+» на «-»)

11. Применение производной 2-го порядка для определения промежутков выпуклости и вогнутости графика , точки перегиба и вида экстремума.

Производная от производной называется производной второго порядка. Обозначается y’’=(y’)’ или f’’(x). Аналогично существует производные 3, 4, 5-го порядка. Производные высших порядков обозначаются римскими цифрами.

Выпуклость и вогнутость графика.

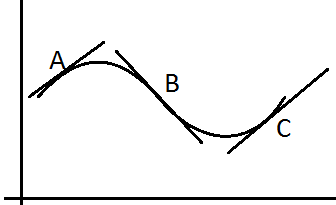на рисунке построен график дифференцируемой функции y=f(x). В точках А, В, и С построены касательные к графику. График дифференцируемой функции y=f(x) называется выпуклым (вогнутым) в интервале (a, b), если он является выпуклым (вогнутым) в каждой своей точке с первой координатой из (a, b). На рисунке график между точками А и В является выпуклым, а между точками В и С – вогнутым. Точка графика при переходе через которую график меняет выпуклость на вогнутость и наоборот, называется точкой перегиба. Если вторая производная f’’(x) функции y=f(x) положительна (отрицательна) в интервале (a, b), то график этой функции является вогнутым (выпуклым) в этом интервале. Если вторая производная f’’(x) функции y=f(x) обращается в точке x0 в нуль и при переходе через эту точку меняет знак, то точка (x0; f(x0)) графика данной функции является точкой перегибы.

12. Дифференциал функции. Формулы приближенных вычислений . Примеры.

Дифференциал функции одной переменной.

Пусть задана функция y=f(x) и известная производная y’=f’(x). По определению производной , где -приращение функции.

. Без предела можно записать или 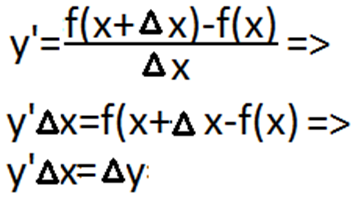Величина приращения функции через производную y’ и приращение называется дифференцированием, т.е. если взять предел , то имеем

13.Ф-ия F(x) наз-ся первообразной для f(x).(F(x))’=f(x).Н-р, для f=2x перв-й будет F(x)= х^2.т.к. (х^2)’=2x

Для ф-ий f(x) мн-во всех перв-х F(x)+C ф-ии наз-ся неопределенным интегралом, действие нахождения перв-й наз-ся интегрированием.Указ-е опр-е и действие запис-ся: Sf(x)dx=F(x)+C,C э R

Н-р:S2xdx=x^2+с

Св-ва неопр-го интеграла:

Т.к. операции интегрирования дифференцирования ,то верно интеграл

1) (Sf(x)dx)’=f(x).

2) (Sf(x)=f(x)dx

3) Sk+f(x)dx=kSf(x)dx

4)S(f(x))+-g(x)dx=Sf(x)dx+-Sg(x)dx

5)Sf(kx+b)dx=1/kF(kx+b)+C

14. Таблица интегралов

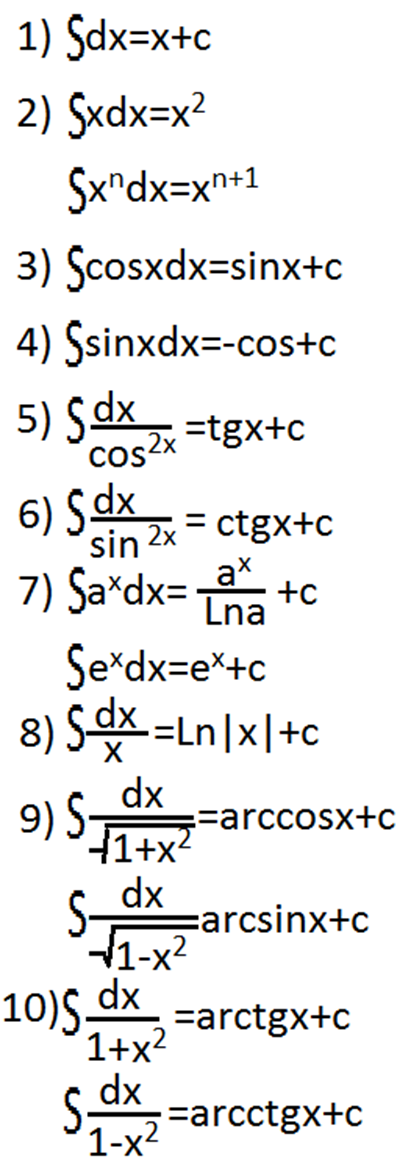
15. Непосредственное интегрирование , интегрирование подстановкой. Интегрирование по частям. Примеры.

Метод интегрирования подстановкой.

Вычисление интеграла подстановкой. В под интегральной функции f(x) заминают сложное выражение на простое. Например: . Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации. Формула интегрирования по частям следующая .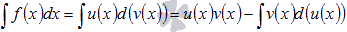

Интегрирование дробей. При интегрирование дробей данную дробь надо разложить на сумму простых дробей. При этом знаменатели дробей в произведение дают знаменатель данной дроби. Числитель дробей обозначают через А и B и находят их. Это метод неопределенных коэффициентов. Интегрирование тригонометрических функций по известным нам формулам тригонометрии под интегральные функции f(x) упрощает до интегралов из таблицы 3-6