Идеальный газ. Основное уравнение мкт.

    Известно, что частицы в газах, в отличие от жидкостей и твердых тел, располагаются друг относительно друга на расстояниях, существенно превышающих их собственные размеры. В этом случае взаимодействие между молекулами пренебрежимо мало и кинетическая энергия молекул много больше энергии межмолекулярного взаимодействия. Для выяснения наиболее общих свойств, присущих всем газам, используют упрощенную модель реальных газов - идеальный газ. Основные отличия идеального газа от реального газа:

1. Частицы идеального газа - сферические тела очень малых размеров, практически материальные точки. 2. Между частицами отсутствуют силы межмолекулярного взаимодействия. 3. Соударения частиц являются абсолютно упругими.

   Реальные разреженные газы действительно ведут себя подобно идеальному газу. Воспользуемся моделью идеального газа для объяснения происхождения давления газа. Вследствие теплового движения, частицы газа время от времени ударяются о стенки сосуда. При каждом ударе молекулы действуют на стенку сосуда с некоторой силой. Складываясь друг с другом, силы ударов отдельных частиц образуют некоторую силу давления, постоянно действующую на стенку. Понятно, что чем больше частиц содержится в сосуде, тем чаще они будут ударяться о стенку сосуда, и тем большей будет сила давления, а значит и давление. Чем быстрее движутся частицы, тем сильнее они ударяют в стенку сосуда. Мысленно представим себе простейший опыт: катящийся мяч ударяется о стенку. Если мяч катится медленно, то он при ударе подействует на стенку с меньшей силой, чем если бы он двигался быстро. Чем больше масса частицы, тем больше сила удара. Чем быстрее движутся частицы, тем чаще они ударяются о стенки сосуда. Итак, сила, с которой молекулы действуют на стенку сосуда, прямо пропорциональна числу молекул, содержащихся в единице объема (это число называется концентрацией молекул и обозначается n), массе молекулы m_o, среднему квадрату их скоростей и площади стенки сосуда. В результате получаем: давление газа прямо пропорционально концентрации частиц, массе частицы и квадрату скорости частицы (или их кинетической энергии). Зависимость давления идеального газа от концентрации и от средней кинетической энергии частиц выражается основным уравнением молекулярно-кинетической теории идеального газа. Мы получили основное уравнение МКТ идеального газа из общих соображений, но его можно строго вывести, опираясь на законы классической механики. Приведем одну из форм записи основного уравнения МКТ: P=(1/3)· n· m_o· V².

Вопрос№14 Температура. Абсолютная температура. Термодинамическая шкала температур

Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Температура всех частей системы, находящейся в равновесии, одинакова. Если система не находится в равновесии, то между её частями, имеющими различную температуру, происходит теплопередача (переход энергии от более нагретых частей системы к менее нагретым), приводящая к выравниванию температур в системе.

Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).

Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.

Абсолютный ноль определён как 0 K, что равно −273.15 °C.

Единица термодинамической температуры Кельвина (К), называемая кельвином, определяется тройной точкой воды, т.е. температурой, при которой вода находится в равновесии со льдом и паром. Эта температура принята равной 273,16 К, чем и определяется термодинамическая шкала температуры. Данная шкала, предложенная Кельвином, основана на втором начале термодинамики. Если имеются два тепловых резервуара с постоянной температурой и обратимая тепловая машина, передающая тепло от одного из них другому в соответствии с циклом Карно, то отношение термодинамических температур двух резервуаров дается равенством T₂ /T₁ = –Q₂Q₁, где Q₂ и Q₁ – количества теплоты, передаваемые каждому из резервуаров (знак «минус» говорит о том, что у одного из резервуаров теплота отбирается). Таким образом, если температура более теплого резервуара равна 273,16 К, а теплота, отбираемая у него, вдвое больше теплоты, передаваемой другому резервуару, то температура второго резервуара равна 136,58 К. Если же температура второго резервуара равна 0 К, то ему вообще не будет передана теплота, поскольку вся энергия газа была преобразована в механическую энергию на участке адиабатического расширения в цикле. Эта температура называется абсолютным нулем. Термодинамическая температура, используемая обычно в научных исследованиях, совпадает с температурой, входящей в уравнение состояния идеального газа PV = RT, где P – давление, V – объем и R – газовая постоянная. Уравнение показывает, что для идеального газа произведение объема на давление пропорционально температуре. Ни для одного из реальных газов этот закон точно не выполняется. Но если вносить поправки на вириальные силы, то расширение газов позволяет воспроизводить термодинамическую шкалу температуры. См. также ТОМСОН, УИЛЬЯМ.

Вопрос№15 Термодинамические параметры газа. Уравнение Менделеева – Клапейрона.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V₁, имеет давление р₁ и находится при тем­пературе T₁. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р₂, V₂, T₂ (рис. 63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма1–1'), 2) изохорного (изохора 1'–2)

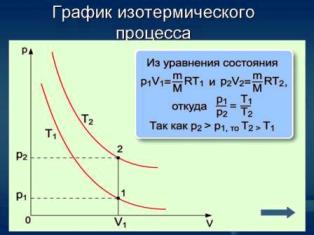
Вопрос№16 Изопроцессы и их графики.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма иадиабата соответственно. Изопроцессы являются частными случаями политропного процесса.