Инь Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. При рассмотрении вопросов, связанных с движением тел, можно не принимать   во внимание размеры тела. Тело, размерами которого в данных условиях можно пренебречь, называют материальной точкой. Положение тела (точки) в пространстве можно определить относительно какого-либо  другого тела, выбранного за тело отсчета A. Тело отсчета, связанная с ним система координат и часы составляют систему отсчета.  Характеристики механического движения тела: траектория (линия, вдоль которой движется тело) , перемещение (направленный отрезок  прямой, соединяющий начальное положение тела M1 с его последующим положением M2) , скорость (отношение перемещения ко времени  движения - для равномерного движения) . Характеристики механического движения относительны, т.е. они могут быть различными в  разных системах отсчета. Например, за движением лодки следят два наблюдателя: один на берегу в точке O, другой - на плоту в точке O1 (см.  рис.) . Проведем мысленно через точку О систему координат XOY - это неподвижная система отсчета. Другую систему X'O'Y' свяжем с  плотом - это подвижная система координат. Относительно системы X'O'Y' (плота) лодка за время t совершает перемещение и будет  двигаться со скоростью . Относительно системы XOY (берег) лодка за это же время совершит перемещение , , где -  перемещение плота относительно берега. Скорость лодки относительно берега или . Скорость тела относительно  неподвижной системы координат равна геометрической сумме скорости тела относительно подвижной системы и скорости этой системы  относительно неподвижной.     2. Виды механического движения - прямолинейное равномерное, прямолинейное равноускоренное, равномерное движение  по окружности

   В зависимости от формы траектории движение может быть прямолинейным и криволинейным. Движение называется  прямолинейным и равномерным, если за любые сколь угодно малые равные промежутки времени тело совершает одинаковые  перемещения. Запишем математическое выражение этого определения . Это значит, что перемещение определяют по  формуле , а координату - по формуле . Движение тела, при котором его скорость за любые равные промежутки времени изменяется  одинаково, называется равноускоренным движением. Для характеристики этого движения нужно знать скорость тела в данный момент  времени или в данной точке траектории, т.е. мгновенную скорость, а также ускорение. Мгновенная скорость - это отношение достаточно  малого перемещения на участке траектории, примыкающей к этой точке, к малому промежутку времени, в течение которого это перемещение  совершается. Ускорение - величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение  произошло. Иначе, ускорение - это быстрота изменения скорости: . Отсюда формула мгновенной скорости: . Перемещение  при этом движении определяют по формуле: . При равномерном движении по окружности углы поворота радиуса за любые равные  промежутки времени будут одинаковы. Поэтому угловая скорость , она измеряется в рад/с. При этом движении модуль скорости  постоянный, он направлен по касательной к траектории и постоянно меняет направление (см. рис.) , поэтому возникает  центростремительное ускорение . 

Вопрос№2. Равномерное, равноускоренное движение. Графики, формулы пути и скорости

Равномерным прямолинейным движением называют такое происходящее по прямолинейной траектории движение, при котором тело (материальная точка) за любые равные промежутки времени совершает одинаковые перемещения.

Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение:

v=s/t. 

Такое прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, называют равноускоренным прямолинейным движением.

Быстроту изменения скорости характеризуют величиной, обозначаемой а и называемой ускорением. Ускорением называют векторную величину, равную отношению изменения скорости тела v-v₀ к промежутку времени t, в течение которого это изменение произошло:

a=(v-v₀)/t. 

Вопрос№3 Свободное падение тел. Криволинейное движение.

Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте).

Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом   он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g оказывается неодинаковым, изменяясь примерно от 9,83 м/с² на полюсах до 9,78 м/с² на экваторе. На широте Москвы g = 9,81523 м/с². Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с² или даже 10 м/с².

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению. Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

Вопрос№4 Сила. Масса. Законы Ньютона.

Первый закон Ньютона: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерногопрямолинейного движения.

Второй закон Ньютона: В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

где   — ускорение материальной точки;  — равнодействующая всех сил, приложенных к материальной точке;  — масса материальной точки

Третий закон Ньютона: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Вопрос№5 Сила трения. Сила упругости. Закон Гука.

Закон Гука

Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена современником Ньютона английским физиком Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид

F=-kx,    (1)

где f - сила упругости; х - удлинение (деформация) тела; k - коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ - ньютон на метр (Н/м).

Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

Силы упругости

При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называетсякоэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.

В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

, где—   — коэффициент трения скольжения,

 си ла нормальной реакции опоры.

Вопрос№6 Закон Всемирного тяготения. Сила тяжести. Вес и невесомость.

Закон всемирного тяготения.

Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ныКеплера) и, в частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович.

 

Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

 

Закон справедлив для: 1. Однородных шаров.

2. Для материальных точек.

3. Для концентрических тел.

Гравитационное взаимодействие существенно при больших массах.

Примеры:      

 Притяжение электрона к протону в атоме водорода    210^-11 Н.

 

Тяготение между Землей и Луной 210²⁰ Н.

 

Тяготение между Солнцем и Землей  3,510²² Н.

 

Применение: 1. Закономерности движения планет и их спутников. Уточнены законы Кеплера.

2. Космонавтика. Расчет движения спутников.

Внимание!: 1. Закон не объясняет причин тяготения, а только устанавливает количественные закономерности.

 2. В случае взаимодействия трех и более тел задачу о движении тел нельзя решить в общемвиде. Требуется учитывать "возмущения", вызванные другими телами (открытие Нептуна Адамсом и Леверье в 1846 г. и Плутона в 1930).

3. В случае тел произвольной формы требуется суммировать взаимодействия между малыми частями каждого тела.

Анализ закона:

1. Сила направлена вдоль прямой, соединяющей тела.

2. G - постоянная всемирного тяготения (гравитационная постоянная). Числовое значение зависит от выбора системы единиц.

 

В Международной системе единиц (СИ)        G=6,67^.10^-11 .

G=6,67^.10^-11

Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш с помощью крутильных весов в 1798 г.

 

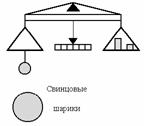
Пусть m₁=m₂=1 кг, R=1 м, тогда: G=F (численно).

Физический смысл гравитационной постоянной:

гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.

То, что гравитационная постоянная G очень мала показывает, что интенсивность гравитационного взаимодействия мала.

 

Сила тяжести

 

 

Сила тяжести - это сила притяжения тел к Земле (к планете).

 

 

 - из закона Всемирного тяготения. (где M - масса планеты, m - масса тела, R - расстояние до центра планеты).

 - сила тяжести из второго закона Ньютона (где m - масса тела, g - ускорение силы тяжести).

  - ускорение силы тяжести не зависит от массы тела (опыты Галилея).

G09,81 м/с2 - на поверхности Земли

Если обозначить R₀ радиус планеты, а h - расстояние до тела от поверхности планеты, то: 

Ускорение силы тяжести зависит:

1.      Массы планеты.

2.      Радиуса планеты.

3.      От высоты над поверхностью планеты.

4.      От географической широты (на полюсах - 9,83 м/с². на экваторе - 9,79 м/с².

5.      От залежей полезных ископаемых.

Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Пусть тело лежит на неподвижном относительно Земли горизонтальном столе (рис. 1.11.1). Систему отсчета, связанную с Землей, будем считать инерциальной. На тело действуют сила тяжести   направленная вертикально вниз, и сила упругости   с которой опора действует на тело. Силу   называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга:   В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой   равной по модулю силе реакции опоры и направленной в противоположную сторону:   По определению, сила   и называется весом тела. Из приведенных выше соотношений видно, что   т. е. вес тела   равен силе тяжести   Но эти силы приложены к разным телам!

Невесо́мость — состояние, при котором сила взаимодействия тела с опорой (вес тела), возникающая в связи с гравитационным притяжением, действием других массовых сил, в частности силы инерции, возникающей при ускоренном движении тела, отсутствует.

Вопрос№7 Импульс тела. Закон сохранения импульса.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

Импульс тела - это физическая векторная величина, равная произведению массы тела на его скорость.

 Если тело покоится, то его импульс равен нулю. Логично. Если скорость тела изменяется, то у тела появляется некий импульс, который характеризует величину приложенной к нему силы.

Закон сохранения импульса для двух тел в виде формулы будет выглядеть следующим образом:

(p_1' ) +(p_2' ) = (p_1 ) + (p_2 ),

Вопрос№8 Механическая работа. Мощность.

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы^[1]. Работой A, совершаемой постоянной силой   называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы   и перемещения   (рис. 1.18.1): 

A = Fs cos α.

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с. 

Вопрос№9 Механическая энергия и ее виды. Закон сохранения энергии

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципомсохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.