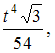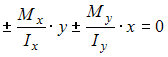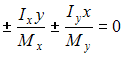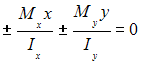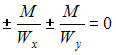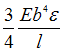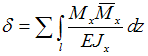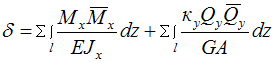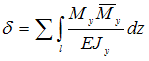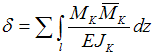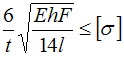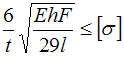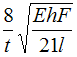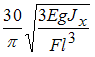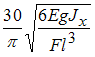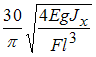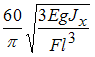- •Введение в курс
- •1.1. Основные понятия, определения, допущения и принципы
- •Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов: 3) упругостью
- •1.2. Модели прочностной надежности
- •1) Стержнем;
- •1.3. Внутренние силы и напряжения
- •1.4. Перемещения и деформация
- •Растяжение и сжатие
- •2.1. Продольная сила. Напряжения и деформации
- •2.2. Испытание конструкционных материалов на растяжение и сжатие
- •2.3. Механические свойства материалов
- •2.4. Расчеты стержней на прочность и жесткость
- •Сдвиг. Кручение
- •3.1. Чистый сдвиг. Расчет на сдвиг (срез)
- •3.2. Крутящий момент. Деформации и напряжения
- •3.3. Расчет на прочность при кручении
- •3.4. Расчет на жесткость при кручении
- •4. Напряженное состояние в точке. Главные площадки и главные напряжения
- •4.2. Виды напряженного состояния
- •4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
- •4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
- •5. Плоский прямой изгиб
- •5.1. Поперечная сила, изгибающий момент и их эпюры
- •5.2. Напряжения в поперечном сечении стержня при плоском изгибе
- •5.3. Расчет балок на прочность
- •5.4. Перемещения при изгибе. Расчет балок на жесткость
- •6.Сложное сопротивление
- •6.1. Виды нагружения стержня
- •6.2. Пространственный и косой изгиб
- •6.3. Изгиб с растяжением-сжатием
- •6.4. Изгиб с кручением
- •7.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина
- •7.2. Статическая неопределимость. Степень статической неопределенности
- •7.3.Метод сил
- •7.4. Расчет простейших статически неопределимых систем
- •8.1. Расчеты на прочность с учетом сил инерции
- •8.2. Прочность при ударных нагрузках
- •Увеличатся в 2 Ответ верный! ______________________________________________________________________
- •8.3. Расчеты на прочность при колебаниях
- •Упругая система с грузом массой m и жесткостью с имеет одну степень свободы. Круговая частота собственных колебаний системы равна …
- •8.4. Расчеты на прочность при напряжениях, периодически меняющихся во времени
- •График пульсационного цикла показан на схеме …
- •9. 1. Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
- •9.2. Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
- •9.3. Влияние условий закрепления концов стержня на величину критической силы
- •9.4. Устойчивость за пределом пропорциональности. Расчет сжатых стержней
- •10.1. Статические моменты. Центр тяжести плоской фигуры
- •10.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
- •5.3. Главные оси и главные моменты инерции
- •10.4. Моменты инерции простых и сложных сечений
5.3. Главные оси и главные моменты инерции
Задача 5.3.1:
Для сечения
известны осевые моменты инерции сечения
относительно осей
,
![]() ,
,
![]() :
:
![]() ,
,
![]() ,
,
![]() .
Осевой момент инерции относительно оси
.
Осевой момент инерции относительно оси
![]() равен…
равен…
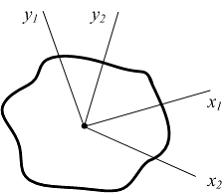 Вариант
ответа:
2500 см2
Вариант
ответа:
2500 см2
Задача 5.3.2: Из указанных центральных осей сечения равнобокого уголка главными являются…
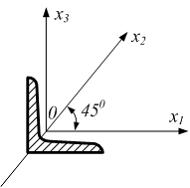 Вариант
ответа:
х2.
Вариант
ответа:
х2.
Задача 5.3.3: Главные оси инерции …
Вариант ответа: - можно провести через любую точку плоской фигуры.
Задача 5.3.4: Из указанных центральных осей главными осями сечения являются…
 Вариант ответа:
-
все
Вариант ответа:
-
все
Задача 5.3.5: Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются… Вариант ответа: - главными осями.
Задача 5.3.6:
Момент инерции
сечения относительно главной центральной
оси
![]() равен…
равен…
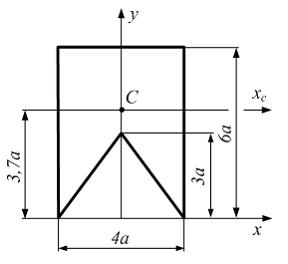 Вариант
ответа:
Вариант
ответа:
![]()
Тема:
Главные оси и главные моменты
инерции
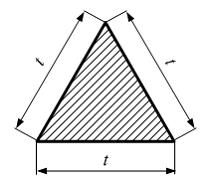 Число
главных центральных осей для равностороннего
треугольника …
Число
главных центральных осей для равностороннего
треугольника …
|
|
|
бесконечно велико |
Тема:
Главные оси и главные моменты
инерции
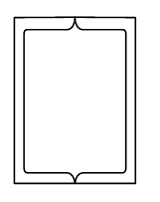 Главные
центральные моменты инерции фигуры,
состоящей из двух швеллеров №10, равны:
Главные
центральные моменты инерции фигуры,
состоящей из двух швеллеров №10, равны: ![]()
|
|
|
348; 258,5 |
Тема:
Главные оси и главные моменты
инерции
 Моменты
инерции треугольника относительно
осей x и y,
проходящих через центр тяжести поперечного
сечения, параллельно катетам:
Моменты
инерции треугольника относительно
осей x и y,
проходящих через центр тяжести поперечного
сечения, параллельно катетам:
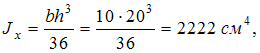

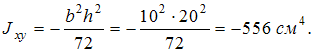 Положение
главных центральных осей определяется
углом
Положение
главных центральных осей определяется
углом ![]() а
главные центральные моменты инерции
равны
а
главные центральные моменты инерции
равны ![]()
|
|
|
|
Тема:
Главные оси и главные моменты инерции
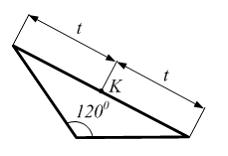 На
рисунке показан равнобедренный
треугольник. Моменты инерции относительно
главных осей, проходящих через точку К,
равны:
На
рисунке показан равнобедренный
треугольник. Моменты инерции относительно
главных осей, проходящих через точку К,
равны: ![]()
|
|
|
|
Тема: Главные оси и главные моменты инерции Главными центральными осями называются …
|
|
|
главные оси, проходящие через центр тяжести фигуры |
Тема: Главные оси и главные моменты инерциим
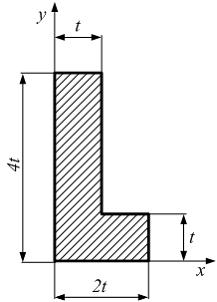 Моменты
инерции фигуры относительно осей x
и y:
Моменты
инерции фигуры относительно осей x
и y:
![]()
![]()
![]() Положение
главных осей, проходящих через начало
координат определяется углом равным …
Положение
главных осей, проходящих через начало
координат определяется углом равным …
|
|
|
|
Центробежный момент инерции может быть величиной …
|
|
|
положительной, отрицательнойя или равной нулю |
Тема: Главные оси и главные моменты инерциим
Плоская фигура имеет бесконечное множество главных центральных осей инерции, если число осей симметрии фигуры …
|
|
|
больше двух |
10.4. Моменты инерции простых и сложных сечений
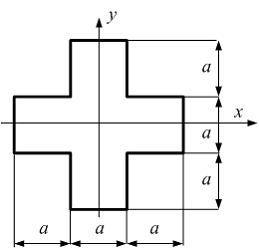
Задача 5.4.1:
Осевой момент инерции сечения относительно
оси
![]() равен…
равен…
 Вариант
ответа:
Вариант
ответа:
![]()
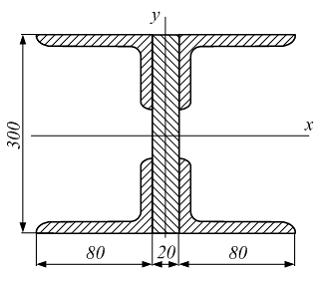
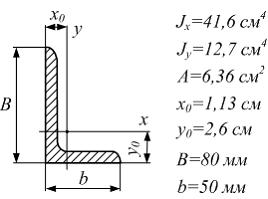
Задача 5.4.2:
Поперечное
сечение балки составлено из вертикального
листа и четырех неравнобоких уголков
![]() .
Характеристики уголка заданы. Размеры
на рисунке даны в мм. Моменты инерции
сечения
.
Характеристики уголка заданы. Размеры
на рисунке даны в мм. Моменты инерции
сечения
![]() и
и
![]() соответственно
равны…
соответственно
равны…
Вариант
ответа:
![]()
Задача 5.4.3: Момент инерции площади фигуры, состоящей из двух кругов, относительно оси x равен…
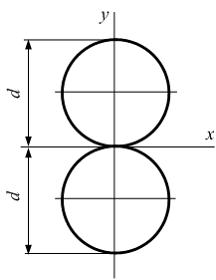 Вариант
ответа:
Вариант
ответа:
Задача 5.4.4: Момент инерции площади фигуры относительно оси x, проходящей через центр тяжести фигуры, равен …
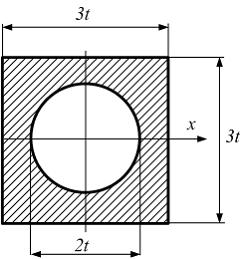 Вариант
ответа:
Вариант
ответа:
![]()
Задача 5.4.5: Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен…
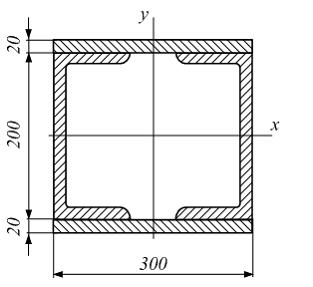
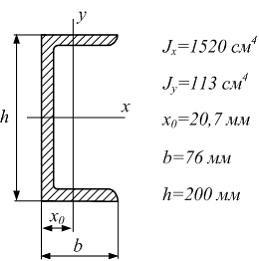
Вариант
ответа:
![]() .
.
Задача 5.4.6: Момент инерции сечения относительно оси равен…
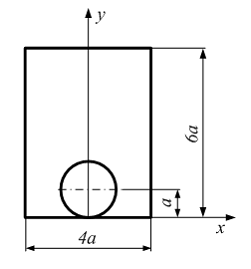 Вариант
ответа:
Вариант
ответа:
![]() .
.
Тема:
Моменты инерции простых и сложных
сечений
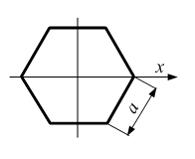 Момент
инерции правильного шестиугольника с
размером стороны а относительно
оси x равен …
Момент
инерции правильного шестиугольника с
размером стороны а относительно
оси x равен …
|
|
|
|
Тема:
Моменты инерции простых и сложных
сечений
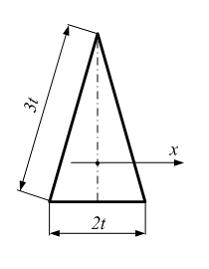 Момент
инерции равнобедренного треугольника
относительно оси x,
проходящей через центр тяжести параллельно
основанию, равен …
Момент
инерции равнобедренного треугольника
относительно оси x,
проходящей через центр тяжести параллельно
основанию, равен …
|
|
|
|
Тема:
Моменты инерции простых и сложных
сечений
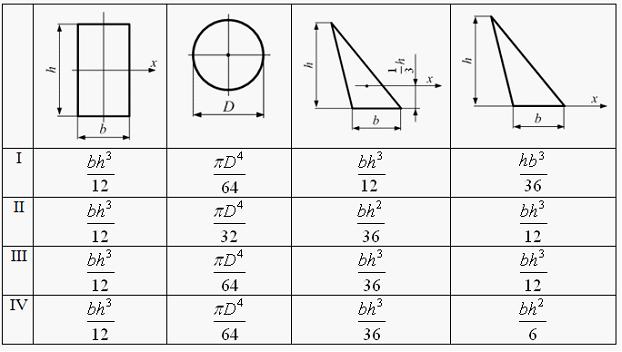 Моменты
инерции фигур относительно оси x определяются
по формулам варианта …
Моменты
инерции фигур относительно оси x определяются
по формулам варианта …
|
|
|
III |
Тема: Моменты инерции простых и сложных сечений
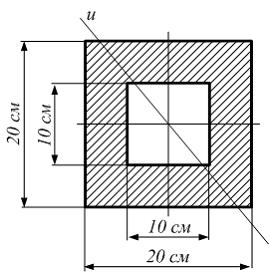 Осевой
момент инерции фигуры относительно оси
u
равен ____ см4.
Осевой
момент инерции фигуры относительно оси
u
равен ____ см4.
|
|
|
12500 |
Тема:
Моменты инерции простых и сложных
сечений
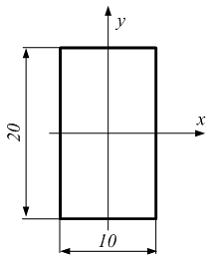 Размеры
фигуры даны в мм.
Момент инерции относительно оси x
равен ___ мм4.
Размеры
фигуры даны в мм.
Момент инерции относительно оси x
равен ___ мм4.
|
|
|
6666,7 |
Тема:
Моменты инерции простых и сложных
сечений
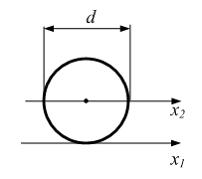 Ось
перемещается из положения x1 в
положение x2.
Момент инерции круга при этом …
Ось
перемещается из положения x1 в
положение x2.
Момент инерции круга при этом …
|
|
|
уменьшается
на величину |
Тема: Моменты инерции простых и сложных сечений
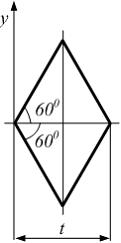 Осевой
момент инерции фигуры относительно оси
y равен ___
Осевой
момент инерции фигуры относительно оси
y равен ___
![]()
|
|
|
|
Тема: Моменты инерции простых и сложных сечений
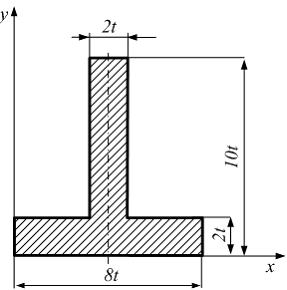 Центробежный
момент инерции фигуры относительно
осей x, y равен ____
Центробежный
момент инерции фигуры относительно
осей x, y равен ____
|
|
|
448 |
Тема: Моменты инерции простых и сложных сечений
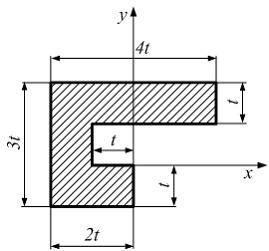 Центробежный
момент инерции фигуры относительной
осей x,
y
равен ____
Центробежный
момент инерции фигуры относительной
осей x,
y
равен ____
|
|
|
|
Кейс – задачи
Кейс-задания: Кейс 1 подзадача 1
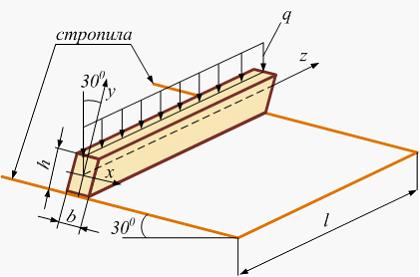 Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
Обрешетина
испытывает деформацию …
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
Обрешетина
испытывает деформацию …
|
|
|
косой изгиб |
Кейс-задания: Кейс 1 подзадача 2
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
![]() Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Прогиб среднего сечения в
направлении оси y
равен ____ см.
Влиянием поперечной силы пренебречь.
Прогиб вычислить с точностью до сотых.
Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Прогиб среднего сечения в
направлении оси y
равен ____ см.
Влиянием поперечной силы пренебречь.
Прогиб вычислить с точностью до сотых.
|
1,15
|
|
Кейс-задания: Кейс 1 подзадача 3
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
![]() Обрешетину
рассматриваем как балку, шарнирно
опертую по концам. Максимально допустимое
значение интенсивности q
из расчета на прочность равно ____
Обрешетину
рассматриваем как балку, шарнирно
опертую по концам. Максимально допустимое
значение интенсивности q
из расчета на прочность равно ____
![]() Конечный
результат округлить до целого числа.
Конечный
результат округлить до целого числа.
|
65 | |
Кейс-задания: Кейс 2 подзадача 1
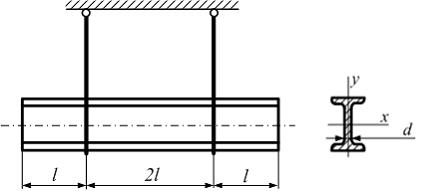 На
рисунке показана двутавровая балка №
50, подвешенная на двух троссах.
На
рисунке показана двутавровая балка №
50, подвешенная на двух троссах.
![]() –
погонный вес (вес части балки единичной
длины),
–
погонный вес (вес части балки единичной
длины),
![]() –
момент сопротивления поперечного
сечения,
–
момент сопротивления поперечного
сечения,
![]() –
статический момент полуплощади
поперечного сечения относительно оси
x,
–
статический момент полуплощади
поперечного сечения относительно оси
x,
![]() –
осевой момент инерции поперечного
сечения относительно оси x.
–
осевой момент инерции поперечного
сечения относительно оси x.
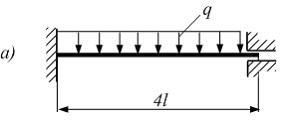
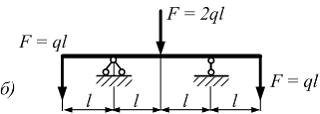
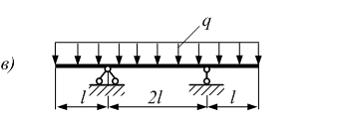
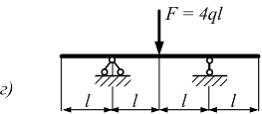 Расчетная
схема балки имеет вид …
Расчетная
схема балки имеет вид …
|
|
|
в |
Кейс-задания: Кейс 2 подзадача 2
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, касательное напряжение в поперечном сечении балки равно _____ кПа. (Ответ округлить до целого числа.)
|
559 | |
Кейс-задания: Кейс 2 подзадача 3
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычертить расчетную схему балки |
2 |
|
|
построить эпюру изгибающего момента от внешней нагрузки |
3 |
|
|
построить единичное состояние балки, приложив к среднему сечению единичную вертикальную силу |
4 |
|
|
построить эпюру изгибающего момента от единичной силы |
5 |
|
|
перемножить эпюры от внешней нагрузки и от единичной силы способом Верещагина |
Кейс-задания: Кейс 1 подзадача 1
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. При косом изгибе в поперечных сечениях стержня, в общем случае, действуют _________ внутренних силовых фактора(-ов).
|
|
|
четыре |
Кейс-задания: Кейс 1 подзадача 2
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
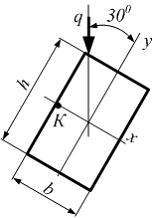
![]() Обрешетина
рассматривается как балка шарнирно
опертая по концам. Нормальное напряжение
в точке К
среднего поперечного сечения (см.
рисунок) равно _____ МПа.
Нормальное
напряжение вычислить с точностью до
сотых.
Обрешетина
рассматривается как балка шарнирно
опертая по концам. Нормальное напряжение
в точке К
среднего поперечного сечения (см.
рисунок) равно _____ МПа.
Нормальное
напряжение вычислить с точностью до
сотых.
|
20,25 | |
Кейс-задания: Кейс 1 подзадача 3
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
![]() Обрешетина
рассматривается как балка, шарнирно
опертая по концам. Максимально допустимая
длина пролета l
из расчета на прочность по допускаемым
напряжениям равна ___ м.
Длину
l
округлить до целого числа.
Обрешетина
рассматривается как балка, шарнирно
опертая по концам. Максимально допустимая
длина пролета l
из расчета на прочность по допускаемым
напряжениям равна ___ м.
Длину
l
округлить до целого числа.
|
4 | |
Кейс-задания: Кейс 2 подзадача 1
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Расчетная схема балки имеет вид …
|
|
|
в |
Кейс-задания: Кейс 2 подзадача 2
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, касательное напряжение в поперечном сечении балки равно _____ кПа. (Ответ округлить до целого числа.)
|
559 | |
Кейс-задания: Кейс 2 подзадача 3
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычертить расчетную схему балки |
2 |
|
|
построить эпюру изгибающего момента от внешней нагрузки |
3 |
|
|
построить единичное состояние балки, приложив к среднему сечению единичную вертикальную силу |
4 |
|
|
построить эпюру изгибающего момента от единичной силы |
5 |
|
|
перемножить эпюры от внешней нагрузки и от единичной силы способом Верещагина |
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Уравнение нейтральной линии при косом изгибе имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
![]() Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Угол поворота сечения над
опорой в плоскости yoz
равен …
Угол поворота вычислить с
точностью до десятых долей градуса.
Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Угол поворота сечения над
опорой в плоскости yoz
равен …
Угол поворота вычислить с
точностью до десятых долей градуса.
|
0,5 | |
Обрешетина
кровли из деревянного бруса подвергается
действию вертикальной равномерно
распределенной нагрузки с интенсивностью
q.
Нагрузка складывается из веса кровли
и снеговой нагрузки.
![]() Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Коэффициент запаса прочности
равен …
Значение коэффициента запаса
прочности округлить до целого числа.
Обрешетину
рассматриваем как балку шарнирно опертую
по концам. Коэффициент запаса прочности
равен …
Значение коэффициента запаса
прочности округлить до целого числа.
|
3 | |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Расчетная схема балки имеет вид …
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
г |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, касательное напряжение в поперечном сечении балки равно _____ кПа. (Ответ округлить до целого числа.)
|
559 | |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычертить расчетную схему балки |
2 |
|
|
построить эпюру изгибающего момента от внешней нагрузки |
3 |
|
|
построить единичное состояние балки, приложив к среднему сечению единичную вертикальную силу |
4 |
|
|
построить эпюру изгибающего момента от единичной силы |
5 |
|
|
перемножить эпюры от внешней нагрузки и от единичной силы способом Верещагина |
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Обрешетина испытывает деформацию …
|
|
|
косой изгиб |
|
|
|
плоский изгиб |
|
|
|
плоский изгиб с растяжением |
|
|
|
косой изгиб с кручением |
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Обрешетину рассматриваем как балку шарнирно опертую по концам. Прогиб среднего сечения в направлении оси y равен ____ см. Влиянием поперечной силы пренебречь. Прогиб вычислить с точностью до сотых.
|
1,15 |
|
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Обрешетину рассматриваем как балку, шарнирно опертую по концам. Максимально допустимое значение интенсивности q из расчета на прочность равно ____ Конечный результат округлить до целого числа.
|
65 |
|
На
рисунке показана двутавровая балка №
50, подвешенная на двух троссах.
–
погонный вес (вес части балки единичной
длины),
–
момент сопротивления поперечного
сечения,
–
статический момент полуплощади
поперечного сечения относительно оси
x,
–
осевой момент инерции поперечного
сечения относительно оси x.
Продольные
силы в тросах, определенные в общем
виде, равны:
![]()
|
|
|
2, 2 |
|
|
|
1, 2 |
|
|
|
1, 3 |
|
|
|
3, 3 |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, нормальное напряжение в поперечном сечении балки равно ____ кПа. (Ответ округлить до целого числа.)
|
2201 |
|
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычерчиваем расчетную схему балки |
2 |
|
|
строим эпюру изгибающих моментов |
3 |
|
|
определяем величину максимального нормального напряжения |
4 |
|
|
сравниваем величину максимального нормального напряжения с допускаемым |
Материал, у которого при переходе от одной точки к другой свойства, в зависимости от направления, изменяются по одному и тому же закону, является …
|
|
|
анизотропным, однородным |
|
|
|
изотропным, однородным |
|
|
|
анизотропным, неоднородным |
|
|
|
изотропным, неоднородным |
 Правый
конец балки (см. рисунок) необходимо
закрепить так, чтобы сечение С
не перемещалось вдоль координатных
осей z и y,
но могло бы поворачиваться в плоскости
zy.
Опора, отвечающая таким требованиям,
называется …
Правый
конец балки (см. рисунок) необходимо
закрепить так, чтобы сечение С
не перемещалось вдоль координатных
осей z и y,
но могло бы поворачиваться в плоскости
zy.
Опора, отвечающая таким требованиям,
называется …
|
|
|
шарнирно неподвижной |
|
|
|
шарнирно подвижной |
|
|
|
жестким защемлением |
|
|
|
скользящим защемлением |
Крутящий момент ( ) и изгибающие моменты и лежат в плоскостях …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
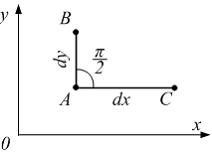 В
процессе деформации точки А,
В,
С
деформируемого тела перемещаются в
плоскости xoy,
а прямолинейные отрезки АВ
и АС
поворачиваются по часовой стрелке на
угол
В
процессе деформации точки А,
В,
С
деформируемого тела перемещаются в
плоскости xoy,
а прямолинейные отрезки АВ
и АС
поворачиваются по часовой стрелке на
угол
![]() Угловая
деформация в точке А
между направлениями АВ
и АС,
когда длины отрезков стремятся к нулю,
равна …
Угловая
деформация в точке А
между направлениями АВ
и АС,
когда длины отрезков стремятся к нулю,
равна …
|
|
|
нулю |
|
|
|
|
|
|
|
|
|
|
|
|
Стержень длиной l (см. рисунок) находится под действием собственного веса. Вес стержня Q, площадь поперечного сечения А, модуль упругости материала стержня Е – известны. Продольная линейная деформация в среднем сечении стержня равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характер разрушения образца из хрупкого материала при растяжении показан на рисунке …
|
|
|
а |
|
|
|
b |
|
|
|
c |
|
|
|
d |
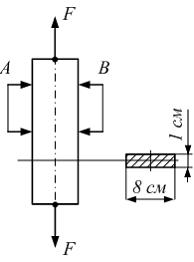 При
нагружении образца прямоугольного
сечения силами
При
нагружении образца прямоугольного
сечения силами
![]() стрелки
тензометров А и В переместились на 6 и
4 деления соответственно. Базы тензометров
– 20 мм.
Цена деления шкалы тензометров – 0,001
мм.
Модуль упругости материала образца
равен ____ МПа.
стрелки
тензометров А и В переместились на 6 и
4 деления соответственно. Базы тензометров
– 20 мм.
Цена деления шкалы тензометров – 0,001
мм.
Модуль упругости материала образца
равен ____ МПа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
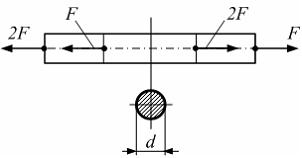 Стержень
растянут осевыми силами (см. рисунок).
Задана допустимая величина нормального
напряжения
для
материала стержня. Условие прочности
имеет вид …
Стержень
растянут осевыми силами (см. рисунок).
Задана допустимая величина нормального
напряжения
для
материала стержня. Условие прочности
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
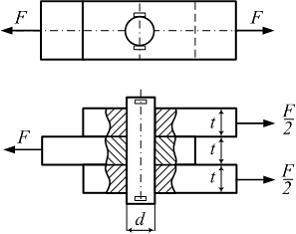 Три
металлические полосы (см. рисунок)
соединены штифтом.
Три
металлические полосы (см. рисунок)
соединены штифтом.
![]() –
значение допускаемого касательного
напряжения на срез для материала штифта.
Условие прочности штифта на срез имеет
вид …
–
значение допускаемого касательного
напряжения на срез для материала штифта.
Условие прочности штифта на срез имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При кручении стержня круглого поперечного сечения напряженное состояние материала во всех точках, за исключением точек на оси стержня, – …
|
|
|
чистый сдвиг |
|
|
|
линейное (одноосное растяжение) |
|
|
|
линейное (одноосное сжатие) |
|
|
|
объемное |
Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается …
|
|
|
предел текучести при чистом сдвиге |
|
|
|
предел текучести при растяжении |
|
|
|
предел прочности при чистом сдвиге |
|
|
|
предел упругости при чистом сдвиге |
На рисунке показан стержень, работающий на кручение. Известны величины: l, М. Угол поворота сечения С равен нулю, когда момент имеет значение …
|
|
|
|
|
|
|
М |
|
|
|
|
|
|
|
|
Нормальные напряжения, действующие на главных площадках, называются …
|
|
|
главными напряжениями |
|
|
|
экстремальными напряжениями |
|
|
|
октаэдрическими напряжениями |
|
|
|
инвариантами напряженного состояния |
Напряженные состояния в точках нагруженного тела бывают ______ видов.
|
|
|
трех |
|
|
|
двух |
|
|
|
четырех |
|
|
|
пяти |
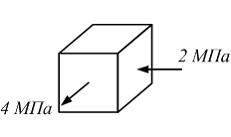 На
рисунке показано напряженное состояние
в точке. Материал хрупкий с пределом
прочности на растяжение
На
рисунке показано напряженное состояние
в точке. Материал хрупкий с пределом
прочности на растяжение
![]() и
пределом прочности на сжатие
и
пределом прочности на сжатие
![]() Коэффициент
Пуассона
Коэффициент
Пуассона
![]() Величина
эквивалентного напряжения равна _____
МПа,
прочность материала ______. Использовать
теорию наибольших линейных деформаций
удлинения.
Величина
эквивалентного напряжения равна _____
МПа,
прочность материала ______. Использовать
теорию наибольших линейных деформаций
удлинения.
|
|
|
4,34, не обеспечена |
|
|
|
4,34, обеспечена |
|
|
|
6, не обеспечена |
|
|
|
3,66, обеспечена |
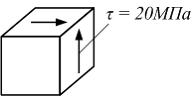 На
рисунке показано напряженное состояние
в точке. Модуль упругости
На
рисунке показано напряженное состояние
в точке. Модуль упругости
![]() ,
коэффициент Пуассона
,
коэффициент Пуассона
![]() Главные
линейные деформации
Главные
линейные деформации
![]() соответственно
равны …
соответственно
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рисунке показана система, состоящая из трех фигур. Точки и – центры тяжести второй и третьей фигур. Для того чтобы статический момент всей системы относительно оси у обратился в ноль, статический момент первой фигуры должен быть равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
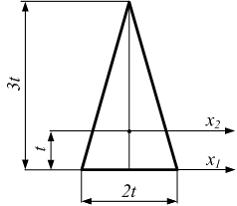 При
переходе от оси
к
оси
При
переходе от оси
к
оси
![]() осевой
момент инерции треугольника …
осевой
момент инерции треугольника …
|
|
|
уменьшится на
величину
|
|
|
|
увеличится на величину |
|
|
|
не изменится |
|
|
|
увеличится на
величину
|
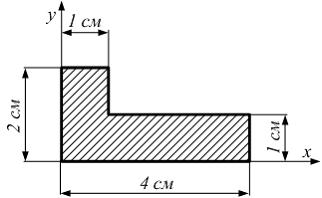 Моменты
инерции фигуры относительно осей x
и y:
Моменты
инерции фигуры относительно осей x
и y:
![]()
![]()
![]() Положение
главных осей, проходящих через начало
координат, определяется углом равным
…
Положение
главных осей, проходящих через начало
координат, определяется углом равным
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Осевой
момент инерции фигуры относительно оси
y
равен ____
Осевой
момент инерции фигуры относительно оси
y
равен ____
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однопролетная балка ВС длиной нагружена силой и равномерно распределенной нагрузкой интенсивности q. Максимальные значения изгибающего момента и поперечной силы по абсолютной величине соответственно равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Консольная балка прямоугольного сечения с размерами b и h нагружена силами F. Линейный размер . Отношение максимального нормального напряжения к максимальному касательному напряжению в балке равно …
|
|
|
60 |
|
|
|
40 |
|
|
|
80 |
|
|
|
10 |
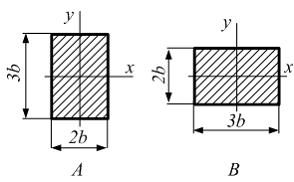 Балка
имеет прямоугольное поперечное сечение
с размерами
и
При
повороте поперечного сечения из положения
А
в положение В
грузоподъемность балки, из расчета по
нормальным напряжениям, …
Балка
имеет прямоугольное поперечное сечение
с размерами
и
При
повороте поперечного сечения из положения
А
в положение В
грузоподъемность балки, из расчета по
нормальным напряжениям, …
|
|
|
уменьшится в 1,5 раза |
|
|
|
не изменится |
|
|
|
уменьшится в 2 раза |
|
|
|
увеличится в 1,5 раза |
Консоль на половине длины нагружена равномерно распределенной нагрузкой интенсивности Модуль упругости материала балки размер Прогиб на свободном конце консоли не должен превышать Из условия жесткости диаметр поперечного сечения d равен ____ (см).
|
|
|
37,1 |
|
|
|
18,5 |
|
|
|
42,4 |
|
|
|
28,4 |
Схема нагружения стержня квадратного сечения внешними силами показана на рисунке (одна сила лежит в плоскости чертежа, вторая – перпендикулярно плоскости). Деформации (растяжение, кручение и плоский поперечный изгиб) одновременно возникают на участке (-ах) …
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
|
|
|
2, 3 |
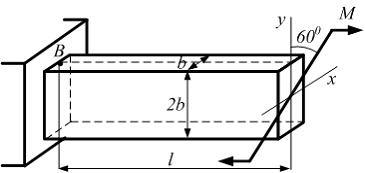 Стержень
длиной l
прямоугольного сечения с размерами b
и 2b
нагружен моментом М.
Плоскость действия момента расположена
под углом
Стержень
длиной l
прямоугольного сечения с размерами b
и 2b
нагружен моментом М.
Плоскость действия момента расположена
под углом
![]() к
оси y.
Модуль упругости материала Е,
размер b
известны. Линейная деформация в точке
В,
в направлении оси стержня, достигнет
значения
к
оси y.
Модуль упругости материала Е,
размер b
известны. Линейная деформация в точке
В,
в направлении оси стержня, достигнет
значения
![]() ,
если момент М
будет равен …
,
если момент М
будет равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Стержень
круглого сечения диаметром d
нагружен внешними силами. Значение
максимального нормального напряжения
в поперечном сечении стержня равно …
Стержень
круглого сечения диаметром d
нагружен внешними силами. Значение
максимального нормального напряжения
в поперечном сечении стержня равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стержень диаметром d, длиной l нагружен силами через абсолютно жесткий элемент длиной 2l. При удалении одной из сил грузоподъемность стержня ___. При решении задачи воспользоваться теорией наибольших касательных напряжений (III теория прочности).
|
|
|
увеличивается в раз |
|
|
|
увеличивается в 2 раза |
|
|
|
уменьшится в раз |
|
|
|
увеличится в раза |
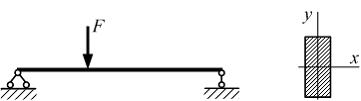 Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
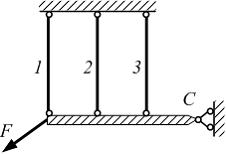 Степень
статической неопределимости системы
(см. рисунок) равна …
Степень
статической неопределимости системы
(см. рисунок) равна …
|
|
|
двум |
|
|
|
единице |
|
|
|
трем |
|
|
|
четырем |
Симметричными внутренними силовыми факторами являются …
|
|
|
изгибающие моменты и продольная сила |
|
|
|
крутящий момент и продольная сила |
|
|
|
продольная и поперечные силы |
|
|
|
поперечные силы и крутящий момент |
В середине пролета к балке прямоугольного сечения высотой h прикреплен стержень ВС с жесткостью поперечного сечения на растяжение ЕА. Жесткость поперечного сечения балки на изгиб EJ по длине постоянна (J – осевой момент инерции сечения). Линейный размер l задан. Максимальное нормальное напряжение в балке равно … Принять
|
|
|
|
|
|
|
|
|
|
|
|
Для сжатых стержней, помимо проверки на прочность, необходимо выполнить и проверку на …
|
|
|
устойчивость |
|
|
|
жесткость |
|
|
|
ползучесть |
|
|
|
выносливость |
Для стержня с шарнирно-опертыми концами значению критической силы соответствует изгиб стержня по …
|
|
|
полуволне синусоиды |
|
|
|
квадратичной параболе |
|
|
|
дуге окружности |
|
|
|
синусоиде |
Стержень, схема закрепления которого показана на верхнем рисунке, сжимается силой F. Форма потери устойчивости стержня представлена на схеме …
|
|
|
в |
|
|
|
а |
|
|
|
г |
|
|
|
б |
Допускаемое напряжение на устойчивость и допускаемое напряжение на прочность связаны отношением . Коэффициент называют …
|
|
|
коэффициентом уменьшения основного допускаемого напряжения |
|
|
|
теоретическим коэффициентом концентрации напряжений |
|
|
|
коэффициентом чувствительности материала к асимметрии цикла |
|
|
|
коэффициентом динамичности системы |
Если к системе, движущейся ускоренно, кроме активных и реактивных сил приложить силы инерции, то получим уравновешенную систему сил, которая удовлетворяет уравнениям равновесия статики. Данное положение называется принципом …
|
|
|
Д΄Аламбера |
|
|
|
Сен-Венана |
|
|
|
суперпозиции |
|
|
|
начальных размеров |
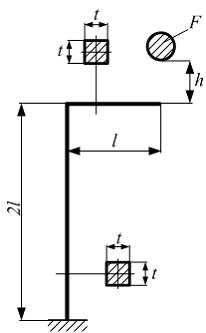 На
раму с высоты h
падает груз весом F.
Размеры l
и t,
допускаемое нормальное напряжение
На
раму с высоты h
падает груз весом F.
Размеры l
и t,
допускаемое нормальное напряжение
![]() ,
модуль упругости Е
заданы.
Условие прочности для рамы имеет вид
…
При определении динамического
коэффициента использовать приближенную
формулу
,
модуль упругости Е
заданы.
Условие прочности для рамы имеет вид
…
При определении динамического
коэффициента использовать приближенную
формулу
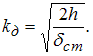 Продольную
силу в расчетах не учитывать.
Продольную
силу в расчетах не учитывать.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
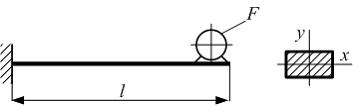 На
балку установлен электродвигатель, в
котором имеется несбалансированная
вращающаяся масса. Размер l,
осевой момент инерции поперечного
сечения
,
модуль упругости Е,
вес электродвигателя F
заданы. Выражение для числа оборотов в
минуту электродвигателя, при котором
наступает резонанс, имеет вид … Балку
с двигателем рассматривать как систему
с одной степенью свободы. Массу балки
в расчетах не учитывать.
На
балку установлен электродвигатель, в
котором имеется несбалансированная
вращающаяся масса. Размер l,
осевой момент инерции поперечного
сечения
,
модуль упругости Е,
вес электродвигателя F
заданы. Выражение для числа оборотов в
минуту электродвигателя, при котором
наступает резонанс, имеет вид … Балку
с двигателем рассматривать как систему
с одной степенью свободы. Массу балки
в расчетах не учитывать.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диаграмма предельных амплитуд напряжений при асимметричных циклах строится в координатах …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
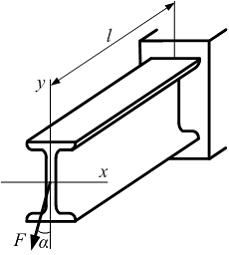 На
рисунке показана двутавровая балка
На
рисунке показана двутавровая балка
![]() один
конец которой жестко защемлен, а другой
свободен. Балка нагружена силой F,
лежащей в плоскости поперечного
сечения.
один
конец которой жестко защемлен, а другой
свободен. Балка нагружена силой F,
лежащей в плоскости поперечного
сечения.
![]()
![]()
![]()
![]()
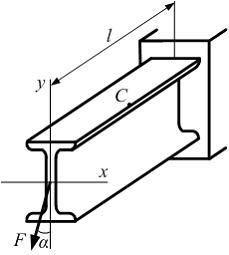 Напряженное
состояние в точке С
поперечного сечения балки – …
Напряженное
состояние в точке С
поперечного сечения балки – …
|
|
|
линейное |
|
|
|
объемное |
|
|
|
плоское |
|
|
|
плоское (чистый сдвиг) |
На рисунке показана двутавровая балка один конец которой жестко защемлен, а другой свободен. Балка нагружена силой F, лежащей в плоскости поперечного сечения. Горизонтальное перемещение свободного конца балки равно ____ мм. (Ответ округлить до целого числа.)
|
6 |
|
На рисунке показана двутавровая балка один конец которой жестко защемлен, а другой свободен. Балка нагружена силой F, лежащей в плоскости поперечного сечения. Максимальное нормальное напряжение в поперечном сечении балки, по абсолютной величине, равно ____ МПа. (Ответ округлить до целого числа.)
|
195 |
|
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Расчетная схема балки имеет вид …
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
г |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычертить расчетную схему балки |
2 |
|
|
построить эпюру изгибающего момента от внешней нагрузки |
3 |
|
|
построить единичное состояние балки, приложив к среднему сечению единичную вертикальную силу |
4 |
|
|
построить эпюру изгибающего момента от единичной силы |
5 |
|
|
перемножить эпюры от внешней нагрузки и от единичной силы способом Верещагина |
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, касательное напряжение в поперечном сечении балки равно _____ кПа. (Ответ округлить до целого числа.)
|
559 |
|
Кейс-задания: Кейс 1 подзадача 1
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Уравнение нейтральной линии при косом изгибе имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кейс-задания: Кейс 1 подзадача 2
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Обрешетину рассматриваем как балку шарнирно опертую по концам. Угол поворота сечения над опорой в плоскости yoz равен … Угол поворота вычислить с точностью до десятых долей градуса.
|
0,5 | |
Кейс-задания: Кейс 1 подзадача 3
Обрешетина кровли из деревянного бруса подвергается действию вертикальной равномерно распределенной нагрузки с интенсивностью q. Нагрузка складывается из веса кровли и снеговой нагрузки. Обрешетину рассматриваем как балку шарнирно опертую по концам. Коэффициент запаса прочности равен … Значение коэффициента запаса прочности округлить до целого числа.
|
3 | |
Кейс-задания: Кейс 2 подзадача 1
На рисунке показано схематическое изображение мостового крана пролетом l, состоящего из двутавра и тележки. Кран поднимает или опускает груз весом F с ускорением а. Принцип, сводящий задачу об ускоренном движении тела к статической задаче, называется принципом …
|
|
|
Даламбера |
|
|
|
Сен–Венана |
|
|
|
суперпозиции |
|
|
|
начальных размеров |
Кейс-задания: Кейс 2 подзадача 2
На рисунке показано
схематическое изображение мостового
крана пролетом l,
состоящего из двутавра и тележки. Кран
поднимает или опускает груз весом F
с ускорением а.
Груз
весом F
= 10 кН,
подвешенный на тросе, поднимается с
ускорением
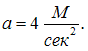 Диаметр
троса d
= 1см.
Нормальное напряжение в поперечном
сечении троса равно ____ МПа.
Ускорение свободного падения принять
равным
Диаметр
троса d
= 1см.
Нормальное напряжение в поперечном
сечении троса равно ____ МПа.
Ускорение свободного падения принять
равным
![]() Расчеты
производить с точностью до сотых.
Окончательный результат округлить до
целого числа.
Расчеты
производить с точностью до сотых.
Окончательный результат округлить до
целого числа.
|
177 | |
мКейс-задания: Кейс 2 подзадача 3
На рисунке показано схематическое изображение мостового крана пролетом l, состоящего из двутавра и тележки. Кран поднимает или опускает груз весом F с ускорением а. Укажите правильную последовательность указанных действий.
1 |
|
|
Определяем реакции опор двутавровой балки |
2 |
|
|
Строим эпюру изгибающего момента |
3 |
|
|
По эпюре изгибающего момента определяем максимальный, по абсолютной величине, момент |
4 |
|
|
Определяем момент сопротивления поперечного сечения двутавра заданного номера (по ГОСТу) и величину максимального нормального напряжения |
Кейс-задания: Кейс 1 подзадача 1
 Колонна
здания прямоугольного поперечного
сечения нагружена силой F
в точке K.
Колонна
здания прямоугольного поперечного
сечения нагружена силой F
в точке K.
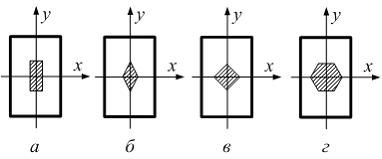 Ядро
поперечного сечения колонны имеет вид,
показанный на рисунке …
Ядро
поперечного сечения колонны имеет вид,
показанный на рисунке …
|
|
|
б |
|
|
|
в |
|
|
|
г |
|
|
|
а |
мммКейс-задания: Кейс 1 подзадача 2
Колонна
здания прямоугольного поперечного
сечения нагружена силой F
в точке K.
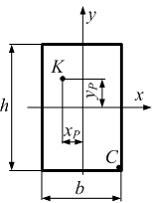
![]() Нормальное
напряжение в точке С
поперечного сечения равно ____ МПа.
Значение нормального напряжения в точке
С
округлить до целого числа.
Нормальное
напряжение в точке С
поперечного сечения равно ____ МПа.
Значение нормального напряжения в точке
С
округлить до целого числа.
|
6 | |
Кейс-задания: Кейс 1 подзадача 3
Колонна
здания прямоугольного поперечного
сечения нагружена силой F
в точке K.
b
= 10 см,
h
= 20 см.
Напряжение в центре тяжести поперечного
сечения при центральном сжатии силой
F
![]() известно
и равно 9 МПа.
Если силу F
переместить в точку с координатами
известно
и равно 9 МПа.
Если силу F
переместить в точку с координатами
![]() то
напряжение в центре тяжести поперечного
сечения будет равно _____ МПа.
то
напряжение в центре тяжести поперечного
сечения будет равно _____ МПа.
|
9 | |
Кейс-задания: Кейс 2 подзадача 1
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Продольные силы в тросах, определенные в общем виде, равны:
|
|
|
2, 2 |
|
|
|
1, 2 |
|
|
|
1, 3 |
|
|
|
3, 3 |
Кейс-задания: Кейс 2 подзадача 2
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Максимальное, по абсолютной величине, нормальное напряжение в поперечном сечении балки равно ____ кПа. (Ответ округлить до целого числа.)
|
2201 | |
Кейс-задания: Кейс 2 подзадача 3
На рисунке показана двутавровая балка № 50, подвешенная на двух троссах. – погонный вес (вес части балки единичной длины), – момент сопротивления поперечного сечения, – статический момент полуплощади поперечного сечения относительно оси x, – осевой момент инерции поперечного сечения относительно оси x. Укажите правильную последовательность указанных действий.
1 |
|
|
вычерчиваем расчетную схему балки |
2 |
|
|
строим эпюру изгибающих моментов |
3 |
|
|
определяем величину максимального нормального напряжения |
4 |
|
|
сравниваем величину максимального нормального напряжения с допускаемым напряжением |