
- •Введение в курс
- •1.1. Основные понятия, определения, допущения и принципы
- •Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов: 3) упругостью
- •1.2. Модели прочностной надежности
- •1) Стержнем;
- •1.3. Внутренние силы и напряжения
- •1.4. Перемещения и деформация
- •Растяжение и сжатие
- •2.1. Продольная сила. Напряжения и деформации
- •2.2. Испытание конструкционных материалов на растяжение и сжатие
- •2.3. Механические свойства материалов
- •2.4. Расчеты стержней на прочность и жесткость
- •Сдвиг. Кручение
- •3.1. Чистый сдвиг. Расчет на сдвиг (срез)
- •3.2. Крутящий момент. Деформации и напряжения
- •3.3. Расчет на прочность при кручении
- •3.4. Расчет на жесткость при кручении
- •4. Напряженное состояние в точке. Главные площадки и главные напряжения
- •4.2. Виды напряженного состояния
- •4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
- •4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
- •5. Плоский прямой изгиб
- •5.1. Поперечная сила, изгибающий момент и их эпюры
- •5.2. Напряжения в поперечном сечении стержня при плоском изгибе
- •5.3. Расчет балок на прочность
- •5.4. Перемещения при изгибе. Расчет балок на жесткость
- •6.Сложное сопротивление
- •6.1. Виды нагружения стержня
- •6.2. Пространственный и косой изгиб
- •6.3. Изгиб с растяжением-сжатием
- •6.4. Изгиб с кручением
- •7.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина
- •7.2. Статическая неопределимость. Степень статической неопределенности
- •7.3.Метод сил
- •7.4. Расчет простейших статически неопределимых систем
- •8.1. Расчеты на прочность с учетом сил инерции
- •8.2. Прочность при ударных нагрузках
- •Увеличатся в 2 Ответ верный! ______________________________________________________________________
- •8.3. Расчеты на прочность при колебаниях
- •Упругая система с грузом массой m и жесткостью с имеет одну степень свободы. Круговая частота собственных колебаний системы равна …
- •8.4. Расчеты на прочность при напряжениях, периодически меняющихся во времени
- •График пульсационного цикла показан на схеме …
- •9. 1. Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
- •9.2. Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
- •9.3. Влияние условий закрепления концов стержня на величину критической силы
- •9.4. Устойчивость за пределом пропорциональности. Расчет сжатых стержней
- •10.1. Статические моменты. Центр тяжести плоской фигуры
- •10.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
- •5.3. Главные оси и главные моменты инерции
- •10.4. Моменты инерции простых и сложных сечений
1.4. Перемещения и деформация
Задача 1.4.1: Упрощение, на основании которого при составлении уравнений равновесия тело, после нагружения внешними силами рассматривают как недеформированное, называется…
Варианты ответов: 2) принципом начальных размеров;
Задача 1.4.2:
Первоначальная
длина стержня равна l.
После приложения растягивающей силы
длина стержня стала l1.
Величина
![]() называется…
называется…
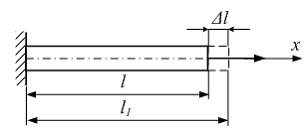
Варианты ответов: 1) абсолютным удлинением;
Задача 1.4.3: Угловым перемещением сечения (см. рис.) является величина…
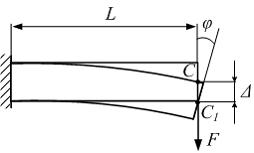
Варианты
ответов: 2)
![]() ;
;
Задача 1.4.4: Количественная мера изменения геометрических размеров в окрестности точки называется…
Варианты ответов: 3) линейной деформацией
Задача 1.4.5: В
результате действия внешних сил на
деформируемое тело точка К заняла новое
положение К1.
Вектор
![]() называется…
полным перемещением;
называется…
полным перемещением;
Тема: Перемещения и деформации Размерность линейной деформации – … |
|
|
|
|
||||||||||||
Тема:
Перемещения и деформации
Если
известны углы поворота малого
прямолинейного отрезка в трех
координатных плоскостях |
|
|
|
|||||||||||||
Тема: Перемещения и деформации Угловая деформация − это … |
|
|
изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку. |
|||||||||||||
Тема:
Перемещения и деформации
|
|
|
|
|||||||||||||
Тема: Перемещения и деформации Вектор полного линейного перемещения точки в общем случае … |
|
|
можно разложить на три составляющих вектора, направленных вдоль координатных осей |
|||||||||||||
Тема: Перемещение и деформация
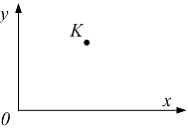 Точка
К
деформируемого тела перемещается в
плоскости xoy.
Полное перемещение равно 5 мм.
В направлении оси y
точка переместилась на величину 3 мм.
Перемещение точки в направлении оси x
равно ____ мм.
Точка
К
деформируемого тела перемещается в
плоскости xoy.
Полное перемещение равно 5 мм.
В направлении оси y
точка переместилась на величину 3 мм.
Перемещение точки в направлении оси x
равно ____ мм.
|
|
|
4 |
Тема: Перемещение и деформация
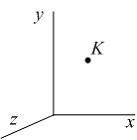
Точка К
деформируемого тела перемещается в
пространстве. Известны полное перемещение
![]() и
перемещения вдоль координатных осей
x,
y
(u
и v).
Величина перемещения вдоль оси z
(w)
определяется по формуле …
и
перемещения вдоль координатных осей
x,
y
(u
и v).
Величина перемещения вдоль оси z
(w)
определяется по формуле …
|
|
|
|
Тема: Перемещение и деформация
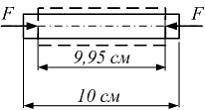 До
приложения к стержню сил F
(см. рисунок)
его длина равнялась 10 см.
После приложения сил F
длина стержня стала равна 9,95 см.
Продольная линейная деформация стержня
равна …
До
приложения к стержню сил F
(см. рисунок)
его длина равнялась 10 см.
После приложения сил F
длина стержня стала равна 9,95 см.
Продольная линейная деформация стержня
равна …
|
|
|
0,005 |

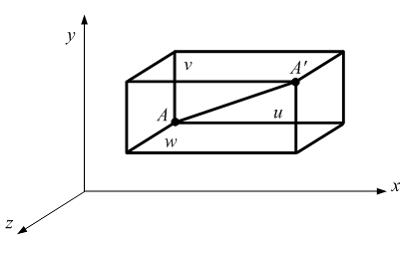 Если
известны перемещения точки A (см. рисунок)
вдоль координатных осей (u, v, w),
то полное перемещение определяется
по формуле …
Если
известны перемещения точки A (см. рисунок)
вдоль координатных осей (u, v, w),
то полное перемещение определяется
по формуле …