8.3. Расчеты на прочность при колебаниях
Коэффициентом динамичности упругой системы при вынужденных колебаниях называется величина, равная … отношению динамического полного перемещения к статическому перемещению в том же сечении ______________________________________________________________________
Промежуток времени между двумя последующими максимальными отклонениями упругой системы от положения статического равновесия называется …
|
|
периодом колебаний |
______________________________________________________________________
Частота
собственных колебаний электродвигателя,
установленного на упругой балке, равна
.
Резонанс наступит при числе оборотов
электродвигателя равном ______
.
|
|
|
______________________________________________________________________
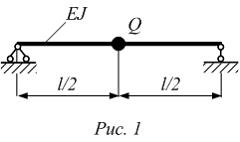Груз
весом Q
расположен в середине пролета балки
длиной l
(рис. 1).
Жесткость поперечного сечения на изгиб
по
длине балки постоянна. Круговая частота
собственных колебаний балки равна …
(Массой балки, по сравнению с массой
груза, пренебречь.)
|
|
|
______________________________________________________________________
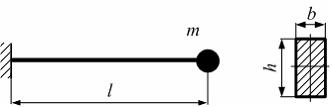На
консольной балке длиной
расположен
груз точечной массой
.
Модуль упругости материала балки Е;
линейные размеры прямоугольного сечения
,
заданы.
При решении задачи массой балки, по
сравнению с массой груза, пренебречь.
Круговая частота собственных колебаний
балки равна …
______________________________________________________________________
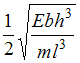Период колебаний Т связан с круговой частотой собственных колебаний системы соотношением …
______________________________________________________________________
Упругая система с грузом массой m и жесткостью с имеет одну степень свободы. Круговая частота собственных колебаний системы равна …
|
|
|
____ Тема: Расчеты на прочность при колебаниях
На
балке установлен электродвигатель (см.
рисунок), в котором имеется несбалансированная
вращающаяся масса. При установившемся
режиме работы условие прочности балки
по допускаемым напряжениям имеет вид
Величина
является
…
|
|
|
максимальным нормальным напряжением в балке от максимального значения возмущающей силы, приложенной статически |
__________________________________________________________________
Числом степеней свободы колеблющейся системы называется …
|
|
количество независимых параметров, однозначно определяющих положение системы в любой момент времени
|
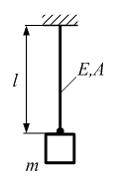Система
состоит из упругого стержня, верхний
конец которого жестко закреплен, а к
нижнему подвешен груз массой m.
Модуль упругости материала стержня Е,
длина l,
площадь поперечного сечения А
заданы. При
увеличении длины стержня в два раза
круговая частота собственных колебаний
системы … Массой стержня пренебречь.
|
|
|
уменьшится в раз |