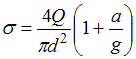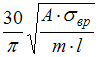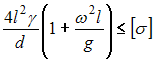- •Введение в курс
- •1.1. Основные понятия, определения, допущения и принципы
- •Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов: 3) упругостью
- •1.2. Модели прочностной надежности
- •1) Стержнем;
- •1.3. Внутренние силы и напряжения
- •1.4. Перемещения и деформация
- •Растяжение и сжатие
- •2.1. Продольная сила. Напряжения и деформации
- •2.2. Испытание конструкционных материалов на растяжение и сжатие
- •2.3. Механические свойства материалов
- •2.4. Расчеты стержней на прочность и жесткость
- •Сдвиг. Кручение
- •3.1. Чистый сдвиг. Расчет на сдвиг (срез)
- •3.2. Крутящий момент. Деформации и напряжения
- •3.3. Расчет на прочность при кручении
- •3.4. Расчет на жесткость при кручении
- •4. Напряженное состояние в точке. Главные площадки и главные напряжения
- •4.2. Виды напряженного состояния
- •4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
- •4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
- •5. Плоский прямой изгиб
- •5.1. Поперечная сила, изгибающий момент и их эпюры
- •5.2. Напряжения в поперечном сечении стержня при плоском изгибе
- •5.3. Расчет балок на прочность
- •5.4. Перемещения при изгибе. Расчет балок на жесткость
- •6.Сложное сопротивление
- •6.1. Виды нагружения стержня
- •6.2. Пространственный и косой изгиб
- •6.3. Изгиб с растяжением-сжатием
- •6.4. Изгиб с кручением
- •7.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина
- •7.2. Статическая неопределимость. Степень статической неопределенности
- •7.3.Метод сил
- •7.4. Расчет простейших статически неопределимых систем
- •8.1. Расчеты на прочность с учетом сил инерции
- •8.2. Прочность при ударных нагрузках
- •Увеличатся в 2 Ответ верный! ______________________________________________________________________
- •8.3. Расчеты на прочность при колебаниях
- •Упругая система с грузом массой m и жесткостью с имеет одну степень свободы. Круговая частота собственных колебаний системы равна …
- •8.4. Расчеты на прочность при напряжениях, периодически меняющихся во времени
- •График пульсационного цикла показан на схеме …
- •9. 1. Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
- •9.2. Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
- •9.3. Влияние условий закрепления концов стержня на величину критической силы
- •9.4. Устойчивость за пределом пропорциональности. Расчет сжатых стержней
- •10.1. Статические моменты. Центр тяжести плоской фигуры
- •10.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
- •5.3. Главные оси и главные моменты инерции
- •10.4. Моменты инерции простых и сложных сечений
8.1. Расчеты на прочность с учетом сил инерции
При определении напряжений в элементах конструкции, точки которых испытывают ускорения, применяют принцип Даламбера, который позволяет динамическую задачу свести к статической, если к внешним силам, действующим на элемент конструкции, добавить силу инерции, равную произведению …
массы тела на ускорение и направленную против ускорения
Ломаный
стержень АВС вращается с
числом оборотов
![]() .
Масса груза, закрепленного в сечении
С, известна:
.
Масса груза, закрепленного в сечении
С, известна:
![]() .
Определите максимальный изгибающий
момент в сечении В стержня.
.
Определите максимальный изгибающий
момент в сечении В стержня.
|
|
![]()
![]()
![]()
![]() ______________________________________________________________________
______________________________________________________________________
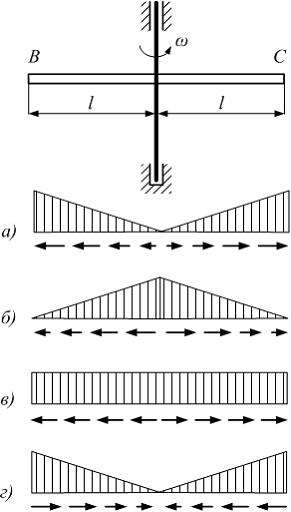 Стержень
ВС
вращается
с постоянной угловой скорость
Стержень
ВС
вращается
с постоянной угловой скорость
![]() вокруг
вертикальной оси. Распределение сил
инерции по длине стержня показано на
схеме …
вокруг
вертикальной оси. Распределение сил
инерции по длине стержня показано на
схеме …
|
|
а
|
______________________________________________________________________ Груз весом Q, подвешенный на тросе, поднимается с постоянным ускорением а. Выражение для определения нормального напряжения в тросе диаметром d без учета его веса имеет вид …
|
|
|
______________________________________________________________________
 Груз
массой m
вращается на проволоке длиной l
вокруг точки О.
Площадь сечения проволоки – А,
предел прочности материала –
Груз
массой m
вращается на проволоке длиной l
вокруг точки О.
Площадь сечения проволоки – А,
предел прочности материала –
![]() .
Число оборотов в минуту, при котором
произойдет разрушение проволоки, равно …
.
Число оборотов в минуту, при котором
произойдет разрушение проволоки, равно …
|
|
|
______________________________________________________________________
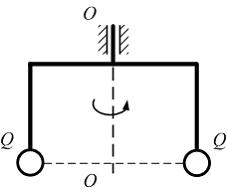 Невесомая
рама с грузами весом
Невесомая
рама с грузами весом
![]() вращается
с постоянной угловой скоростью вокруг
оси
вращается
с постоянной угловой скоростью вокруг
оси
![]() .
Если учитывать только силы инерции, то
опасное сечение рамы работает на …
.
Если учитывать только силы инерции, то
опасное сечение рамы работает на …
чистый изгиб и растяжение Ответ верный!
______________________________________________________________________
Груз
весом Q
поднимается на тросе с постоянным
ускорением
а.
При определении нормального напряжения
в тросе, без учета веса троса, необходимо
учесть силу инерции, которая равна …
![]()
______________________________________________________________________
Груз весом Q подвешен на стальном тросе площадью поперечного сечения А и поднимается с постоянным ускорением а. Объемный вес материала троса (вес единицы объема). Нормальное напряжение в произвольном сечении троса равно …
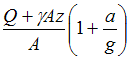
______________________________________________________________________
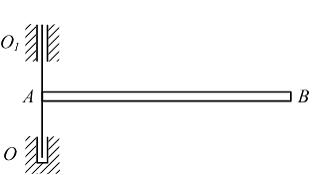 Вал
ОО1 с прикрепленным
к нему стержнем АВ массой т
вращается вокруг своей оси. Максимальное
растягивающее усилие …
Вал
ОО1 с прикрепленным
к нему стержнем АВ массой т
вращается вокруг своей оси. Максимальное
растягивающее усилие …
|
|
возникает в сечении А
|
__________ Тема: Расчеты на прочность с учетом сил инерции
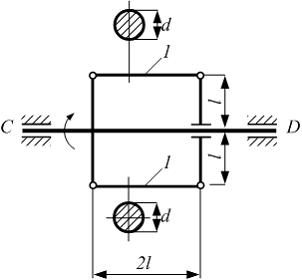 Система,
показанная на рисунке, равномерно
вращается вокруг оси CD
с угловой скоростью
Система,
показанная на рисунке, равномерно
вращается вокруг оси CD
с угловой скоростью
![]() Размер
l,
диаметр d,
допускаемое нормальное напряжение
и
вес единицы объема материала
для
стержней 1 заданы. Условие прочности
для стержней 1 имеет вид …
В расчете
учесть весовую и инерционную нагрузку
на стержни 1.
Размер
l,
диаметр d,
допускаемое нормальное напряжение
и
вес единицы объема материала
для
стержней 1 заданы. Условие прочности
для стержней 1 имеет вид …
В расчете
учесть весовую и инерционную нагрузку
на стержни 1.
|
|
|
|
____ Тема: Расчеты на прочность с учетом сил инерции
Принцип Д΄Аламбера используется в расчетах систем …
|
|
|
движущихся ускоренно |
________________________________________________________
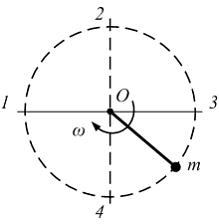 Груз
массой m
прикреплен
проволокой к оси вращения и равномерно
вращается в вертикальной плоскости.
Максимальное значение нормального
напряжения в проволоке будет тогда,
когда груз находится в положении …
Груз
массой m
прикреплен
проволокой к оси вращения и равномерно
вращается в вертикальной плоскости.
Максимальное значение нормального
напряжения в проволоке будет тогда,
когда груз находится в положении …
|
|
|
4 |
Тема: Расчеты на прочность с учетом сил инерции
Если к системе, движущейся ускоренно, кроме активных и реактивных сил приложить силы инерции, то получим уравновешенную систему сил, которая удовлетворяет уравнениям равновесия статики. Данное положение называется принципом …
|
|
|
Д΄Аламбера |