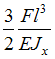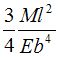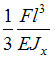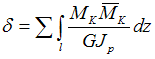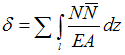- •Введение в курс
- •1.1. Основные понятия, определения, допущения и принципы
- •Задача 1.1.4: Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется… Варианты ответов: 3) упругостью
- •1.2. Модели прочностной надежности
- •1) Стержнем;
- •1.3. Внутренние силы и напряжения
- •1.4. Перемещения и деформация
- •Растяжение и сжатие
- •2.1. Продольная сила. Напряжения и деформации
- •2.2. Испытание конструкционных материалов на растяжение и сжатие
- •2.3. Механические свойства материалов
- •2.4. Расчеты стержней на прочность и жесткость
- •Сдвиг. Кручение
- •3.1. Чистый сдвиг. Расчет на сдвиг (срез)
- •3.2. Крутящий момент. Деформации и напряжения
- •3.3. Расчет на прочность при кручении
- •3.4. Расчет на жесткость при кручении
- •4. Напряженное состояние в точке. Главные площадки и главные напряжения
- •4.2. Виды напряженного состояния
- •4.3. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
- •4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
- •5. Плоский прямой изгиб
- •5.1. Поперечная сила, изгибающий момент и их эпюры
- •5.2. Напряжения в поперечном сечении стержня при плоском изгибе
- •5.3. Расчет балок на прочность
- •5.4. Перемещения при изгибе. Расчет балок на жесткость
- •6.Сложное сопротивление
- •6.1. Виды нагружения стержня
- •6.2. Пространственный и косой изгиб
- •6.3. Изгиб с растяжением-сжатием
- •6.4. Изгиб с кручением
- •7.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина
- •7.2. Статическая неопределимость. Степень статической неопределенности
- •7.3.Метод сил
- •7.4. Расчет простейших статически неопределимых систем
- •8.1. Расчеты на прочность с учетом сил инерции
- •8.2. Прочность при ударных нагрузках
- •Увеличатся в 2 Ответ верный! ______________________________________________________________________
- •8.3. Расчеты на прочность при колебаниях
- •Упругая система с грузом массой m и жесткостью с имеет одну степень свободы. Круговая частота собственных колебаний системы равна …
- •8.4. Расчеты на прочность при напряжениях, периодически меняющихся во времени
- •График пульсационного цикла показан на схеме …
- •9. 1. Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
- •9.2. Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
- •9.3. Влияние условий закрепления концов стержня на величину критической силы
- •9.4. Устойчивость за пределом пропорциональности. Расчет сжатых стержней
- •10.1. Статические моменты. Центр тяжести плоской фигуры
- •10.2. Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей
- •5.3. Главные оси и главные моменты инерции
- •10.4. Моменты инерции простых и сложных сечений
7.1. Определение перемещений с помощью интегралов Мора. Правило Верещагина
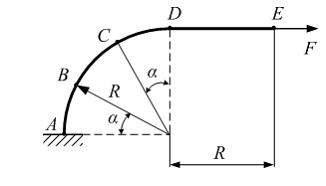
Задача 7.1.1:
Для
представленного на рисунке криволинейного
стержня приведены выражения углов
поворота сечений В,
С,
D,
Е
соответственно. При их определении
учтено только влияние изгибающего
момента. Укажите неправильный ответ,
если
![]() .
.
 Варианты
ответа:
Варианты
ответа:
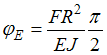 ;
;
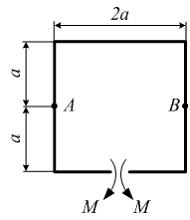
Задача 7.1.2:
Плоская рама
нагружена, как показано на рисунке.
Величины М,
а,
жесткость поперечного сечения на изгиб
![]() заданы.
Взаимное удаление сечений А
и В
равно…
заданы.
Взаимное удаление сечений А
и В
равно…
 Варианты
ответа:
Варианты
ответа:

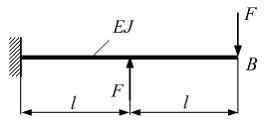
Задача 7.1.3: Жесткость поперечного сечения на изгиб по длине балки постоянна. Размер задан. Значение силы F , при которой прогиб концевого сечения В будет f, равно …
 Варианты
ответа:
Варианты
ответа:
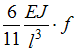
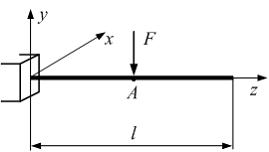
Задача 7.1.4: Для балки, изображенной на рисунке, требуется определить абсолютное перемещение сечения А. Выражение … позволит наиболее точно определить данное перемещение.
 Варианты
ответа:
Варианты
ответа:
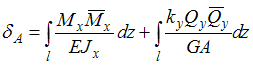 ;
;
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
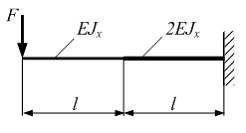 Жесткость
поперечного сечения балки на изгиб на
левом участке
,
на правом –
Жесткость
поперечного сечения балки на изгиб на
левом участке
,
на правом – ![]() .
При нагружении ступенчатой консольной
балки длиной
силой Fзначение
максимального прогиба равно …
(Влиянием поперечной силы на величину
прогиба пренебречь).
.
При нагружении ступенчатой консольной
балки длиной
силой Fзначение
максимального прогиба равно …
(Влиянием поперечной силы на величину
прогиба пренебречь).
|
|
|
|
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
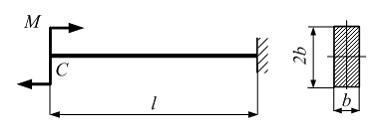 Балка
прямоугольного сечения с размерами b и
2b нагружена
моментом М.
Модуль упругости материала Е,
длина l заданы.
Прогиб концевого сечения балки Спо
абсолютной величине, равен …
Балка
прямоугольного сечения с размерами b и
2b нагружена
моментом М.
Модуль упругости материала Е,
длина l заданы.
Прогиб концевого сечения балки Спо
абсолютной величине, равен …
|
|
|
|
Тема:
Определение перемещений с помощью
интегралов Мора. Правило
Верещагина
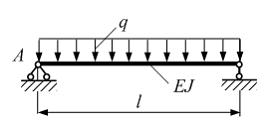 Однопролетная
балка длиной l нагружена
равномерно распределенной нагрузкой
интенсивности q.
Жесткость поперечного сечения на
изгиб
по
длине постоянна. Угол поворота
сечения А равен …
(Влиянием поперечной силы при определении
угла поворота пренебречь).
Однопролетная
балка длиной l нагружена
равномерно распределенной нагрузкой
интенсивности q.
Жесткость поперечного сечения на
изгиб
по
длине постоянна. Угол поворота
сечения А равен …
(Влиянием поперечной силы при определении
угла поворота пренебречь).
|
|
|
|
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
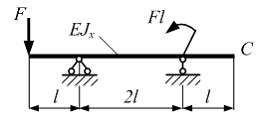
Однопролетная двухконсольная балка нагружена силой и моментом. Жесткость поперечного сечения на изгиб по длине постоянна. Линейный размер lзадан. Прогиб сечения С от внешней нагрузки по абсолютной величине равен… (Влиянием поперечной силы на величину перемещения пренебречь).
|
|
|
|
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
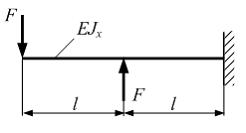
Консольная балка длиной 2l нагружена внешними силами. Жесткость поперечного сечения на изгиб по длине постоянна. Прогиб концевого сечения достигнет величины
|
|
|
|
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
При вычислении интегралов Мора способом Верещагина …
|
|
|
одна из подынтегральной функции должна быть линейной |
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
При плоском изгибе,
без учета поперечных сил, интеграл Мора
вычисляется способом Верещагина по
формуле
![]()
|
|
|
|
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
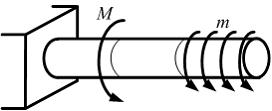 Для
данной расчетной схемы формула интеграла
Мора имеет вид …
Для
данной расчетной схемы формула интеграла
Мора имеет вид …
|
|
|
|
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
Для данной расчетной схемы формула интеграла Мора имеет вид …
|
|
|
|