5.4. Перемещения при изгибе. Расчет балок на жесткость
Задача 5.4.1:
Прогиб на
свободном конце балки
.
Угол поворота поперечного сечения над
опорой
равен…
Варианты
ответа: 24
минутам
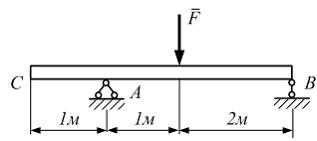
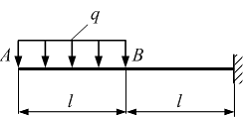
Задача 5.4.2: Консольная балка на участке АВ нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения стержня на изгиб EIz всей длине постоянна. Угол поворота сечения B, по абсолютной величине равен…
Варианты
ответа:
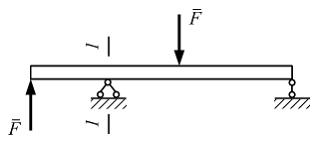
Задача 5.4.3: В поперечном сечении I-I …
Варианты
ответа: -
будет поворот сечения;
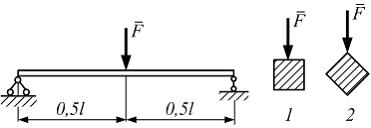
Задача 5.4.4:
Стальная
балка имеет два варианта расположения
квадратного поперечного сечения. В
первом случае она нагружается параллельно
стороне квадрата. Во втором – в
диагональной плоскости. Отношение
прогибов
равно…
Варианты
ответа: 1.
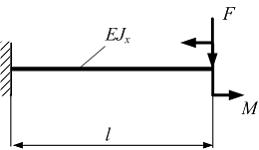
Задача 5.4.5:
Жесткость
поперечного сечения балки на изгиб
по
длине постоянна. Сила
размер
заданы.
Прогиб свободного конца балки равен
нулю, когда значение момента
М равно …
Варианты
ответа:
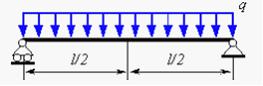
Задача 5.4.6: Балка нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения балки на изгиб по всей длине постоянна и равна EI z. Прогиб в середине пролета балки длиной l равен…
Варианты
ответа:
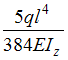
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
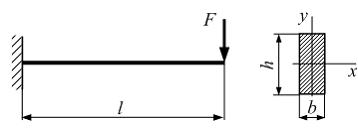Консоль
длиной l нагружена
силой F.
Сечение балки прямоугольное с
размерами b и h.
Модуль упругости материала Е.
При увеличении линейных размеров 
в
два раза значение максимального
прогиба …
|
|
|
уменьшится в 2 раза |
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
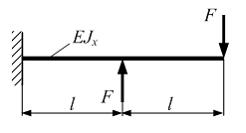Консольная
балка длиной
нагружена
силами F.
Модуль упругости материала Е,
осевой момент инерции сечения 
заданы.
Прогиб концевого сечения примет
значение 
,
когда значение силы F равно …
|
|
|
|
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
Консольная
балка длиной 
нагружена
моментом 
Поперечное
сечение балки прямоугольник: 
Модуль
упругости материала 
Радиус
кривизны балки в сечении I–I равен ___ (м).
|
|
|
3,6 |
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
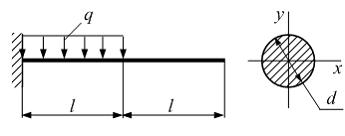Консоль
на половине длины нагружена равномерно
распределенной нагрузкой
интенсивности 
Модуль
упругости материала балки 
размер 
Прогиб
на свободном конце консоли не должен
превышать 
Из
условия жесткости диаметр поперечного
сечения d равен ____ (см).
|
|
|
37,1 |
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
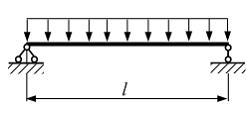Однопролетная
балка длиной l,
высотой h нагружена
равномерно распределенной нагрузкой.
Радиус кривизны нейтрального слоя балки
в середине пролета равен 
. Жесткость
поперечного сечения на изгиб 
по
всей длине постоянна. Максимальное
нормальное напряжение в балке равно …
(Влияние поперечной силы на изменение
кривизны не учитывать).
|
|
|
|
Тема: Перемещения при изгибе. Расчет балок на жесткость
Деревянная балка
прямоугольного сечения шириной
высотой
изогнута
на дуге окружности радиусом 40 м.
Модуль упругости дерева
Максимальное
напряжение в балке равно ____ МПа.
|
|
|
5 |
Тема: Перемещения при изгибе. Расчет балок на жесткость
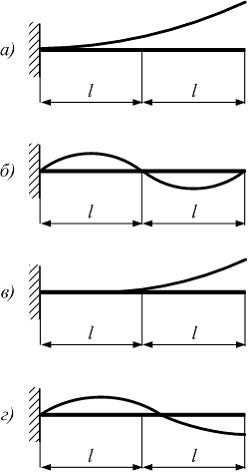Консоль
нагружена внешними моментами. Примерный
вид изогнутой оси балки показан на схеме
…
|
|
|
в |