4.4. Деформированное состояние в точке. Связь между деформациями и напряжениями
Задача 4.4.1: Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название…
Варианты ответа: 4) обобщенного закона Гука.
Задача 4.4.2: Совокупность линейных и угловых деформаций, возникающих по различным осям и в различных плоскостях, проходящих через данную точку тела, называют…
Варианты ответа: 3) деформированным состоянием в точке;
Задача 4.4.3: Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют…
1) главными осями деформированного состояния;
Задача 4.4.4: Модуль упругости материала Е и коэффициент Пуассона μ заданы. Относительное изменение объема равно …
Варианты
ответа:
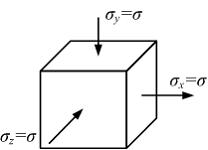
Задача 4.4.5:
На рисунке
показано напряженное состояние в точке
изотропного тела. Модуль упругости
материала
,
коэффициент Пуассона
.
Линейная деформация в направлении оси
х
равна…
Варианты
ответа:
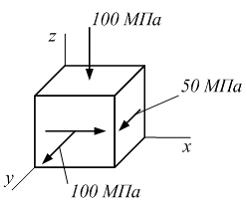
Задача 4.4.6:
Объемный элемент находится под действием
нормальных напряжений, показанных на
рисунке:
,
,
.
Модуль упругости материала
,
коэффициент Пуассона
.
Линейная деформация в направлении оси
z
будет равна нулю, когда
принимает
значение…
Варианты
ответа:
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Для изотропного материала главные оси деформированного состояния совпадают с …
|
|
|
главными осями напряженного состояния |
Тема:
Деформированное состояние в точке.
Связь между деформациями и
напряжениями
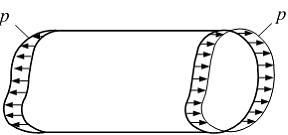Стержень
растянут усилиями, равномерно
распределенными по его торцам
с интенсивностью р. Модуль
упругости Е и
коэффициент Пуассона 
материала
стержня известны. Относительное изменение
объема стержня равно …
|
|
|
|
Тема:
Деформированное состояние в точке.
Связь между деформациями и напряжениями
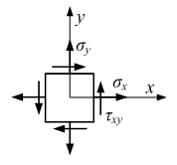Если
величины: 
то
напряжения: 
|
|
|
286, 286, 80 |
Тема:
Деформированное состояние в точке.
Связь между деформациями и
напряжениями
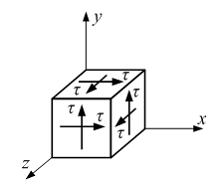Если 
то
линейные деформации: 
|
|
|
0; 0; 0 |
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Число компонент, полностью описывающих деформированное состояние в точке, в общем случае равно …
|
|
|
шести |
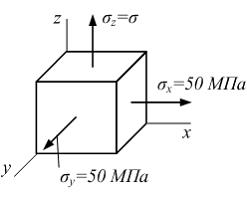
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
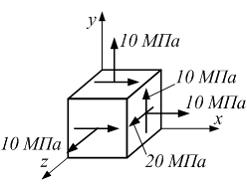На
рисунке показано напряженное состояние
в точке. Модуль сдвига
Угловые
деформации в координатных плоскостях
xy,
yz
и zx
соответственно равны …
|
|
|
|
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
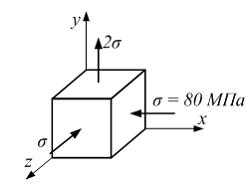На
рисунке показано напряженное состояние
в точке. Известны величины:
Угловые
деформации элементарного параллелепипеда
соответственно
равны …
|
|
|
0; 0; 0 |
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
Деформированное состояние в точке представляет…
|
|
|
тензор |
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
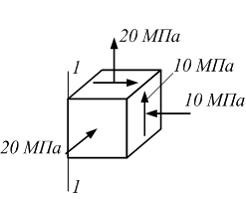На
рисунке показан элементарный параллелепипед
и напряжения на его гранях. Модуль
упругости
,
коэффициент Пуассона
.
Деформация в направлении 1-1 равна …
|
|
|
|
