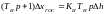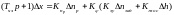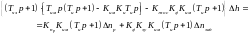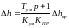2.2. Разработка функциональной схемы системы автоматического регулирования и формирование ее математической модели

На основании полученного уравнения динамики ГД и выбранного регулятора частоты вращения «Вудворд» UG – 8 построим функциональную схему САР.

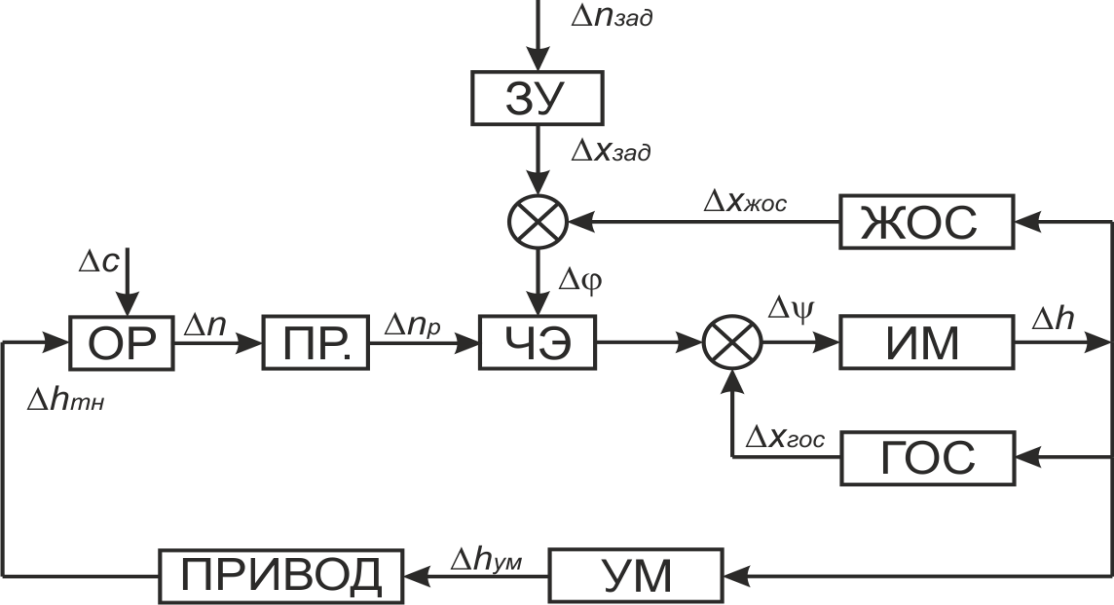
Рис. 10 Функциональная схема САР.

Для составления математической модели системы автоматического регулирования запишем следующие уравнения узлов регулятора и уравнение главного двигателя

	объект регулирования	(20)
	чувствительный элемент	(21)
	исполнительный механизм	(22)
	жесткая обратная связь	(23)
	гибкая обратная связь	(24)
	задающее устройство	(25)
	сумматоры	(26)
		(27)
	УМ с приводом ТНВД	(28)
	привод регулятора	(29)

2.2.1 Вывод уравнения динамики сар

Для вывода общего уравнения динамики воспользуемся полученными выше уравнениями для всех элементов. Методом исключения промежуточных фазовых переменных величин преобразуем систему уравнений (20) - (29) к единому дифференциальному уравнению динамики системы автоматического регулирования в целом.

Подставим выражения (23) н (25) в уравнение (61), а затем видоизмененное последнее в уравнение (21). Тогда уравнение динамики измерительного устройства регулятора принимает вид:

(30)

Из уравнения (24) определим

(31)

а из (22)

(32)

Подставив выражения (31) и (32) в равенство (27), получим общее уравнение ИМ, ГОС и связывающего их сумматора:

(33)

После этого подставим выражение (33) в уравнение динамики измерительного устройства регулятора (30):

(34)

Преобразовав выражение (34), получим уравнение динамики автоматического регулятора в виде

(35)

Из уравнения (28) получим

(36)

Подставив выражения (29) и (36) в уравнение (35), будем иметь

(37)

Из уравнения (20) ОР находим

(38)

Условие замыкания

Подставив уравнение (38) в (37), получим дифференциальное уравнение динамики замкнутого контура автоматического регулирования в операторной форме следующего вида

(39)

После преобразований получим общее уравнение САР:

(40)

2.2.2. Статика регулятора и выбор его параметров

Уравнение динамики (35) регулятора в целом дает возможность сделать ряд важных выводов в части его статических свойств и особенностей как автономно рассматриваемого устройства. Формально, при выполнении условия p= 0, это уравнение порождает уравнение статического равновесия регулятора в виде

Отсюда

или

(41)

Здесь будем считать, что

	(42)
	(43)

где К_р и К_зад – коэффициенты усиления регулятора в целом соответственно по частоте вращения его приводного вала и каналу задания скоростного режима, инд/(об/мин)_р и инд/ед изм ЗУ