17.Структура решений линейных однородных и неоднородных ду n-го порядка.

ДУ наз линейным ДУ п-го порядка.

Рассм линейный диф-ый оператор 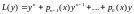. Этот оператор обладает след св-ми:1) постоянный множитель можно вынести за знак оператора. 2) Оператор от суммы 2-х ф-й равен сумме опер от этих ф-й. 3) (3)

- ЛНДУ

- ЛОДУ

Ф-я явл-ся реш-ем ЛНДУ на , если оператор .

Ф-я явл-ся реш-ем ЛОДУ, если

1) Лоду

Опр. Совокупность п-реш-й ЛОДУ (1), опр-ых и л.н на , наз ФСР на .

Для того чтобы с-ма п-реш-ий была фундаментальной необх и дост, чтобы 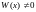этих реш-ий хотя бы в одной точке промежутка непр-ти коэф ур-я (1)

Теор. Если коэф ур-я (1) непр-ны на , то сущ-ет ФСР, опр-ных на .

►Пусть . Решения ур-я (1)сущ-ют по т-ме Пикара. Построим это реш-е. Пусть 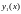-реш-е, удовл след нач усл-ям :

……………….

зн, - л.н,т.е обр-ют ФС. ◄

Теор. Если - ФСР ур-я (1) с непр. Коэф, ф-ла 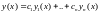(2), где С-константы,дает общее реш-е ур-я (1) в области задания ур-я (1)

►В силу т-мы Пикара и св-в линейного оператора у(х), опр-мая ф-лой (2), явл-ся реш-ем ур-я (1). Это реш-е будет общим , если возможно опр-ть произвольные постоянные Ск. Т.о, чтобы выполнялись произвольно заданные нач усл-я . Пусть удовл этим нач усл-ям. Тогда мы имеем с-му п-линейных ур-ий относительно Ск.

……………..

Неодн с-ма линейных ур-ий относит Ск. явл-ся опр-лем этой с-мы.

В силу т-мы Кронекера-Капели, эта с-ма имеет единств реш-е. .◄

2)ЛНДУ

Рассм. L[y] = y⁽ⁿ⁾ + p_n-1(x)y^(n-1) + … + p₁(x)y' + p₀(x)y = f(x) (1), где р_k(x), k={1, …, n-1}, f(x) – непрер. ф-ции на некотором промежутке I = [a,b]. Предположим, что у₀(х) – некот. частное решение (1).

Теор. Общее решение ЛНДУ имеет вид 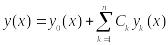(2), где y₀ – некот. частное решение (1), а 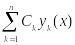- общее решение соотв. однородного ур-ия (5). [(5) = L[y] = 0].

►L[y] = L[y₀] + = f(x) + 0 = f(x) => (2) удовл. ур-ию (1). С др. стороны, если у(х) – любое решение ур-ия (1), то L[y - y₀]=L[y] - L[y₀] = f(x) – f(x) = 0 => y-y₀ – решение ЛОДУ. Тогда ƎС_k: y(x) – y₀(x) = => .◄

Теор. Пусть у₁(х) – частное решение уравнения L[y] = f₁(x), у₂(х) – частное решение уравнения L[y] = f₂(x). Тогда у₁(х) + у₂(х) – некоторое частное решение уравнения L[y] = f₁(x) + f₂(x).

►L[y₁+y₂] = L[y₁] + L[y₂] = f₁(x) + f₂(x) – по св-ву линейного оператора.◄

Теор. Если L[y] = U(x) + iV(x), где коэф. p_k(x), k = {0, …, n-1} и ф-ции в U(x) и V(x) действит., имеет решение у(х) = u(x) + iv(x), то действит. часть u(x) и мнимая часть v(x) решения явл. решениями соотв. ур-ий L[y]=U(x), L[y]=V(x).

►Основана линейности оператора L[y].◄

18.Формула Остроградского-Лиувилля.

Для линейного ДУ L[y]=0 c непрер. коэф. имеет место формула 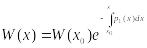(1), где р₁(х) – коэф. при у^(n-1)(x), W(x) – определитель Вронского ФСР.

►Докажем эту формулу для ДУ 2-го порядка: у'' + р₁(х)у'(х) + р₀(х) (2). 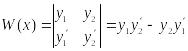, где у₁ и у₂ решения ДУ (2). Найдём W'(x):

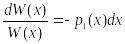
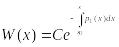x = x₀, C = W(x₀)◄

Из формулы Остроградского-Лиувилля следует любое решение ур-ия (2) явл. решением | ∙ . .

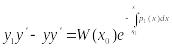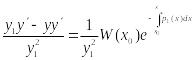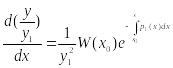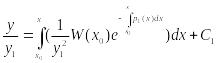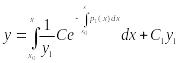. . (3) - формула для нахождения решения ЛОДУ 2-го порядка, если одно решение известно.