8.Однородные ду 1-го порядка.

Рассмотр. ДУ М(х,у)dx + N(x,y)dy = 0 (1).

Опр.Ф-ция f(x,y) наз. однородной ф-ей степени m, если t имеет место равенство: f(tx, ty) = t^m∙ f(x,y) (2).

Положим в (2) t = , тогда f(1, ) = ∙ f(x,y). f(x,y) = x^m ∙ f(1, ) (3).

Опр. ДУ (1) наз. однородным, если М(х,у) и N(x,y) однородные ф-ции одной и той же степени m.

Преобраз. (1) иначе: . В силу (3) это = 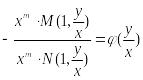(4). Получаем: 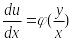(5). Из (5) => однород. ур-ия в нач. коорд. вообще говоря не задаёт определённого направления поля, т.к. ч/з начало координат не проходит ни одна интегр. кривая. Интегр. кривые однород. ур-ия могут лишь примыкать к началу координат.

Для того чтобы проинтегр. однородное ур-ие (1) сделаем замену перемен. y=zx, где z – новая искомая ф-ция от х. Имеем: М(х, zx)dx + N(x, zx)(zdx + xdz) = 0. Т.к. М(х, у) = x^m ∙ М(1, ) , N(x,y) = x^m ∙ N (1, ), то М(х, zx) = x^m ∙ М(1, z) , N(x, zx) = x^m ∙ N (1, z). Тогда x^m ∙ М(1, z)dx + x^m ∙ N (1, z)(zdx + xdz) = 0. (M(1, z) + zN(1, z))dx + xN(1, z)dz = 0 – ур-ие с разд. перемен. Разделяя их будет: , С = С₁ - решение.

Зам. Разделяя переменные можно потерять решение вида z = a, где а – корень ур-ия M(1, z) + zN(1, z) = 0. Отсюда сразу => у = ах. Эти решения могут содержаться в формуле общего интегр., но м.б. и особыми. Особыми решениями м.б. также полуоси х = 0.

Обобщ. однородные ур-ия

Ур-ие М(х,у)dx + N(x,y)dy = 0 (6) наз. обобщённым однородным ур-ем, если Ǝk: левая часть уравнения становится однородной ф-ей от величин x, y, dx, dy, при условии что они считаются величинами соответственно первого, k-ого, нулевого и (k-1) измерения, т.е. если ур-ие имеет вид: M(tx, t^ky)dx + N(tx, t^ky)t^k-1dy = 0, t^m(M(x,y)dx+N(x,y)dy)=0, M(tx, t^ky)dx + N(tx, t^ky)t^k-1dy = t^m(M(x,y)dx+N(x,y)dy) = 0, M(tx, t^ky)dx + N(tx, t^ky)t^k-1dy = t^m(M(x,y)dx+N(x,y)dy) (7). M(tx, t^ky) = t^m(M(x,y); N(tx, t^ky) = t^m-(k-1)N(x,y) (8). При k = 1 получ. общее однородное ур-ие.м

Если положить, что y = zx^k, то ур-ие (6) с новой переменной z приводится к ур-ию с раздел. переменными. dy = zkx^k-1dx + x^kdz.

Положим t = , тогда в (8): => . => . M(x, zx^k) = x^mM(1, z) и N(x, zx^k) = x^m-k+1N(1, z) подставим в (1): . .| x = 0 –?. - ур-ие с раздел. переменными.

9.Линейные ду 1-го порядка. Линейные однородные ду 1-го порядка.

M(x,y)dx + N(x,y)dy = 0 (1) является линейным ДУ, если оно линейно относительно искомых ф-ций. Если искомая функция у, то (1) линейно относительно у: у' = -р(х)у+g(x) (2). Если в (2) g(x) = 0, то у'+р(х)у = 0 (3) – линейное однородное ДУ.

Будем считать ф-ции p(x), g(x) непрер. на некотором промежутке I. Из теор. Пикара => (2) имеет единств. решение у = у(х) удовл. начальным усл. у(х₀)=у₀, у₀ϵI, его можно выбирать произвольно. Т.е. через каждую (.) (х₀,у₀) проходит единств. интегральная кривая уравнения (2).

Покажим, что (2) всегда интегр. в квадратурах, р(х) – непрер. ф-ция. у'+р(х)у = 0 | y = 0? .

Решение у=0 содержится в общем решении при С=0.

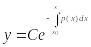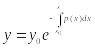Покажим, что (4) явл. общим решением (3) в области I=(a,b), . Действительно, у разрешено относительно С: , где ф-ция С определена на . Кроме того, по построению (4) явл. решением (3) в интервале (a,b) при всех знач. произвол. постоянных С. Заменив неопредел. интеграл определённым: (5). Положив х₀ = х и обозначив у(х₀) = у₀ и тогда решение получим: , если у₀ – произвол., то это общее р-ие, если у₀ – фиксир., то это частное решение линейного однородного ДУ.